As razões trigonométricas de um ângulo são as razões obtidas dos três lados de um triângulo retângulo. Em outras palavras, esses são os valores que resultam da comparação de seus três lados por meio de quocientes (divisões). Embora deva ser destacado que essas razões só existem em triângulos retângulos (triângulos que possuem um ângulo de 90º).
Razões trigonométricas em um triângulo retângulo
As seis razões trigonométricas mais importantes são: seno, cosseno, tangente, cossecante, secante e cotangente. A seguir explicaremos detalhadamente como se define cada um desses motivos e falaremos sobre a fórmula que os caracteriza. Para entender as seguintes explicações, levaremos em consideração o seguinte triângulo retângulo:

Seios
O seno de um ângulo (sin ou sin) é igual ao quociente do cateto oposto (a) entre a hipotenusa (c), portanto, a fórmula do seno é: sin (α) = a/c . É muito importante conhecer esta definição de seno, porque ela é a base de toda trigonometria, juntamente com as outras razões que abordaremos nesta seção.
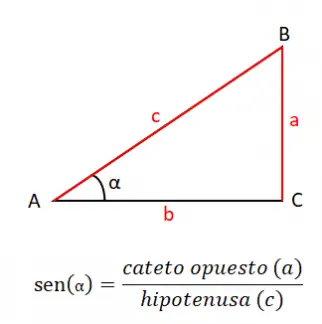
Trav É a partir do teorema do seno que podemos calcular qualquer lado do triângulo , podemos fazer isso ligando os quocientes de um determinado ângulo entre o seu lado correspondente. Por exemplo, se quisermos calcular o lado a e tivermos os valores dos lados pelos ângulos A e B, podemos fazê-lo usando a fórmula: a / sin (A) = b / sin (B) . Resolvendo esta equação simples, obtemos o valor correspondente à variável que queremos calcular.
Cosseno
O cosseno de um ângulo (cos) é igual ao quociente do cateto adjacente (b) entre a hipotenusa (c), portanto, a fórmula do cosseno é: cos (α) = b/c . Neste caso, a fórmula é composta pelos dois lados do triângulo que estão em contato com o ângulo que queremos estudar, neste exemplo, o ângulo A ou α.
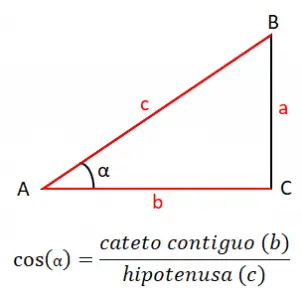
Com o cosseno, também temos uma forma de calcular os lados do triângulo , que vem do teorema do cosseno. Isso nos permite conectar os lados aos ângulos e nos dá as três expressões a seguir:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Tangente
A terceira razão mais importante, com a qual fecharemos o conjunto de razões originais, é a tangente (tan ou tg). Isso é calculado dividindo-se entre a perna oposta (a) e a perna adjacente (b), portanto a fórmula da tangente é: tan (α) = a / b . Você pode ver isso graficamente abaixo:
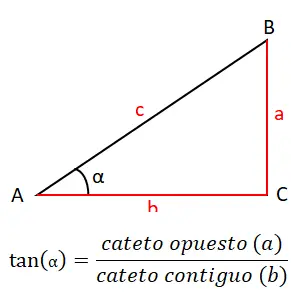
A tangente também possui seu próprio teorema, denominado teorema da tangente. Isto permite-nos relacionar os comprimentos de dois lados de um triângulo com as tangentes dos ângulos . A afirmação é a seguinte: “o quociente da soma de dois lados entre a sua subtração é igual ao quociente entre a tangente da média dos dois ângulos opostos a esses lados e a tangente da metade da diferença destes”.
Razões trigonométricas derivadas
A partir das três razões trigonométricas que acabamos de discutir, podemos obter outras razões trigonométricas derivadas. Estes são obtidos tomando a razão inversa em relação ao seno, cosseno e tangente.
- Cossecante: é a razão inversa do seno e é calculada com as fórmulas: cosec (α) = c / a e cosec (α) = 1 / sin (α).
- Secante: é a razão inversa do cosseno e é calculada com as fórmulas: sec (α) = c/b e sec (α) = 1 / cos (α).
- Cotangente: é a razão inversa da tangente e é calculada com as fórmulas: cotg (α) = b / a e cotg (α) = 1 / tan (α).
Tabela de razões trigonométricas
Abaixo você confere uma tabela que resume todos os motivos explicados até agora. Com esta tabela você poderá memorizar todas as fórmulas de forma eficaz, pois permite distinguir facilmente as diferenças entre cada expressão matemática.
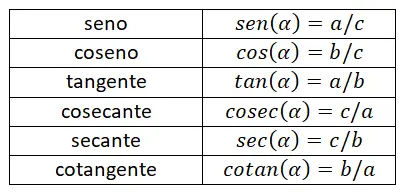
Razões trigonométricas em um círculo
Outra forma de estudar trigonometria é através da circunferência goniométrica ou círculo unitário , esta circunferência tem raio igual a 1 e sua origem é o ponto (0, 0). O desenho consiste em um círculo e um triângulo retângulo representados dentro do círculo, mais precisamente, o ângulo que vamos estudar deve tocar o ponto original.
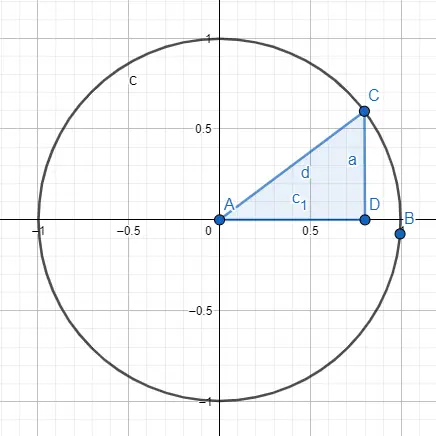
Quando temos esta imagem, sabemos que o raio é igual à hipotenusa, que é igual a 1. Então se quisermos calcular o seno e o cosseno, usaremos o valor do raio e o valor dos outros lados de O triângulo. Para calcular o seno, faremos o seguinte cálculo: sin (A) = CD / AC = CD / raio = CD / 1 = CD , então o seno de A é a. Por outro lado, para calcular o cosseno, faremos o cálculo: cos (A) = AD / AC = AD / raio = AD / 1 = AD , portanto o cosseno de A é c1.
É muito importante ter duas coisas em mente. A primeira é que a utilização deste círculo no estudo das razões trigonométricas se deve à necessidade de lidar com ângulos maiores do que aqueles que podem ser estudados com o triângulo. Por exemplo, o ângulo de 150º não pode ser estudado através de um simples triângulo, porque é muito grande. E a segunda coisa a ter em mente é que seno e cosseno nunca podem adotar valores maiores que 1 e menores que -1.
Sinal de razões trigonométricas
Como dissemos antes, para lidar com ângulos maiores do que um triângulo nos permite, utilizamos a circunferência goniométrica. Para isso representamos um triângulo dentro do círculo exatamente em um dos quatro quadrantes que dividem a circunferência, na imagem a seguir você pode ver os quatro quadrantes representados.
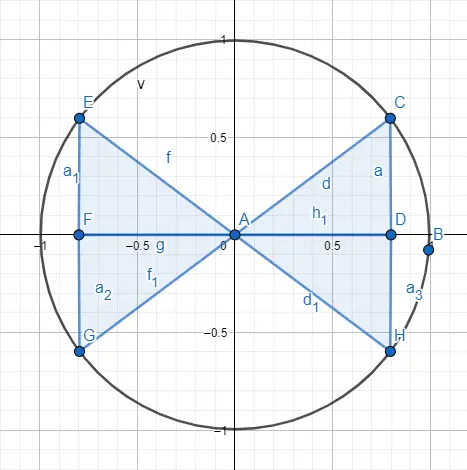
Então, para distinguir entre um ângulo de 30 e um de 210, que se tornam iguais em relação à distribuição dentro do triângulo , utilizaremos uma distribuição de sinais de acordo com o quadrante em que o triângulo está localizado. Abaixo você pode ver os sinais correspondentes a cada quadrante e um exemplo desenhado.
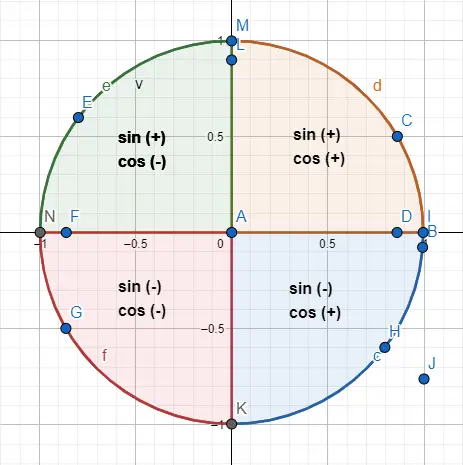
Por exemplo, os ângulos 30º e 210º partilham o mesmo valor numérico , mas o seu seno e cosseno têm sinais opostos. Então: sin(30) = 1/2 e cos(30) = √3/2, enquanto sin(210) = -1/2 e cos(210) = -√3/2. Para chegar a este resultado representamos os dois ângulos da circunferência (imagem abaixo) e seguimos as indicações dos sinais.
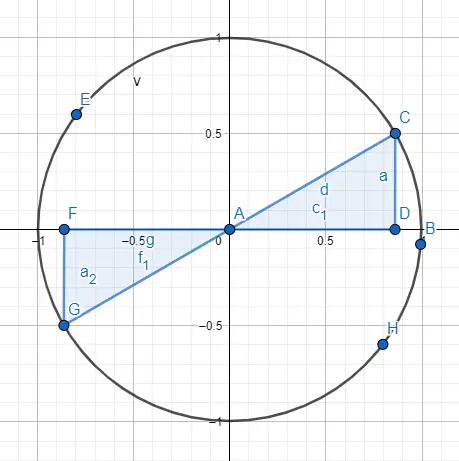
Por fim, como é possível ter ângulos maiores que 360º , embora possa não parecer porque a circunferência é de apenas 360º. Mas, se quisermos resolver um ângulo de 750º, podemos reduzir para um ângulo entre 0º e 360º. Simplesmente dividimos 750 por 360 e o restante é o ângulo restante, no caso de 750º obtemos um ângulo de 30º.
Tipos de ângulos dependendo do quadrante
Existem relações entre diferentes ângulos, o que nos permite calcular as proporções valores trigonométricos de todos os ângulos pertencentes ao círculo. Vamos entender essas razões da redução ao primeiro quadrante . Isto significa que fazemos uma simplificação de um determinado ângulo para o primeiro quadrante e depois aplicamos os sinais correspondentes. Abaixo você encontrará os diferentes procedimentos explicados (dependendo do quadrante):
primeiro quadrante
Neste primeiro quadrante (0º – 90º), só temos que resolver a razão trigonométrica com o ângulo que nos é dado. E se olharmos para a imagem que explicamos anteriormente sobre os símbolos, o seno e o cosseno têm um positivo na frente deles (o resultado que obtivermos não será afetado pelo sinal).
Redução do segundo quadrante para o primeiro
No segundo quadrante (90º – 180º) estamos lidando com ângulos suplementares, o que significa que a soma dos dois ângulos dá 180º. Portanto, precisamos fazer uma redução do segundo quadrante para o primeiro e fazemos isso com a fórmula 180 – α = β , onde α é o ângulo do primeiro quadrante e β é o ângulo original.
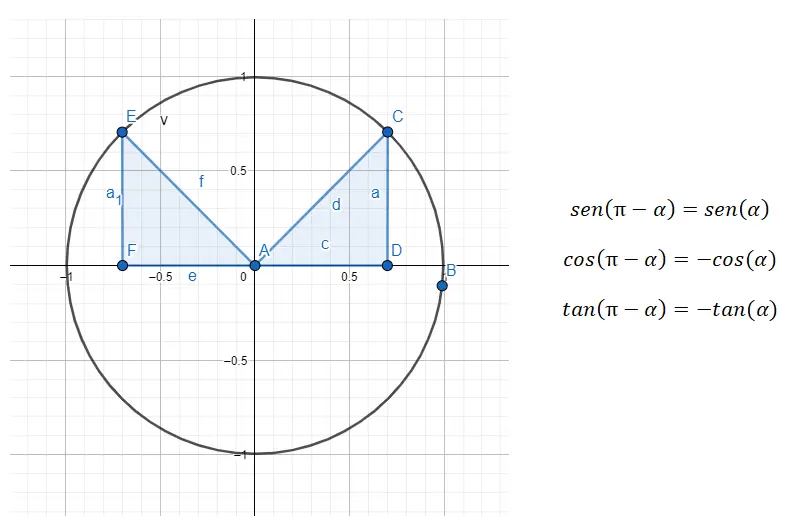
Por exemplo, se nos for dado o ângulo 135º (que pertence ao segundo quadrante), precisamos encontrar o ângulo do primeiro quadrante que está relacionado a este primeiro. Neste exemplo, o ângulo (α) que procuramos é 45º, pois 180 – 45 = 135. Então, isso será verdade: sin (135) = sin (180 – 45) = sin (45), cos (135 ) = cos (180 – 45) = -cos (45) e tan (135) = tan (180 – 45) = -tan (45).
Redução do terceiro quadrante ao primeiro
No terceiro quadrante (180º – 270º) , estamos lidando com ângulos que diferem em 80º, o que significa que os ângulos estão separados por 180º. Então se quisermos reduzir do terceiro quadrante para o primeiro, precisamos usar a fórmula 180 + α = β , onde α é o ângulo do primeiro quadrante e β é o ângulo original.
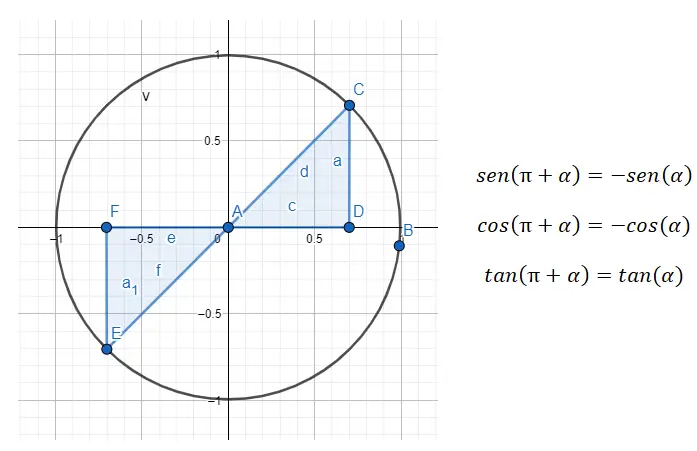
Por exemplo, se nos for dado o ângulo 225º (que pertence ao terceiro quadrante), precisamos de encontrar o ângulo do primeiro quadrante que lhe corresponde. No caso de 225º, o ângulo (α) que procuramos é novamente 45º, pois 180 + 45 = 225. Então, sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) e tan (225) = tan (180 + 45) = tan (45) serão satisfeitos. ).
Redução do quarto quadrante para o primeiro
No quarto quadrante (270º – 360º) estamos lidando com ângulos opostos, o que significa que os ângulos são numericamente iguais, mas de sinais opostos , como 30º e -30º (equivalente a 330º, já que 360º – 30º = 330º) . É importante ter em mente que ângulos opostos podem ser escritos como um ângulo positivo e um ângulo negativo ou como dois ângulos positivos (no exemplo que acabamos de discutir, explicamos a diferença).
Então se quisermos fazer uma redução do quarto quadrante para o primeiro, precisamos usar a fórmula 360 – α = β , onde α é o ângulo do primeiro quadrante e β é o ângulo original.
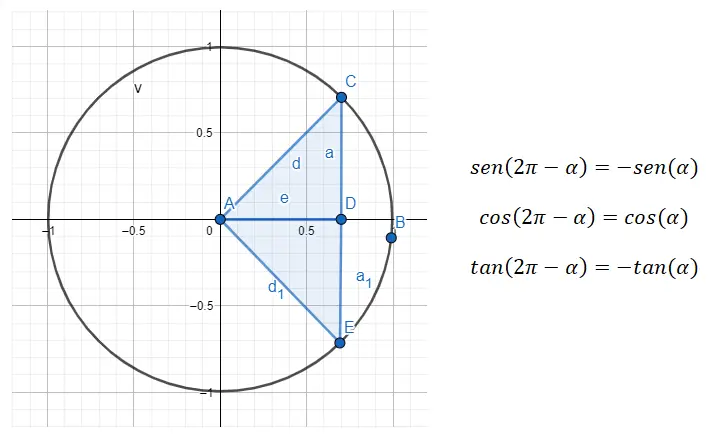
Por exemplo, se nos for dado o ângulo 315º (que pertence ao quarto quadrante), precisamos primeiro encontrar o ângulo do primeiro quadrante que está relacionado a este. No caso do ângulo (α) que procuramos, ainda é 45º, pois, 360 – 45 = 315. Então, sin (315) = sin (360 – 45) = -sin (45), cos (315 ) = cos (360 – 45) = cos (45) e tan (315) = tan (360 – 45) = -tan (45). Concluindo, vimos os ângulos derivados de 45º de todos os quadrantes.
Razões trigonométricas dos ângulos mais importantes
Existem vários ângulos, chamados ângulos notáveis , que são mais comuns em trigonometria. É altamente recomendável saber de cor suas razões trigonométricas. Portanto, a seguir criamos uma tabela contendo as razões trigonométricas desses ângulos e suas derivadas (mesmos ângulos, mas com diferença de 90, 180 ou 270 graus):
| Ângulo (°) | Ângulo (rad) | Seios | Cosseno | Tangente |
| 0º | 0 radical | 0 | 1 | 0 |
| 30º | 1/6 πrad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60º | 1/3 πrad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 πrad | -√2/2 | √2/2 | -1 |
Relação entre razões trigonométricas
Existem várias maneiras de relacionar as diferentes razões trigonométricas. A partir dessas relações, obtemos uma espécie de igualdade entre as diferentes funções trigonométricas, que chamamos de identidades trigonométricas. Graças a este tipo de identidades podemos calcular uma proporção com base em qualquer outra. Deve-se notar que existem muitos tipos diferentes de identidades trigonométricas, que são classificadas com base no tipo de relacionamento que sustenta a própria expressão.
Problemas resolvidos de razões trigonométricas
A seguir, oferecemos uma série de exercícios com os quais você poderá colocar em prática toda a teoria explicada neste artigo. Lembre-se que se em algum momento você tiver dúvidas ou dúvidas, pode reler o artigo e com certeza, com uma segunda leitura , entenderá tudo muito melhor. Dito isto, você pode começar a praticar:
Exercício 1
Calcule as seis razões trigonométricas do ângulo 225º:
Começaremos calculando o ângulo (α), que é igual a: 180 + α = 225º, portanto α = 45º.
pecado (225) = pecado (180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
bronzeado(225) = bronzeado(180 + 45) = bronzeado(45) = 1
Exercício 2
Calcule as seis razões trigonométricas do ângulo 120º:
Começaremos calculando o ângulo (α), que é igual a: 180 – α = 120º, portanto α = 60º.
pecado (120) = pecado (180 – 60) = pecado (60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
bronzeado(120) = bronzeado(180 – 60) = -tan(60) = -√3
Exercício 3
Calcule as seis razões trigonométricas do ângulo 510º:
Antes de começar, deve-se fazer a redução do ângulo: 510/360 = 1 volta e resta um ângulo de 150. A seguir calculamos o ângulo (α), que é igual a: 180 – α = 150, portanto α = 30º.
pecado (150) = pecado (180 – 30) = pecado (30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
bronzeado(150) = bronzeado(180 – 30) = -tan(30) = -√3/3