Nesta página você descobrirá o que são as raízes de um polinômio e como elas são calculadas. Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo nas raízes de um polinômio.
Quais são as raízes de um polinômio?
Em matemática, as raízes (ou zeros) de um polinômio são os valores que cancelam o polinômio. Ou seja, as raízes de um polinômio são todos aqueles valores que, quando avaliados no polinômio, possuem valor numérico igual a 0.
Eventualmente,
![]()
é uma raiz do polinômio
![]()
Sim
![]()
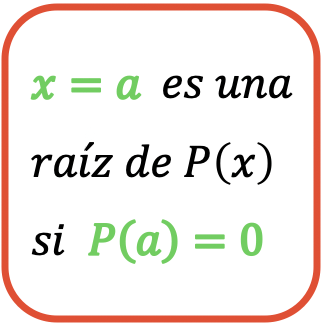
Por exemplo, se tivermos o seguinte polinômio:
![]()
Podemos verificar que uma das raízes do polinômio é 1, pois o valor numérico do polinômio em x=1 é igual a zero:
![]()
Por outro lado, 3 não é raiz do polinômio porque não é um valor que anula o polinômio, ou seja, o valor numérico do polinômio em x=3 é diferente de zero:
![]()
Você provavelmente agora entende melhor o que é a raiz de um polinômio, mas não gostaria de saber quantas raízes um polinômio tem? Ou como encontrar todas as raízes de um polinômio? Bem, é exatamente isso que veremos na próxima seção.
Como calcular todas as raízes de um polinômio?
Para encontrar todas as raízes de um polinômio, você deve seguir os seguintes passos:
- Primeiro, todos os divisores do termo independente do polinômio são calculados.
- Segundo, todos os valores encontrados na etapa anterior são avaliados no polinômio.
- Por fim, se ao avaliar um número no polinômio seu valor numérico for igual a zero, esse número é raiz do polinômio. Caso contrário, o referido número não corresponde à raiz do polinômio.
Este procedimento é deduzido do teorema do resto , clique neste link para descobrir o motivo deste procedimento específico.
Exemplo de cálculo das raízes de um polinômio
A seguir resolveremos um exemplo passo a passo para que você entenda melhor como tirar as raízes de um polinômio.
- Quais são todas as raízes do seguinte polinômio?
![]()
Em primeiro lugar, devemos encontrar os divisores do termo independente, pois toda raiz de um polinômio é também um divisor do termo independente. Então, os divisores de 6 são:
Divisores de 6: +1, -1, +2, -2, +3, -3
Lembre-se que se um número é um divisor, seu negativo também é um divisor. Como um número é divisível por números positivos e negativos.
Assim, as possíveis raízes ou zeros do polinômio são: ±1, ±2, ±3. Portanto, precisamos determinar o valor numérico do polinômio para todos esses valores. E, para isso, substituímos esses valores na expressão do polinômio onde existe um x:
![]()
![]()
![]()
![]()
![]()
![]()
Então o polinômio só desaparece quando a variável x é +2 ou +3, então aqui estão as raízes do polinômio:
Raízes ou zeros do polinômio : +2 e +3
Por outro lado, observe que o polinômio tem tantas raízes quanto o seu grau, ou seja, como o polinômio é de segundo grau, ele tem duas raízes. Nas propriedades das raízes de um polinômio (abaixo), veremos porque essa característica sempre vale para qualquer polinômio.
Acabamos de ver uma maneira de determinar as raízes de um polinômio. No entanto, ainda existem outros métodos para conseguir isso, por exemplo, você também pode encontrar as raízes de um polinômio com a regra de Ruffini. Clique no link a seguir para ver exemplos da regra de Ruffini , aqui você descobrirá em que consiste esse conhecido método e, também, quais as diferenças entre os dois procedimentos.
Propriedades das raízes de um polinômio
As raízes ou zeros de um polinômio possuem as seguintes características:
- Como vimos anteriormente, as raízes inteiras (ou zeros) de um polinômio são divisores do termo independente do polinômio.
- Se conhecermos todas as raízes de um polinômio, podemos expressar esse polinômio na forma de produtos de binômios do tipo
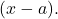
Por exemplo, o polinômio
![]()
Possui 3 raízes que são
![]()
E
![]()
Podemos, portanto, reescrever o polinômio na forma de 3 multiplicações de fatores, cada uma formada pela variável
![]()
e uma raiz mudou de sinal:
![Rendered by QuickLaTeX.com \displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce071610927d2723c8ac2e7b299c1c5d_l3.png)
![]()
Isso é chamado de fatoração polinomial. Na verdade, uma das principais aplicações da determinação das raízes de um polinômio é que elas são usadas para fatorá-lo. No link a seguir você poderá descobrir em que consiste essa operação tão especial e, além disso, poderá praticar com exercícios resolvidos de fatoração polinomial .
- Um polinômio tem tantas raízes quanto seu grau indica. Portanto, um polinômio de segundo grau terá 2 raízes, um polinômio de terceiro grau terá 3 raízes, um polinômio de quarto grau terá 4 raízes e assim por diante.
- Se um polinômio não possui um termo independente, significa que uma de suas raízes é 0. Então as demais raízes devem ser divisores do coeficiente do monômio de menor grau.
Por exemplo, o seguinte polinômio não possui termo independente:
![]()
Portanto, uma raiz do polinômio deve necessariamente ser 0. E o restante das raízes são divisores do coeficiente do termo de grau mais baixo, ou seja, -2. Mais precisamente, as outras raízes são
![]()
E
![]()
então todas as raízes do polinômio são:
Raízes ou zeros do polinômio: 0, +1 e -2
- Quando as raízes de um polinômio não podem ser determinadas, diz-se que é um polinômio irredutível.
Por exemplo, tentaremos calcular as raízes do seguinte polinômio:
![]()
As únicas raízes possíveis do polinômio são os divisores de -1, ou seja -1 e +1. Portanto, avaliamos o polinômio com estes valores:
![]()
![]()
Em nenhum caso o polinômio é cancelado, portanto não possui raízes e, portanto, é um polinômio irredutível.
- Quando o polinômio é composto pelo produto de vários polinômios, não é necessário fazer este produto para calcular as raízes, mas as raízes do polinômio são as raízes de cada fator multiplicadas.
Por exemplo, se tivermos o seguinte polinômio:
![]()
Da segunda propriedade das raízes dos polinômios, podemos deduzir que a raiz do polinômio esquerdo é +2 e a raiz do polinômio direito é -1.
![]()
![]()
Assim, as raízes do polinômio resultante da multiplicação dos dois fatores são as suas respectivas raízes, ou seja, +2 e -1.
![Rendered by QuickLaTeX.com \displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-416399918b5a2a051a6bfc7343ef7960_l3.png)
Exercícios resolvidos sobre raízes de polinômios
Exercício 1
Determine se
![]()
é uma raiz do seguinte polinômio:
![]()
Para descobrir se
![]()
é uma raiz do polinômio, precisamos avaliá-lo com esse valor. Ainda:
![Rendered by QuickLaTeX.com \begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c88c4456693b0c57d55aba68287414c_l3.png)
O valor numérico do polinômio em
![]()
é zero, então é efetivamente uma raiz do polinômio.
Exercício 2
Calcule todas as raízes do seguinte polinômio:
![]()
Primeiro, para encontrar as possíveis raízes do polinômio, devemos encontrar os divisores do termo independente. Então, os divisores de 2 são:
Divisores de 2: +1, -1, +2, -2
As possíveis raízes ou zeros do polinômio são, portanto, ±1 e ±2. Portanto, precisamos calcular quanto o polinômio está em todos esses valores:
![]()
![]()
![]()
![]()
Assim, o polinômio desaparece quando x é +1 ou +2, então aqui estão as raízes do polinômio:
Raízes ou zeros do polinômio : +1 e +2
Exercício 3
Encontre as raízes do seguinte polinômio:
![]()
Devemos primeiro encontrar os divisores do termo independente, pois a raiz de um polinômio também é um divisor do termo independente. Então, os divisores de 4 são:
Divisores de 4: +1, -1, +2, -2, +4, -4
As possíveis raízes ou zeros do polinômio são, portanto, ±1, ±2 e ±4. Devemos, portanto, encontrar o valor numérico do polinômio em todos estes valores:
![]()
![]()
![]()
![]()
![]()
![]()
Assim, o polinômio só desaparece quando x é +1, +2 ou -2, então aqui estão as raízes do polinômio:
Raízes ou zeros do polinômio : +1, +2 e -2
Exercício 4
Encontre as raízes do seguinte polinômio:
![]()
Neste caso, o polinômio não possui termo independente. Portanto, de acordo com a quarta propriedade das raízes explicada acima, sabemos que uma das raízes do polinômio deve ser 0.
Raízes do polinômio:
![]()
Além disso, neste caso, as raízes possíveis não são os divisores do termo independente, mas sim as do coeficiente do termo de menor grau, ou seja, 8:
Divisores de 8: +1, -1, +2, -2, +4, -4, +8, -8
Portanto, as possíveis raízes ou zeros do polinômio são ±1, ±2, ±4 e ±8. Devemos, portanto, calcular o valor numérico do polinômio em todos estes valores:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Então o polinômio desaparece quando x é +2 ou +4, então esses valores são as raízes do polinômio. No entanto, também precisamos de adicionar a raiz 0 que encontrámos no início do problema. Concluindo, todas as raízes do polinômio são:
Raízes ou zeros do polinômio : 0, +2 e +4
Exercício 5
Use as propriedades das raízes dos polinômios para calcular as raízes do seguinte polinômio:
![]()
Como vimos na sexta propriedade das raízes, quando o polinômio é formado pelo produto dos fatores, não é necessário calcular todas as raízes, pois as raízes do polinômio inteiro são as raízes de cada fator.
Além disso, da segunda propriedade das raízes dos polinômios, podemos deduzir que a raiz do primeiro fator é +1 e a raiz do segundo fator é -3.
![]()
![]()
Então, só precisamos de determinar as raízes do último fator. Para fazer isso, encontramos os divisores do termo independente (-2):
Divisores de -2: +1, -1, +2, -2
Portanto, as possíveis raízes ou zeros do último polinômio são ±1 e ±2. Com o qual devemos calcular o valor numérico do referido polinômio em todos estes valores:
![]()
![]()
![]()
![]()
![]()
As raízes do polinômio à direita são, portanto, -1 e 2.
Portanto, as raízes de todo o polinômio são todas as raízes encontradas:
Raízes ou zeros do polinômio : +1, -1, +2, -3