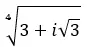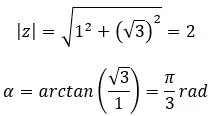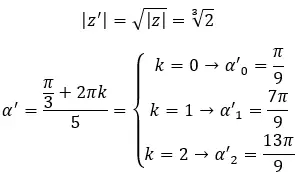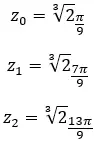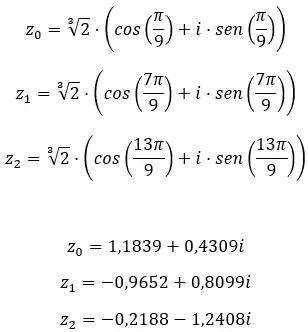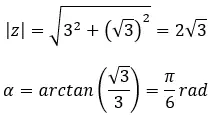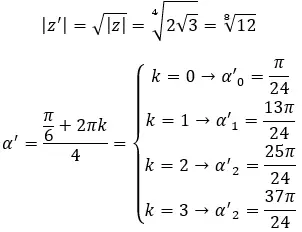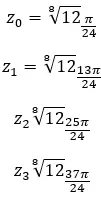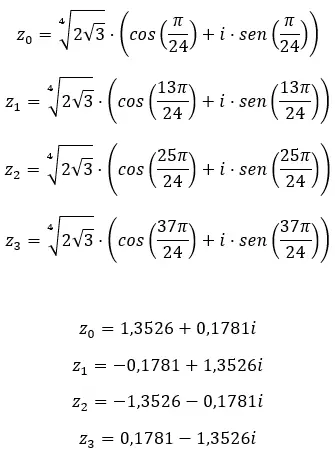Calcular as raízes de números complexos é bastante simples. Bem, depois de entender o procedimento, ele se torna bastante repetitivo. A seguir explicaremos e daremos um exemplo, para que você aprenda como aplicá-lo em exercícios reais.
enésimas raízes de números complexos
O conceito de raiz enésima equivale a dizer raiz de ordem n, portanto, o mesmo método é usado para calcular a raiz quadrada e a raiz quinta de um número complexo. É claro que o número de soluções mudará dependendo desta ordem.
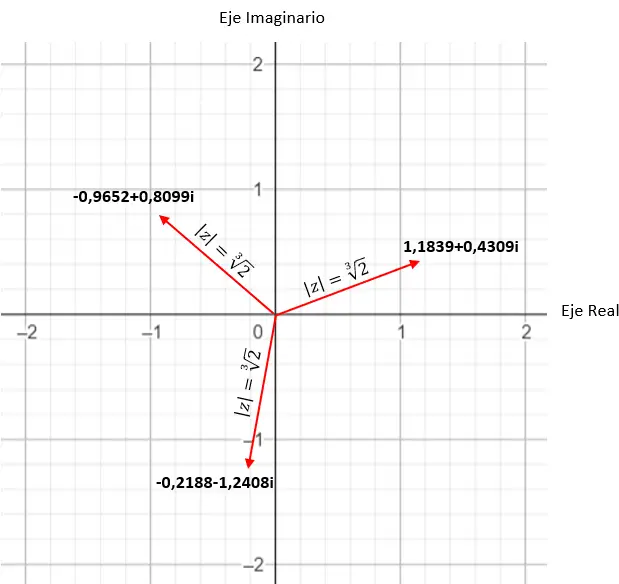
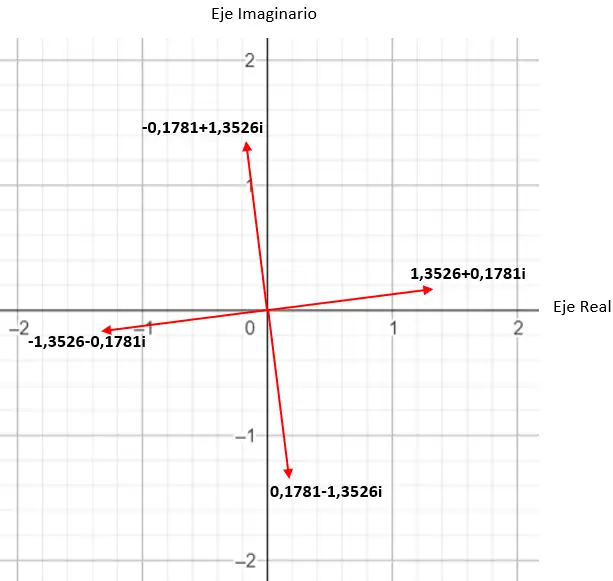
Por exemplo, se calcularmos a raiz quarta de um complexo, obteremos 4 soluções diferentes. E se expressarmos no plano complexo , vemos que se forma um polígono regular de 4 lados, centrado na origem do plano. Esta é uma propriedade muito interessante, que veremos em detalhes mais adiante (na seção de exemplos).
Agora que esclarecemos esse conceito, veremos como calcular a raiz de um número complexo na forma polar (usar esta notação é a mais confortável para resolver uma raiz). Simplesmente, você precisa calcular a raiz do módulo e expressar o argumento em termos de n. Em outras palavras, a raiz do seguinte número complexo (z):
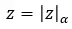
Esses valores para calcular:
- Módulo: A enésima raiz do módulo inicial.
- Argumento: Adicione 2πk em radianos ou 360k em graus ao argumento e divida por n.
Matematicamente, para calcular o módulo e o argumento usamos as duas fórmulas a seguir:
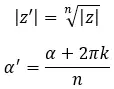
Onde, k = 0, 1, 2,…, n-1.
E, portanto, expressamos o resultado da seguinte forma:
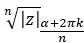
Para ficar claro, as n soluções que obteremos resolvendo esta raiz serão formadas pelo mesmo módulo e n argumentos diferentes.
Exemplos de cálculo de enésimas raízes de complexos
Veremos agora alguns exemplos de cálculo das raízes enésimas de números complexos. Recomendamos que você tente resolvê-los sozinho e, quando terminar, verifique a correção. Não esqueça que o método é explicado logo acima.
Encontre a terceira raiz do número complexo: 1 + i √3 .
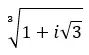
Encontre a quarta raiz do número complexo: 3+i √ 3 .