Matriz regular ou invertível

Nesta página você encontrará a explicação de uma matriz regular ou invertível e como saber quando a inversão de uma matriz pode ser realizada e quando não. Além disso, você também verá vários exemplos de matrizes regulares para entender completamente o conceito e, por fim, mostraremos todas as propriedades desse tipo de matriz.

O que é uma matriz regular?

A definição de uma matriz regular é a seguinte:

Uma matriz regular é uma matriz quadrada que pode ser invertida, ou seja, o inverso dessa matriz pode ser calculado. Portanto, seu determinante é diferente de zero (0).

Matrizes regulares também são chamadas de matrizes invertíveis, não singulares ou não degeneradas .

A matriz oposta à matriz regular é a matriz singular ou degenerada.

Assim, para saber quando uma matriz é regular ou singular, ou seja, quando uma matriz é invertível ou não, basta resolver o determinante da matriz:

Se o determinante da matriz for diferente de zero, a matriz é regular ou invertível.

Se o determinante da matriz for igual a zero, a matriz é singular ou não invertível.

Concluindo, calcular o determinante de uma matriz é a maneira mais simples de saber se a matriz tem inversa ou não, então é isso que recomendamos para determinar a invertibilidade de qualquer matriz.

Se você quiser saber como inverter uma matriz, você pode conferir a fórmula da matriz inversa , que explica passo a passo como inverter uma matriz, e você também encontrará diversos exemplos e exercícios resolvidos para praticar.

Exemplos de matrizes regulares ou invertíveis

Depois de vermos o significado de matriz regular ou invertível, vejamos alguns exemplos de matrizes regulares de diferentes dimensões:

Exemplo de matriz 2×2 regular ou invertível

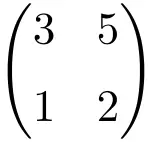
Podemos verificar que é uma matriz regular calculando seu determinante:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

O determinante da matriz de ordem 2 é diferente de 0, portanto é uma matriz regular.

Exemplo de matriz 3×3 regular ou invertível

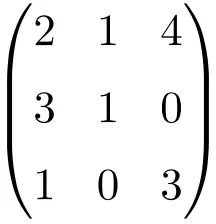
exemplo de matriz regular ou invertível de dimensão 3x3

Devemos fazer o determinante da matriz para verificar que é uma matriz invertível:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

O determinante da matriz de ordem 3 dá um resultado diferente de 0, portanto é uma matriz regular.

Exemplo de matriz 4×4 regular ou invertível

exemplo de matriz regular ou invertível de dimensão 4x4

Tomar o determinante da matriz mostra que ela é uma matriz regular:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

O determinante da matriz de ordem 4 não é zero, é portanto uma matriz invertível.

Atenção: Se tiver dúvidas sobre os cálculos de determinantes, pode consultar a página como calcular um determinante .

Propriedades de matrizes regulares ou invertíveis

Matrizes regulares ou invertíveis são muito importantes para a álgebra linear, e isso se deve às seguintes características:

Se A é uma matriz invertível, sua matriz transposta ou transposta também o é. Além disso, a matriz inversa da transposta é igual à transposta da inversa.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

O contradomínio de uma matriz regular é sempre o máximo possível, ou seja, o contradomínio equivale à dimensão da matriz.

O produto matricial entre duas matrizes invertíveis dá origem a outra matriz regular. Esta condição pode ser facilmente demonstrada com as propriedades dos determinantes:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Toda matriz ortogonal é ao mesmo tempo uma matriz regular.

Seja A a matriz que representa um sistema de equações lineares
$(Ax=b)$

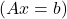
, se A é uma matriz regular, o sistema tem uma solução única, é portanto um sistema determinante compatível (SCD).

Além disso, se o sistema for um sistema homogêneo
$(Ax=0)$

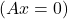
e A pode ser invertido, a solução do sistema é trivial:

$x=0.$

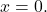
As colunas e linhas de uma matriz regular são linearmente independentes umas das outras.

Todos os autovalores (ou autovalores) de uma matriz regular ou invertível são diferentes de zero.

Matriz invertível de ouro regular