Magic Squares é um jogo matemático que treina nossas habilidades de cálculo de uma forma divertida e emocionante. É por isso que é um dos melhores recursos para ensinar matemática a jovens estudantes.
O que é uma matriz mágica e como ela é resolvida?
Um quadrado mágico é uma espécie de tabela ou matriz composta por diferentes caixas, nas quais são escritos números inteiros . Mas, em hipótese alguma poderão ser instalados; uma série de regras devem ser respeitadas:
- Todas as somas mágicas (somas de todos os valores de qualquer linha horizontal, vertical ou diagonal) devem sempre dar o valor equivalente à constante mágica (é um valor único).
- Nenhum número pode ser repetido duas vezes.
- Você só pode utilizar números consecutivos (por exemplo, de 1 a 9) ou números que sigam uma determinada série, por exemplo: números ímpares, múltiplos de 5, entre outros.
Além disso, é importante ressaltar que podemos fazer diferentes classificações de quadrados dependendo de sua estrutura. A primeira é de acordo com o grau do quadrado , que equivale ao número de células que estão em uma linha ou coluna. E a segunda é de acordo com o tipo de grau da tabela ( números pares ou ímpares). A partir dessas distinções podemos organizar todos os quadrados em diferentes categorias, embora detalharemos isso mais tarde.
Como resolver quadrados mágicos?
Para resolver este jogo matemático, podemos usar dois métodos diferentes: usar a geometria ou calcular a constante mágica. Ambos os procedimentos são igualmente válidos, embora um permita alcançar o resultado mais rapidamente, enquanto o outro exija mais tempo e raciocínio . A seguir explicaremos os dois métodos, para que você escolha o que preferir e se adapte melhor a cada situação.
Qual é a fórmula dos quadrados mágicos?
O primeiro método consiste em calcular a constante mágica , para a qual devemos utilizar a seguinte fórmula: n(n 2 +1)/2, onde n é o grau do quadrado. E uma vez obtido este valor, resta apenas experimentar as diferentes combinações de números, que nos permitem igualar as somas mágicas de todo o quadrado à constante. Em outras palavras, precisamos formar combinações de números que somem o valor da constante, para que todo o quadro fique equilibrado.
Como resolver quadrados mágicos usando geometria?
Segundo, podemos resolver quadrados mágicos usando geometria . Embora deva ser destacado que este método é muito simples e não requer o exercício de suas habilidades de cálculo, pois é puramente metódico. Dito isto, explicaremos o procedimento para resolver quadrados de ordem par e quadrados de ordem ímpar.
Como resolver quadrados mágicos com números ímpares?
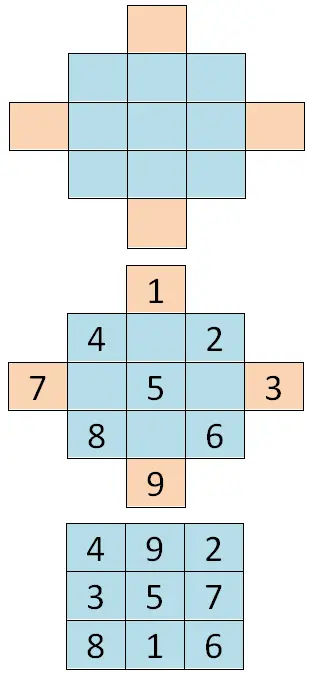
Para resolver este primeiro caso, deve-se adicionar células à tabela inicial de forma que fique uma espécie de losango. Depois temos que escrever todos os números consecutivos começando pelo primeiro dígito da série (no nosso caso 1) e seguiremos as diagonais do losango . Por fim, precisamos “dobrar” o valor, pois os valores das células externas vão para o lado oposto. Então as células externas do eixo vertical se cruzam, então o mesmo acontece com as células do eixo horizontal, abaixo você pode ver um exemplo:
Como resolver quadrados mágicos de ordem par?
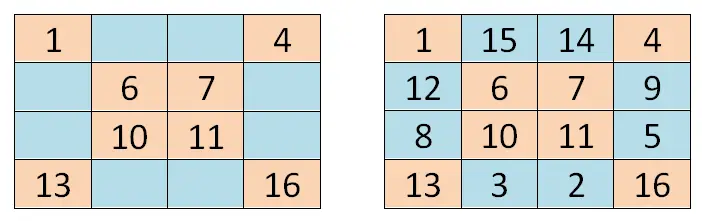
Para resolver um quadrado mágico de ordem par (quadrados mágicos que possuem um número par de linhas e colunas), podemos recorrer a um método um pouco diferente do anterior, mas que também se baseia na geometria. Começaremos escrevendo o primeiro número da série (no nosso caso 1) no canto superior esquerdo. A seguir percorreremos as duas diagonais principais e escreveremos os valores correspondentes à posição de cada caixa.
Depois de escrevermos as duas diagonais principais, teremos que nos colocar na primeira caixa vazia começando no canto inferior direito (caixa 15 no nosso caso). Lá escreveremos o segundo valor da série e escreveremos os demais valores em ordem (do menor para o maior), completando as células da direita para a esquerda e de baixo para cima . Para deixar mais claro, você pode se orientar pela imagem que mostramos a seguir:
Como construir quadrados mágicos?
Para construirmos nós mesmos quadrados mágicos podemos seguir vários procedimentos, entre os quais destacaremos dois. Deve-se destacar que cada um será utilizado para criar quadrados de diferentes tipos, portanto você terá que escolher o método com cuidado dependendo do quadrado que deseja gerar:
Método siamês
Este primeiro método é bastante simples e nos ajuda especificamente a construir quadrados mágicos estranhos de qualquer tamanho. O procedimento a seguir é muito simples, basicamente escreveremos o primeiro número da série na caixa central da primeira linha. A partir daí voltaremos na progressão aritmética que escolhemos, escrevendo o próximo número para cima e para a direita . Porém, se esta posição estiver fora do quadrado desenhado, teremos que passar para a última linha ou coluna. E se terminarmos com um quadrado completo, teremos que descer um quadrado a partir do último quadrado numérico que inserimos e então continuaremos da mesma maneira.
Abaixo você pode ver um exemplo de 3×3:
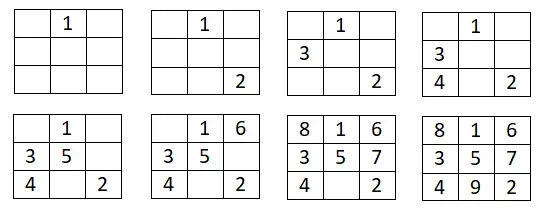
Método de Strachey para quadrados mágicos
Para gerar quadrados mágicos de ordem 4k + 2 pares , utilizaremos este outro método, que se baseia no anterior (método siamês) e que também é muito simples. Abaixo você pode ver os passos a seguir e um exemplo prático de um quadrado mágico 6×6:
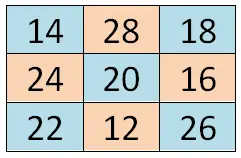
- Dividir em quadrantes menores: A primeira coisa que precisamos fazer é subdividir o tabuleiro em quadrados menores, por exemplo se tivermos um tabuleiro 6×6 precisaremos fazer quatro quadrantes iguais de quadrados 3×3.
- Use o método siamês: então atribuiremos um intervalo de números a cada pequeno quadrante, por exemplo, se iniciarmos a sequência com 1, os intervalos seriam: 1-9 (primeiro), 10-18 (quarto), 19-27 (segundo) e 28-36 (terceiro).
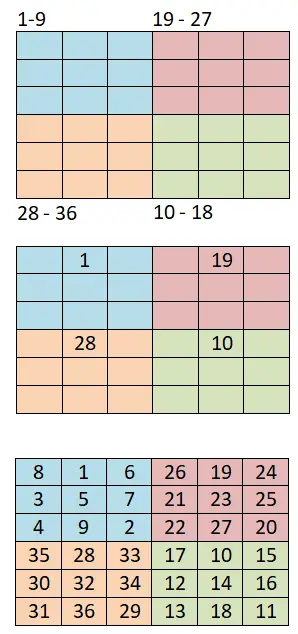
Método LUX de Conway para quadrados mágicos
Usaremos o último sistema quando quisermos gerar quadrados mágicos de ordem 4n + 2 , onde n é um número natural. Assim, o procedimento que seguiremos para criar quadrados deste estilo é o seguinte:
- Criando a tabela ou matriz: começaremos criando uma matriz de grau 2n + 1, onde n é um número natural. Com isso poderemos desenhar a mesa e teremos em mente o seu grau e então começaremos com o desenho.
- Posicionamento das letras: uma vez construída a tabela, você terá que escrever de cima para baixo: n + 1 linhas de L, 1 linha de U en – 1 linhas de X. E então, você terá que trocar o U no meio com o L no topo.
- Troque letras por valores numéricos: Agora precisaremos substituir as letras por grupos de quatro números consecutivos. Dependendo da letra, daremos uma ordem ou outra aos números. Explicado abaixo:
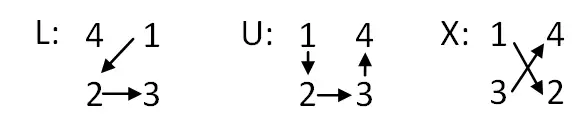
Começaremos construindo uma matriz 5×5 , então n = 2, pois: 2n + 1 = 2 · 2 + 1 = 5. Isso significa que a matriz acabará tendo um tamanho de 10×10, pois como As como já dissemos, cada célula que contém uma letra equivale a um grupo de quatro números, ou seja, uma matriz 2×2. Abaixo você confere o exemplo finalizado, no qual substituímos cada letra por um grupo de quatro números na ordem mostrada na imagem:
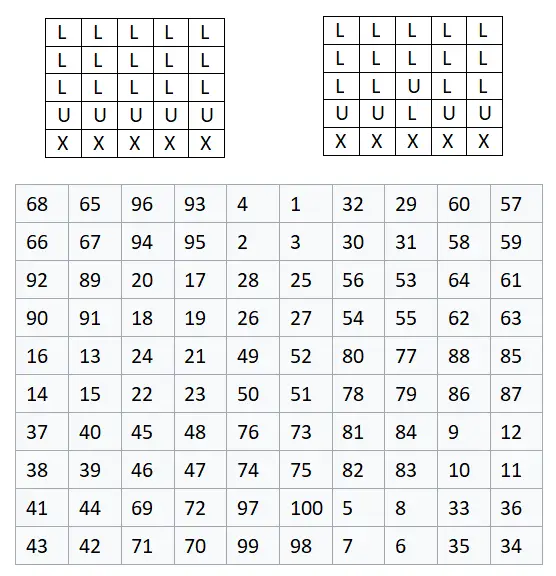
exercícios de quadrados mágicos
A seguir, oferecemos alguns quadrados mágicos incompletos e você mesmo deverá preenchê-los, graças aos conceitos que explicamos neste artigo. Lembre-se de que você pode usar qualquer um dos métodos ensinados. Além disso, é preciso levar em consideração que 1 pode não ser o primeiro número da série, embora o coloque na declaração. E ao terminar um dos exercícios, você poderá ver a solução abaixo do enunciado.
quadrado mágico 3×3
Construa um quadrado mágico 3×3 apenas com números ímpares:
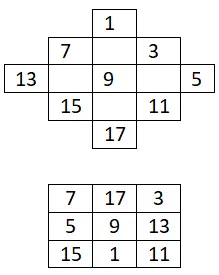
Quadrado mágico 4×4
Complete o seguinte quadrado mágico 4×4:
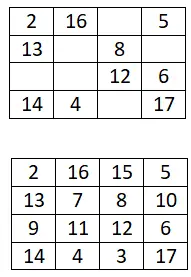
quadrado mágico 5×5
Complete o seguinte quadrado mágico 5×5:
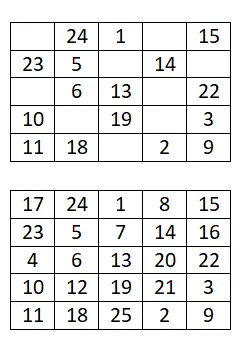
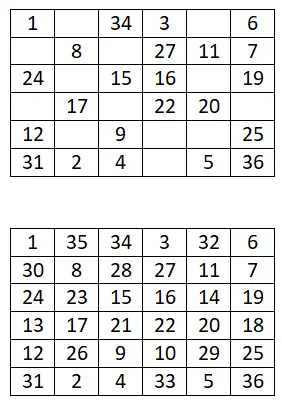
quadrado mágico 6×6
Complete o seguinte quadrado mágico 6×6: