Número combinatório (ou coeficiente binomial)

Nesta página explicamos o que é um número combinatório e como é calculado (fórmula). Além disso, você poderá ver exemplos de como calcular qualquer número combinatório e praticar com exercícios resolvidos passo a passo. Também mostramos todas as propriedades e aplicações dos números combinatórios. E por fim, aprendemos como encontrar o resultado de um número combinatório diretamente com a calculadora.

O que é um número combinatório?

Em matemática, o número combinatório , também chamado de coeficiente binomial, é o número de combinações ordinárias (combinações sem repetição) de grupos de k elementos que podem ser formados a partir de um conjunto de n elementos (n>k).

Um número combinatório é expresso entre parênteses da seguinte forma:

\begin{pmatrix}n \\ k \end{pmatrix}

Por outro lado, o número combinatório é lido n sobre k . Da mesma forma, n é chamado de numerador e k é chamado de ordem.

Apenas com a definição de número combinatório fica difícil entender seu significado. Porém, veremos agora como o número combinatório é determinado matematicamente, e depois nos aprofundaremos neste conceito de combinatória. Você verá que assim entenderá melhor.

Fórmula numérica combinatória

A fórmula para calcular o valor de um número combinatório (ou coeficiente binomial) é a seguinte:

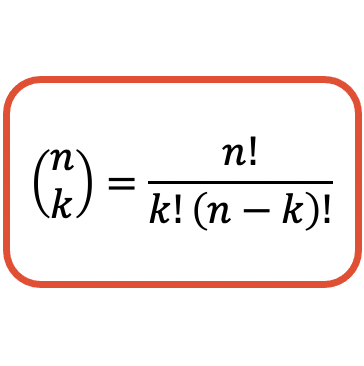
fórmula numérica combinatória

Lembre-se que em álgebra o ponto de exclamação corresponde ao fatorial de um número. E para encontrar o fatorial de um número, você precisa multiplicar todos os números inteiros positivos de 1 por esse número. Por exemplo, para calcular o fatorial do número 4 você deve multiplicar 1, 2, 3 e 4:

4! = 1\cdot 2 \cdot 3 \cdot 4 =24

Também é importante saber que o fatorial de 0 é igual a 1.

0! = 1

Exemplo de cálculo de um número combinatório

A seguir, determinaremos passo a passo o valor de um número combinatório como exemplo, para que você possa ver como isso é feito:

  • Calcule o valor do número combinatório 5 sobre 3.

O coeficiente binomial de 5 sobre 3 corresponde à seguinte expressão:

\begin{pmatrix}5 \\ 3 \end{pmatrix}

Portanto, se aplicarmos a fórmula para números combinatórios, para determinar seu valor devemos realizar as seguintes operações:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}

Ou equivalente:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}

Portanto, encontramos os fatoriais:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}

A multiplicação 1·2·3 é repetida no numerador e no denominador, então a fração pode ser simplificada eliminando este fator:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}

Agora calculamos os produtos:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}

E por fim, fazemos a divisão:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}

Propriedades do número combinatório

Números combinatórios, ou coeficientes binomiais, podem ser combinados de acordo com as seguintes propriedades:

  • Dois números combinatórios complementares são aqueles que possuem o mesmo numerador n e a soma de suas ordens é equivalente ao referido numerador. Assim, o resultado de dois números combinatórios complementares é idêntico.

\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}

Essa característica dos números combinatórios também é chamada de identidade de simetria.

Por exemplo, 6 sobre 4 dá o mesmo resultado que 6 sobre 2, porque 6-4=2.

\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}

\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}

  • A soma de dois números combinatórios com o mesmo numerador e ordens sucessivas é igual a outro número combinatório cujo numerador equivale ao numerador das adições mais 1 e cuja ordem corresponde ao maior valor das ordens das adições. Em outras palavras, a seguinte condição é sempre atendida:

\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}

Por exemplo:

\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}

Esta propriedade também é conhecida como regra de Pascal.

Por outro lado, esta fórmula também pode ser aplicada ao contrário para decompor um número combinatório em dois números combinatórios mais simples:

\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}

Por exemplo, o número combinatório 8 sobre 4 é igual a 7 sobre 3 mais 7 sobre 4:

\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}

  • Qualquer número positivo maior que 1 é igual ao próprio número.

\begin{pmatrix}n\\ 1 \end{pmatrix} =n

A razão para esta propriedade é que o fatorial de um número é igual ao fatorial do número anterior multiplicado pelo próprio número:

\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n

Exemplos deste tipo de números combinatórios:

\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9

  • Qualquer número positivo maior que 0 é igual a um.

\begin{pmatrix}n\\ 0 \end{pmatrix} =1

Na verdade, o denominador da fração de tal número combinatório será sempre igual ao numerador da fração:

\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1

Exemplos de números combinatórios como este:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1

  • Cada número em si é igual a 1.

\begin{pmatrix}n\\ n \end{pmatrix} =1

Aqui está a demonstração:

\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1

Exemplos de números combinatórios como este:

\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1

Como calcular um número combinatório com a calculadora

Até agora vimos como encontrar um número combinatório de números mais ou menos simples, mas quando temos que operar com quantidades muito grandes é melhor usar a calculadora para determinar o número combinatório. Veremos agora como inserir um número combinatório na calculadora.

Assim, a chave usada para calcular um número combinatório com a calculadora é a chave nCr . E para determinar o valor do número combinatório, você deve primeiro inserir o numerador do número combinatório, em segundo lugar pressionar a tecla nCr, depois inserir a ordem do número combinatório e por fim pressionar a tecla igual.

\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}

Nas calculadoras científicas CASIO, a tecla nCr geralmente possui um botão próprio ou fica acima do botão de divisão, dependendo do modelo.

Por exemplo, se quisermos saber qual é o número combinatório 10 sobre 6, devemos fazer a seguinte sequência:

\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210

Aplicações do número combinatório

Se você chegou até aqui, provavelmente já sabe como resolver qualquer número combinatório, perfeito. Mas… para que serve o número combinatório? Pois bem, veremos então todas as vantagens que este tipo de operação tão especial apresenta.

Combinatória

Como vimos no topo da página, o resultado de um número combinatório

\begin{pmatrix}n\\ k \end{pmatrix}

representa o número de grupos possíveis de

k

elementos que podem ser formados a partir de um conjunto de um total de

n

Unid.

Portanto, alguns problemas combinatórios podem ser resolvidos usando números combinatórios (ou coeficientes binomiais). Vamos ver como fazer isso usando um exemplo:

  • Numa turma de 30 alunos, queremos escolher um grupo de 4 alunos para realizar determinadas tarefas. Qual é o número total de grupos diferentes que podem ser formados?

Neste caso, a ordem dos alunos não importa, o mesmo aluno não se repete duas vezes dentro do grupo e nem todos os alunos entram no grupo. Portanto, a fórmula numérica combinatória pode ser usada para determinar de quantas maneiras o grupo pode ser formado.

Para isso, deve-se calcular o número combinatório tendo o número total de alunos como numerador e com o número de alunos que formarão o grupo como ordem:

\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}

O número total de combinações possíveis é, portanto, de 27.405 grupos.

Binômio de Newton

Outra aplicação dos números combinatórios é o binômio de Newton. O binômio de Newton é um polinômio composto por dois termos elevados juntos a um número inteiro, ou seja, o binômio de Newton é aquele polinômio que responde à seguinte expressão algébrica:

(a+b)^n

Obviamente, se o binômio for elevado ao quadrado, isso significa que é uma identidade notável e, portanto, pode ser facilmente calculada com a fórmula correspondente. Por outro lado, quando o binômio é elevado a números grandes, o cálculo torna-se bastante difícil. Bem, o teorema binomial de Newton diz que esses tipos de polinômios podem ser calculados muito facilmente a partir de números combinatórios.

Clique no link a seguir e descubra o que é a fórmula binomial de Newton e como ela é calculada. Além disso, você poderá ver exemplos e praticar com exercícios resolvidos passo a passo. E finalmente, você descobrirá a curiosa história deste teorema.

Triângulo de Tartaglia (ou Pascal)

Como você viu ao longo deste artigo, calcular manualmente o coeficiente binomial de números grandes pode ser trabalhoso e complicado.

Por outro lado, com o triângulo de Tartaglia, também chamado de triângulo de Pascal, todos os números combinatórios podem ser facilmente determinados usando uma regra mnemônica. Isto é logicamente muito útil, pois economiza muito tempo durante os cálculos.

Para descobrir exatamente como fazer isso, veja a explicação do triângulo de Tartaglia . Nesta página vinculada você descobrirá o que é esse misterioso triângulo, para que serve (tem aplicações surpreendentes) 😮 e qual a sua origem (já era usado há mais de 1000 anos).

Exercícios de números combinatórios resolvidos

Para que você possa praticar e compreender totalmente os conceitos explicados, deixamos vários exercícios resolvidos passo a passo sobre números combinatórios.

Exercício 1

Encontre o número combinatório 9 por 5 (sem usar calculadora).

Para encontrar o valor do número combinatório 9 de 5 simplesmente aplicamos a fórmula fatorial:

\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}

Exercício 2

Qual é o resultado da seguinte soma de dois números combinatórios? (sem calculadora)

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}

Das propriedades dos números combinatórios, segue-se que a soma do problema é igual ao seguinte número combinatório:

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}

Portanto, basta calcular o número combinatório 11 de 7:

\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}

Exercício 3

Determine se os seguintes números combinatórios são iguais:

\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}

Para encontrar o resultado dos três números combinatórios, não é necessário usar uma calculadora, mas eles podem ser facilmente encontrados graças às propriedades dos números combinatórios.

Em primeiro lugar, um número combinatório de qualquer número maior que 0 dá 1. Portanto:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1

Por outro lado, qualquer número maior que um é igual ao próprio número. Ainda:

\begin{pmatrix}6\\ 1 \end{pmatrix} =6

E por fim, qualquer número combinatório formado pelo mesmo número repetido duas vezes equivale a 1. Portanto:

\begin{pmatrix}6\\ 6 \end{pmatrix} =1

Concluindo, o primeiro e o terceiro números combinatórios do problema são iguais, porém são diferentes do número combinatório intermediário.

\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima