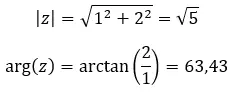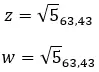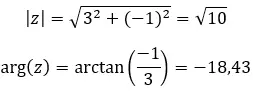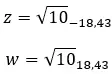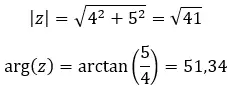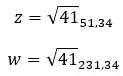Neste artigo discutiremos as propriedades dos números complexos , que podem ser úteis na resolução de cálculos e na simplificação de expressões. Vamos direto a essas propriedades.
Módulo e argumento de um número complexo
A primeira propriedade de um número complexo é o módulo e o argumento de um número complexo. É muito fácil de calcular, pois basta aplicar algumas fórmulas.
A fórmula para calcular o módulo:

A fórmula para calcular o argumento:

Agora, se o número for expresso na forma polar ou trigonométrica, não há necessidade de fazer nenhum cálculo. Porque, na mesma expressão, módulo e argumento estão listados.
Na imagem abaixo você pode ver a fórmula para um número na forma polar, onde |z| é o módulo e α é o argumento.

E nesta outra imagem você pode ver a estrutura de um número expresso na forma trigonométrica, onde |z| é o módulo e α é o argumento.

números complexos iguais
Números complexos iguais são aqueles que compartilham módulo e argumento. Então, desses dois valores:

Eles são iguais se a seguinte propriedade for atendida.
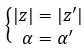
Por outro lado, se tivermos ambos os números na forma binomial, podemos fazer uma verificação muito rápida e fácil para ver se são dois números complexos iguais. Simplesmente, a seguinte expressão deve ser cumprida:
a + bi = a + bi
Vejamos um exemplo, determine se os dois números complexos a seguir são iguais:
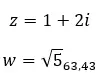
Conjugar números complexos
Agora vamos passar para uma das propriedades mais importantes dos números complexos, pois saber calcular o conjugado de um complexo nos ajuda muito na resolução de divisões complexas e na realização de simplificações.
Então, desses dois valores:

Dizemos que são conjugados se compartilham um módulo e possuem argumentos opostos. Deve, portanto, ser preenchido:
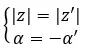
Por outro lado, se tivermos ambos os números na forma binomial, podemos fazer uma verificação muito rápida e fácil para ver se são dois números complexos conjugados. Simplesmente, a seguinte expressão deve ser cumprida:
um + bi = um – bi
Vejamos um exemplo, determine se os dois números complexos a seguir são conjugados:
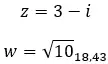
Números complexos opostos
A seguir, passamos a ver a propriedade dos números complexos opostos. Destes dois valores:

Podemos dizer que são opostos se tiverem o mesmo módulo e seus argumentos diferirem em 180 graus ou π radianos:
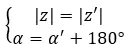
Por outro lado, se tivermos ambos os números na forma binomial, podemos utilizar outro método ainda mais rápido e simples para descobrir se são dois números complexos opostos. Simplesmente, a seguinte expressão deve ser cumprida:
uma + bi = -a – bi
Vejamos um exemplo, determine se os dois números complexos a seguir são opostos:
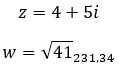
outras propriedades
Obviamente, esse conjunto de números possui outras propriedades, como números complexos inversos e algumas outras que estão diretamente relacionadas às operações aritméticas básicas. Embora tudo isso seja abordado em outros artigos, que você pode ver na lista abaixo.