Propriedades dos determinantes

Nesta seção, veremos quais são todas as propriedades dos determinantes . Também demonstramos cada propriedade com um exemplo para que você as entenda completamente. E, além disso, você encontrará exercícios relacionados às propriedades dos determinantes.

A seguir explicaremos cada propriedade dos determinantes uma por uma, mas se preferir pode pular diretamente para a tabela resumo abaixo. 😉

Propriedade 1: Determinante da matriz transposta

O determinante de uma matriz é equivalente ao determinante de sua matriz transposta.

\lvert A \rvert = \lvert A^t \rvert

Exemplo:

\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}

Agora transpomos a matriz 2×2 e resolvemos o determinante. Observe que obtemos o mesmo resultado de antes:

\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}

Propriedade 2: Determinante com linha ou coluna preenchida com zeros

Se um determinante tiver uma linha ou coluna preenchida com zeros, o determinante retornará 0.

\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0

Exemplo:

\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}

Em ambos os exemplos, os determinantes são avaliados como 0. Porque a segunda linha do primeiro determinante é toda zero e a terceira coluna do segundo determinante também é toda zero.

Propriedade 3: Determinante com duas linhas ou colunas iguais

Se um determinante tiver duas linhas iguais ou múltiplas ou duas colunas, o determinante será zero (0).

Portanto, se existe uma combinação linear entre linhas ou colunas, ou seja, são linearmente dependentes, o determinante dá 0.

Exemplo:

\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0

Neste caso, o determinante dá 0 porque as colunas 2 e 3 são iguais.

Propriedade 4: Modifique as linhas ou colunas de um determinante

Se duas linhas ou duas colunas forem modificadas uma em relação à outra, o determinante dá o mesmo resultado, mas com um sinal diferente.

\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}

Exemplo:

\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}

Agora alteramos a ordem das colunas 2 e 3 uma em relação à outra. Observe que o resultado é o mesmo, mas com um sinal diferente:

\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}

Propriedade 5: Multiplique uma linha de um determinante por um escalar

Multiplicar todos os elementos de uma linha ou coluna inteira por um número real é o mesmo que multiplicar o resultado do determinante por esse número.

\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

Exemplo:

\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}

Agora pegamos o mesmo determinante e multiplicamos uma linha inteira por 2. Você verá que o resultado será o do determinante anterior, mas multiplicado por 2, ou 10:

\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}

Propriedade 6: Determinante do produto da matriz

O determinante do produto de duas matrizes é igual ao produto do determinante de cada matriz separadamente.

\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert

Exemplo:

Para demonstrar esta propriedade dos determinantes, calcularemos o determinante da multiplicação das duas matrizes a seguir de duas maneiras possíveis:

\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}

Primeiro multiplicaremos as duas matrizes e depois calcularemos o determinante da matriz resultante:

\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}

Agora calculamos o determinante de cada matriz separadamente e depois multiplicamos os resultados:

\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}

Como você pode ver, fazer primeiro o produto da matriz e depois o determinante dá o mesmo resultado que fazer primeiro o determinante de cada matriz e depois multiplicar os resultados.

Por outro lado, esta condição não se aplica às operações de adição e subtração, ou seja, o determinante da adição (ou subtração) de duas matrizes não dá o mesmo resultado que a adição (ou subtração) dos determinantes de duas matrizes separadamente.

Propriedade 7: Determinante da matriz inversa

Se uma matriz for invertível, o determinante da sua inversa corresponde ao inverso do determinante da matriz original.

\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}

Exemplo:

Verificaremos esta propriedade calculando primeiro a inversa de uma matriz e depois resolvendo o seu determinante. Veremos que o resultado equivale a encontrar o determinante da matriz original e invertê-lo.

Portanto, invertemos a seguinte matriz e calculamos seu determinante:

\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}

\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}

\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}

E agora resolvemos o determinante da matriz original e fazemos o seu inverso:

\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2

\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}

Como você pode ver, os resultados de ambas as operações são idênticos. A propriedade está, portanto, comprovada.

Propriedade 8: Substitua a linha de um determinante

A linha de um determinante pode ser substituída adicionando (ou subtraindo) a mesma linha mais (ou menos) outra linha multiplicada por um número.

Exemplo:

Com o exemplo a seguir verificaremos esta propriedade. Primeiro calcularemos um determinante, depois operaremos em uma linha do determinante e recalcularemos seu resultado. Você verá como obtemos o mesmo resultado em ambos os casos.

Então, vamos primeiro calcular um determinante 3×3 com a regra de Sarrus:

\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}

Agora, na linha 2, adicionamos a primeira linha multiplicada por 2:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}

E resolvemos o determinante depois de transformar uma de suas retas:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}

Em ambos os casos o resultado foi -3. Assim, mostra-se que o resultado de um determinante não muda se uma linha for substituída pela soma da mesma linha mais outra linha multiplicada por um número.

Propriedade 9: Determinante de uma matriz triangular

O determinante de uma matriz triangular é o produto dos elementos de sua diagonal principal.

Exemplo:

Resolveremos o determinante da seguinte matriz triangular como exemplo:

\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}

Propriedade 10: Determinante de uma matriz diagonal

O determinante de uma matriz diagonal é igual à multiplicação dos elementos de sua diagonal principal.

Exemplo:

Tomemos como exemplo o determinante da seguinte matriz diagonal:

\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}

Tabela resumo de propriedades dos determinantes

As propriedades dos determinantes explicadas podem ser resumidas na tabela a seguir:

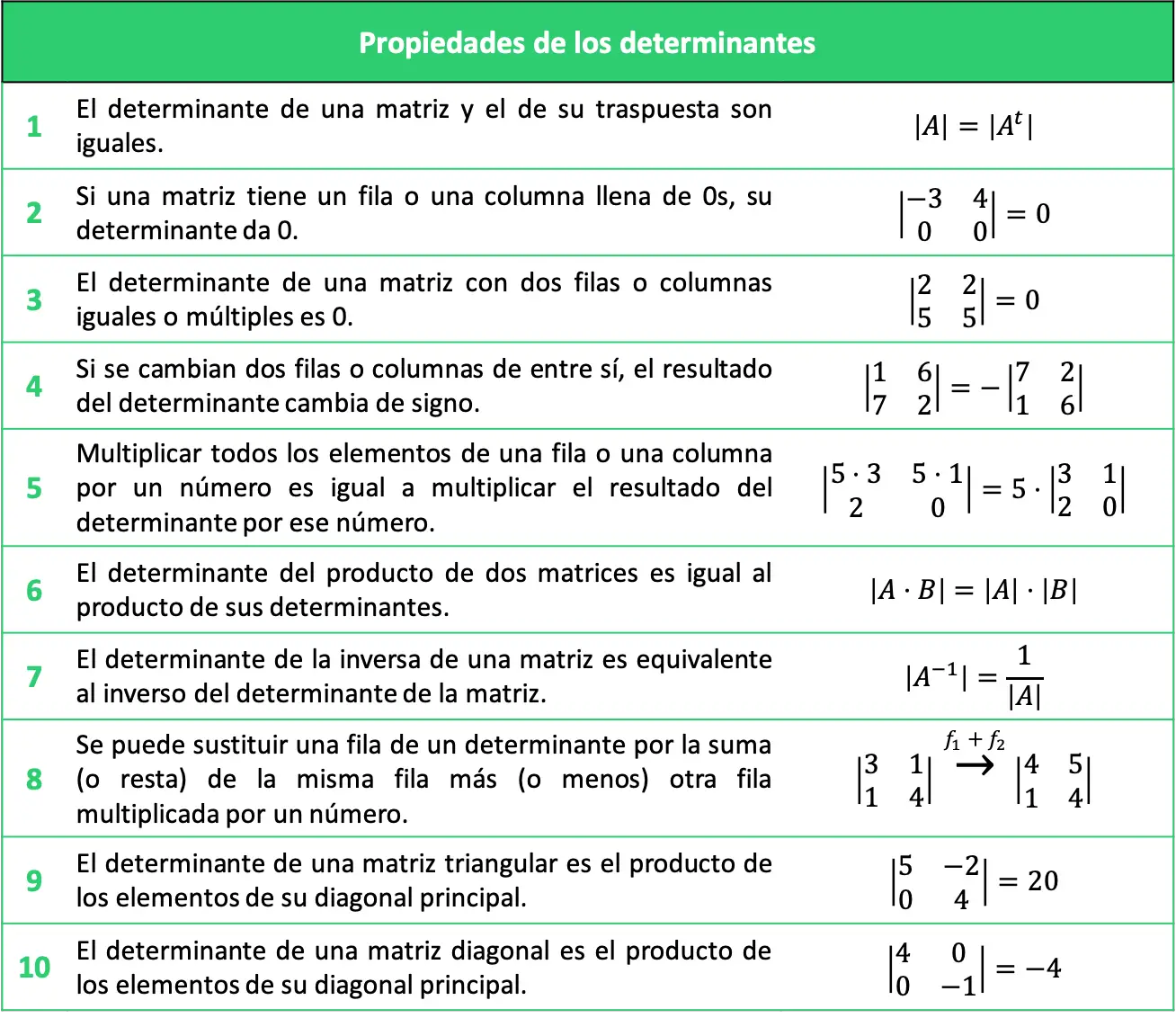
propriedades dos determinantes

Exercícios resolvidos com as propriedades dos determinantes

Exercício 1

Resolva o seguinte determinante:

\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}

Se um determinante tiver uma linha ou coluna preenchida com zeros, o determinante retornará 0 (propriedade 2). Portanto, o resultado do determinante é 0, pois a terceira coluna é preenchida com zeros.

Exercício 2

Resolva o seguinte determinante:

\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}

Se um determinante tiver duas linhas iguais ou múltiplas ou duas colunas, o determinante retornará 0 (propriedade 3). Portanto, o resultado do determinante é 0, porque a primeira linha e a terceira linha são iguais.

Exercício 3

Calcule o seguinte determinante:

\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}

Se um determinante tiver duas linhas iguais ou múltiplas ou duas colunas, o determinante retornará 0 (propriedade 3). Portanto, o resultado do determinante é 0, porque a quarta coluna é o dobro da primeira coluna.

Exercício 4

Conhecemos o resultado de um determinante, embora não conheçamos os elementos da matriz:

\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3

A partir do resultado do determinante anterior e das propriedades dos determinantes, calcule o resultado dos seguintes determinantes:

\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}

Para)

\begin{pmatrix} a & c \\ b & d \end{pmatrix}

é a matriz transposta de

\begin{pmatrix} a & b \\ c & d \end{pmatrix}

. E o determinante de uma matriz é igual ao determinante de sua matriz transposta (propriedade 1). Portanto, o resultado deste determinante também é 3.

\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}

b) Na determinação

\begin{vmatrix} b & a \\ d & c \end{vmatrix}

as colunas 1 e 2 foram modificadas em relação ao determinante da declaração

\begin{vmatrix} a & b \\ c & d \end{vmatrix}

. Portanto, de acordo com a propriedade 4, o resultado é igual ao resultado do determinante da afirmação, mas com um sinal diferente, ou seja, -3.

\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}

c) Na determinação

\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}

toda a segunda coluna do determinante do enunciado foi multiplicada por 3. Portanto, da propriedade 5 podemos deduzir que seu resultado também será o resultado do determinante do enunciado multiplicado por 3, ou seja, 9.

\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}

Exercício 5

Conhecemos o resultado desses dois determinantes:

\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8

\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4

A partir dessas informações, calcule:

\displaystyle \vert A \cdot B \vert

Para calcular o resultado do determinante não é necessário multiplicar matrizes 4×4. Já o determinante do produto de duas matrizes é igual ao produto do determinante de cada matriz separadamente (propriedade 6). Ainda:

\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima