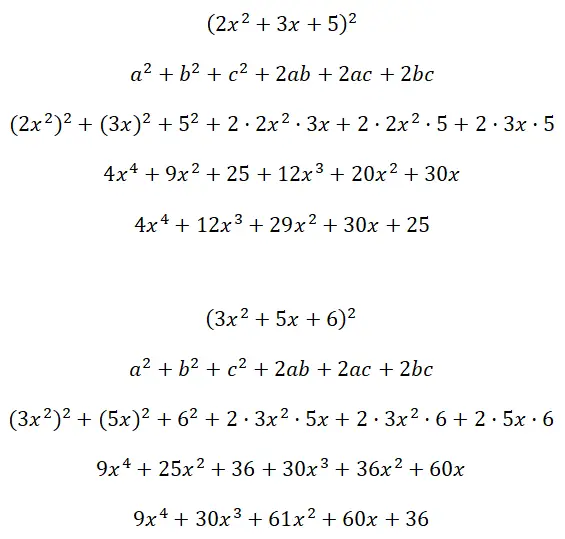Produtos notáveis

O que são produtos notáveis ou identidades notáveis?

Identidades notáveis , também chamadas de produtos notáveis ou igualdades notáveis , são recursos matemáticos que permitem resolver mais rapidamente produtos e quocientes de polinômios . Como indica a palavra identidade, são igualdades que nos permitem calcular estas operações sem ter que resolvê-las. Pois sabemos que esta expressão segue regras fixas (que são sempre cumpridas) e, portanto, podemos obter o resultado sem ter que verificá-lo.

Quando usar uma identidade notável?

Essas identidades são utilizadas principalmente na área de álgebra e têm como principal função agilizar a solução de um determinado polinômio, sem a necessidade de resolver toda a operação em si. A partir daí obtemos as fórmulas de produtos notáveis, que comentaremos ao longo do artigo. E por fim, podemos aplicar as fórmulas para completar quadrados, fatorar polinômios ou qualquer outro tipo de cálculo.

Como resolver passo a passo um produto notável?

Para resolver identidades notáveis, você precisa seguir um procedimento muito simples, que também faz muito sentido:

• Identifique o tipo de identidade notável: O primeiro passo é identificar o tipo de operação: um produto notável ou um quociente notável. Você também deve esclarecer que tipo de fórmula deverá aplicar, embora você entenderá isso mais tarde, depois de explicarmos os diferentes tipos de identidades notáveis.
• Aplique a fórmula: Depois de saber qual fórmula precisa aplicar, é hora de fazer os cálculos. Dependendo do tipo de identidade, terá que resolver operações mais ou menos complexas e na grande maioria dos casos, estes cálculos serão compostos por termos que contêm pelo menos uma incógnita.
• Simplifique a expressão: Finalmente, ao obter o resultado, você precisa simplificá-lo. Nesta etapa, você precisa agrupar termos semelhantes e ordená-los para formar um polinômio resultante bem estruturado. Ressalta-se que esta etapa é tão importante quanto as demais, pois caso contrário o exercício fica incompleto.

Fórmulas de identidades notáveis ou principais produtos notáveis

Abaixo você encontrará todas as fórmulas correspondentes às identidades notáveis. Além da explicação teórica de cada caso, há também alguns exemplos notáveis de produtos resolvidos, através dos quais você entenderá melhor todos os conceitos. Vale ressaltar que nesta primeira seção você encontrará apenas as identidades mais importantes . Mas, ao ler este artigo, você aprenderá como desenvolver produtos notáveis mais complexos, como os feitos de trinômios.

quadrado de uma soma

O primeiro caso diz respeito ao quadrado da soma , que é uma expressão polinomial muito comum no mundo da álgebra. Isso pode ser encontrado escrito como: (a + b) ² , que é equivalente a: (a + b) · (a + b). Portanto, sabemos que pode ser resolvido usando multiplicação polinomial. Mas, graças a identidades notáveis, podemos economizar tempo usando a seguinte fórmula: (a + b) ² = a ² + 2ab + b ² . A seguir mostramos a demonstração da fórmula que acabamos de ver, assim você poderá entender de onde ela vem e como é utilizada:

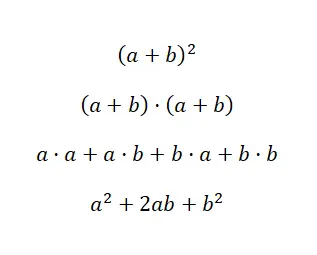
Como podemos ver, realizamos a verificação utilizando a multiplicação de polinômios que comentamos anteriormente. E podemos dizer com absoluta certeza que se você souber de cor a fórmula resultante, então, realizando uma simples substituição de valores , você poderá obter o resultado mais rapidamente. Portanto, é um conceito matemático muito útil. Agora que você sabe como funciona o quadrado de uma soma, mostraremos um exemplo concreto:

Exemplo do quadrado de uma soma

Calcule a identidade notável (2x + 4) ² :

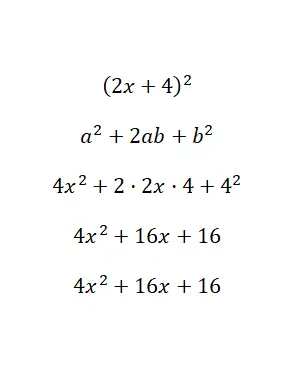
Basicamente associamos os valores do binômio às letras da fórmula e resolvemos: a = 2x e b = 4. Por fim, após resolver todos os cálculos, obtemos o polinômio 4x ² + 16x + 16, que é equivalente ao original . Neste exemplo, obtivemos um polinômio expandido (na forma padrão) a partir de um polinômio reduzido.

quadrado de uma subtração

Outra expressão muito comum é o quadrado da subtração , que é muito parecido com o quadrado da adição, só muda um sinal. Então, a estrutura do binômio equivale a: (a – b) ² , e se a desdobrarmos obtemos: (a – b) · (a – b). Como no caso anterior, este pode ser calculado a partir de uma multiplicação de polinômios, embora também possua uma fórmula que facilita a solução: a ² – 2ab +b ² . Abaixo você encontra a prova empírica disso:

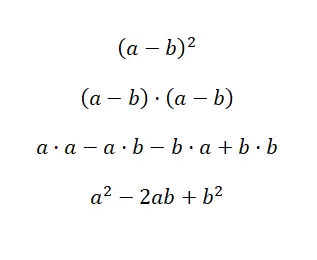
Para simplificar a resolução do quadrado de uma diferença, podemos utilizar a mesma fórmula que utilizámos para a soma de um quadrado, mas com o primeiro sinal negativo . Esta alteração mínima permite que a expressão seja adaptada a binômios compostos por um termo positivo e um termo negativo, o que é útil para subtrações. Mostraremos agora um exemplo resolvido:

Exemplo do quadrado de uma subtração

Calcule a identidade notável (x – 3) ² :

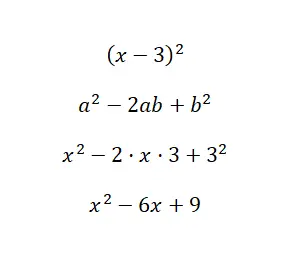
Como você pode ver na solução de exemplo, substituímos os valores do nosso binômio na fórmula, a = x e b = 3. Portanto, usando a fórmula que explicamos anteriormente, só precisamos fazer a substituição e alguns passos muito básicos cálculos. Isto permite-nos ver quão facilmente o quadrado de uma diferença pode ser calculado com esta expressão.

Diferença de quadrados ou soma por diferença

O terceiro caso de produtos notáveis é denominado diferença de quadrados , esta é formada pelo produto de um binômio positivo e um binômio negativo. Uma expressão deste estilo possui a seguinte estrutura: (a + b) · (a – b), portanto se expandirmos este produto obtemos a fórmula que facilita o cálculo: a ² – b ² . Como você pode ver, é uma fórmula muito simples, embora para entendê-la completamente seja necessário desenvolver todos os cálculos:

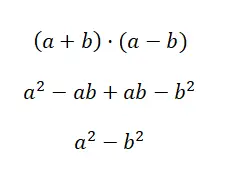
Exemplo de soma por diferença

Calcule a identidade notável (x + 1) · (x – 4):

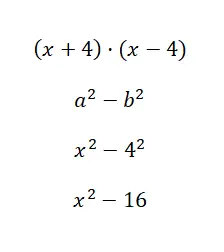
Nesta ocasião, o cálculo numérico é muito fácil, na verdade só tivemos que resolver uma potência. Embora seja verdade que esta fórmula só é aplicável quando os binômios têm o mesmo termo principal e o mesmo termo independente, mas com sinal alterado. Então essa identidade é importante, mas não é a que você mais vai usar.

Produto de dois binômios com um termo comum

Neste quarto caso, encontramo-nos perante uma situação muito semelhante à anterior, embora com uma ligeira modificação na estrutura. Observe a diferença que lhe mostramos: (x + a) · (x + b) e (a + b) · (a – b). Caso você ainda não veja com muita clareza, considere o seguinte exemplo: (x + 4) · (x + 5) e (x + 4) · (x – 4). No primeiro caso (o produto de dois binômios de termos comuns ) há apenas um termo compartilhado, enquanto no segundo caso (a soma por diferença) os dois termos são comuns, mas o termo independente tem seu sinal invertido. Dito isso, vamos ver com qual fórmula podemos agir:

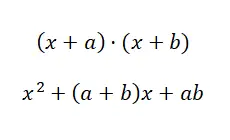
Exemplo do produto de dois binômios com um termo comum

Resolva para o produto notável (x + 2) · (x + 3):

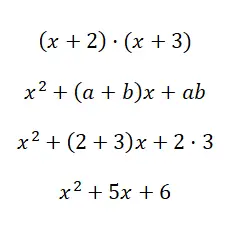
Utilizando a fórmula x ² + (a + b)x + ab podemos calcular o polinômio de segundo grau resultante da multiplicação dos dois binômios. Esperamos que através deste exemplo você tenha entendido a diferença entre os dois últimos casos que explicamos, pois às vezes pode ser difícil distingui-los.

quadrado de um trinômio

Quando tentamos calcular o quadrado de um trinômio, também temos um produto notável que facilita a nossa vida. Esta expressão é representada assim: (a + b + c) ² e o produto equivalente é: a ² + b ² + c ² + 2ab + 2ac + 2bc. Ressalta-se que isso é válido no caso de um trinômio positivo, mas se um dos coeficientes for negativo basta escrever o valor negativo na fórmula. Abaixo está a demonstração da fórmula:

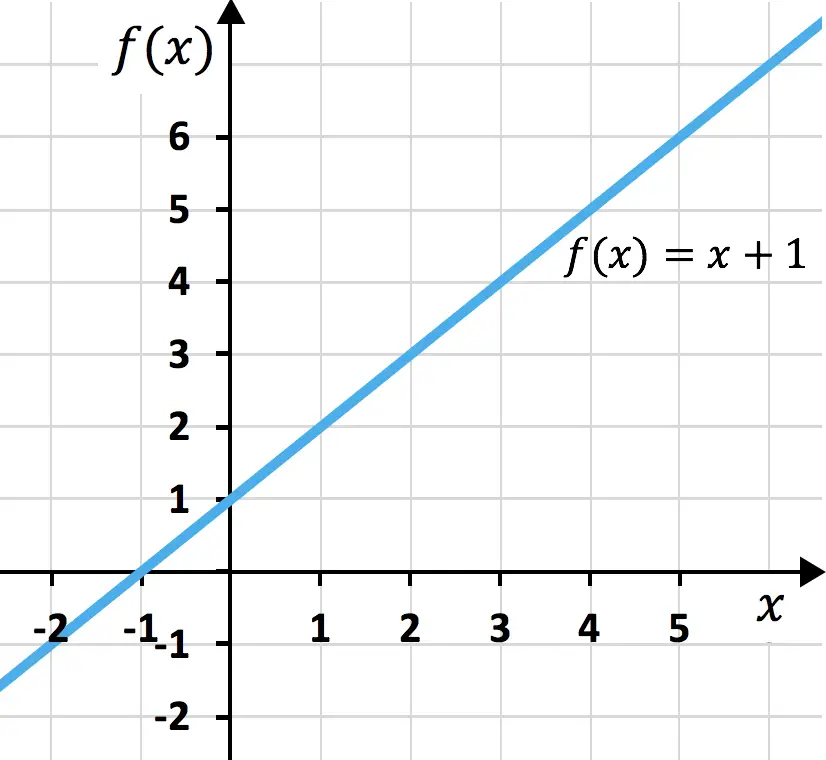
Exemplo do quadrado de um trinômio

Calcule a identidade notável (2x + 1 + x ² ) ² :

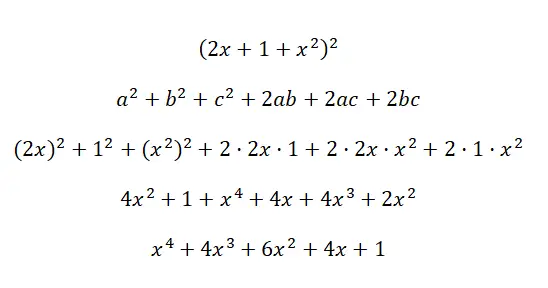
Fórmulas de identidade notáveis ou produtos em cubos notáveis

Agora que explicamos as principais identidades notáveis, veremos suas derivadas , começando pelos binômios ao cubo. Para calcular produtos notáveis deste estilo, teremos que recorrer a fórmulas um pouco mais complexas, mas que seguem uma estrutura semelhante às que já discutimos.

binômio ao cubo

O cubo de um binômio é escrito: (a + b) ³ e (a – b) ³ , esta expressão é equivalente à seguinte fórmula: (a ³ + 3a ² b + 3ab ² + b ³ ), e (a ³ – 3a ² b + 3ab ² – b ³ ). Esses dois casos são chamados de cubo de soma e cubo de subtração, porque são binômios cúbicos. Abaixo você encontrará uma demonstração bem detalhada de cada caso:

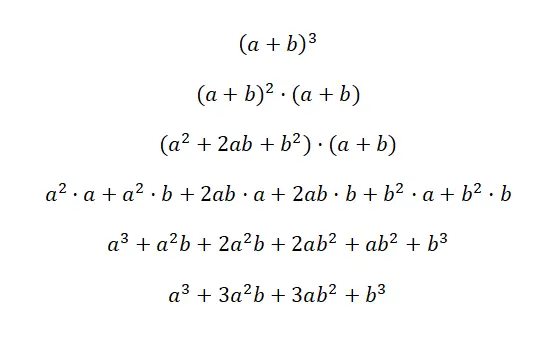
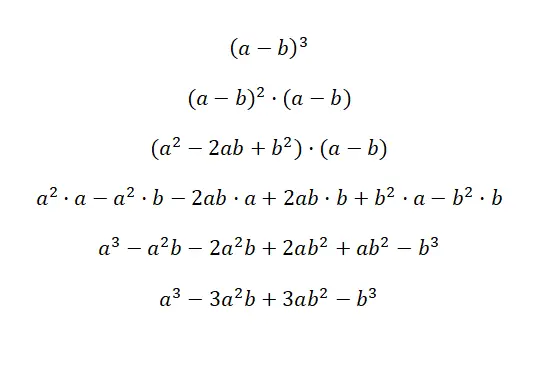
A chave para entender esta primeira prova é entender que (a + b) ³ é equivalente a: (a + b) ² · (a + b). Desta forma, utilizamos a fórmula do quadrado de uma soma , que explicamos anteriormente para multiplicar o outro fator. Então simplesmente simplificamos a expressão e obtemos a identidade notável correspondente: a ³ + 3a ² b + 3ab ² + b ³ . No caso do segundo exemplo acontece a mesma coisa, mas com mudança de sinal.

Exemplo de um cubo binomial

Resolva a identidade notável (x + 3) ³ :

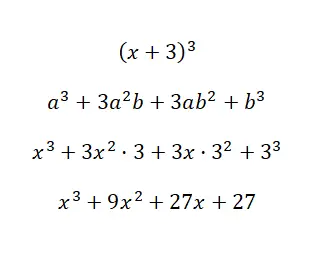
Utilizando a fórmula que acabamos de discutir, podemos calcular o polinômio, levando em consideração que: a = xyb = 3. Como você pode ver, o procedimento é muito simples e não tem muitas complicações no cálculo, é porque temos a fórmula . Caso contrário, ter que fazer tantas multiplicações seria bastante entediante.

Soma dos cubos e diferença dos cubos

Temos também este outro caso, que pode ser facilmente confundido com o anterior. Embora os dois casos sejam escritos de forma diferente, eles não são equivalentes. A expressão equivalente à soma ou diferença dos cubos é: a ³ + b ³ , enquanto no caso anterior falamos de: (a + b) ³ . Como você pode ver, há uma semelhança inegável na estrutura da expressão, mas na realidade, na hora de desenvolver o cálculo, são dois casos completamente diferentes:

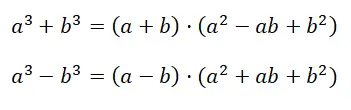
Na demonstração da fórmula obtemos a fatoração do primeiro polinômio , justamente vamos do binômio inicial ao produto de um binômio por um trinômio. Parece que o resultado obtido (a + b) · (a ² – ab + b ² ), não simplifica em nada o cálculo, mas na realidade, ao fatorar o polinômio obtemos uma expressão muito fácil de entender.

Exemplo de soma de cubos

Calcule o produto notável x ³ + 27:

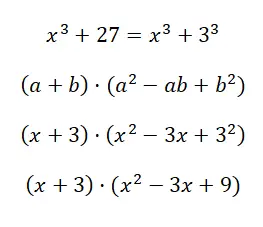
Neste caso, o resultado que obtemos é bastante longo, porque não pode ser mais simplificado. Mas, é normal chegar a esta expressão, na verdade, nestes casos só se consegue obter um resultado com a estrutura equivalente ao produto de um binômio por um trinômio, como neste exemplo.

trinômio ao cubo

O cubo de um trinômio escreve-se: (a + b + c) ³ , o que equivale a multiplicar três trinômios idênticos, mas sem expoente: (a + b + c) · (a + b + c) · (a + b +c). É o produto notável mais complexo que existe, embora a fórmula seja bastante lógica e seja obtida da mesma forma que todas, quando se realizam as correspondentes multiplicações de polinômios. Abaixo você encontrará a prova da fórmula para esta notável identidade:

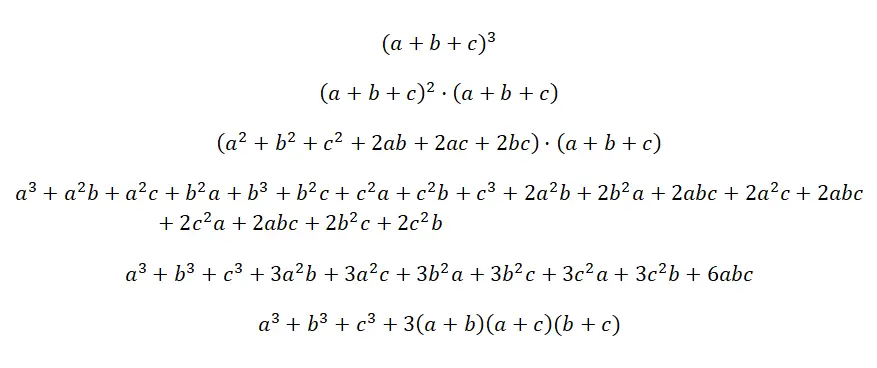
Exemplo do cubo de um trinômio

Resolva o seguinte cubo trinomial (x ² + 3x – 4) ³ :

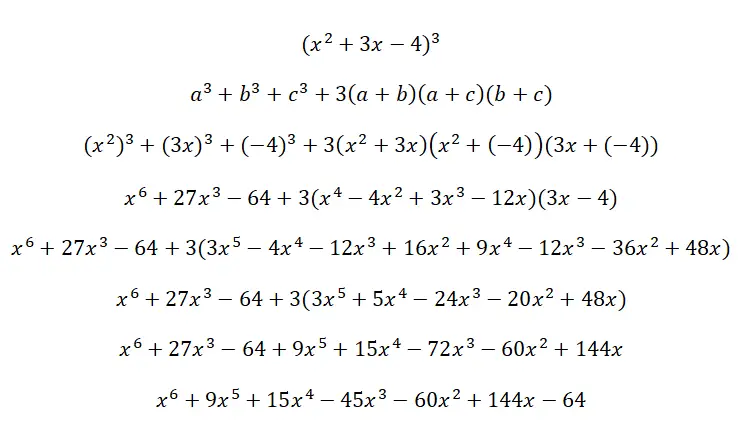
proporções notáveis

Por fim, explicaremos os quocientes notáveis , que são identidades notáveis para resolver rapidamente certos tipos de frações algébricas. Mais precisamente, existem quatro tipos diferentes, que compartilham uma característica: seu resultado é composto por polinômios exatos (com resto igual a zero). Vale ressaltar também que as fórmulas de quocientes notáveis possuem certa relação com as fórmulas de produtos notáveis que já explicamos.

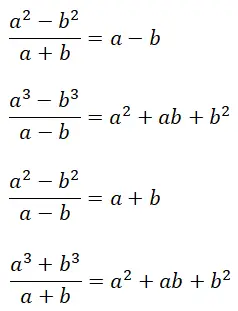
Exemplo de proporções notáveis resolvidas

Calcule as seguintes proporções notáveis:

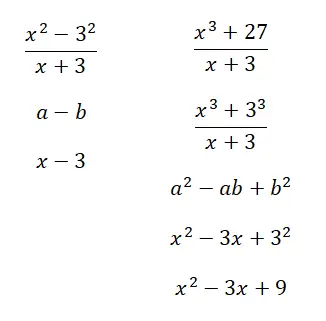
Exercícios de produtos notáveis resolvidos

Agora que você sabe como os diferentes notáveis são resolvidos, é hora de praticar um pouco. É por isso que oferecemos 6 exercícios para aplicar toda a teoria explicada. E mostramos uma tabela das principais identidades notáveis, para que você a tenha em mãos enquanto resolve todos os exercícios:

Exercício 1

Resolva os quadrados binomiais (x – 4) ² , (x + 1) ² e (x – 3) ² :

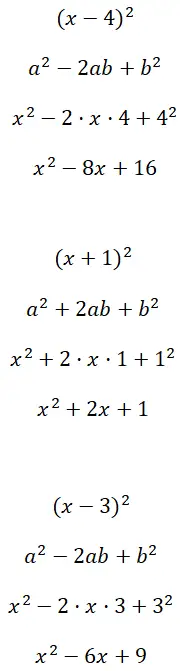
Exercício 2

Calcule as duas diferenças de quadrados (x – 1) · (x + 1) e (x + 3) · (x – 3):

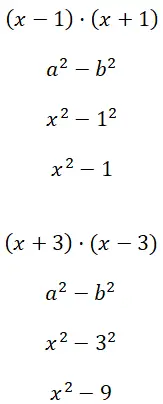
Exercício 3

Desenvolva os produtos notáveis ao cubo (x – 5) ³ e (x + 8) ³ :

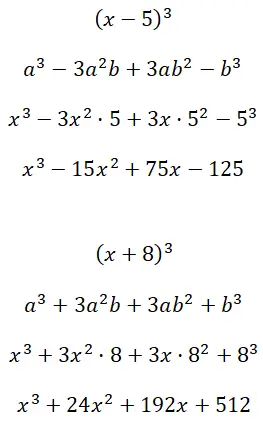
Exercício 4

Desenvolva identidades notáveis formadas a partir de termos multifatoriais (4x ² + 5y) ² , (5x ³ + y ² ) · (5x ³ – y ² ) e (5xy ² – 2xy) ² :

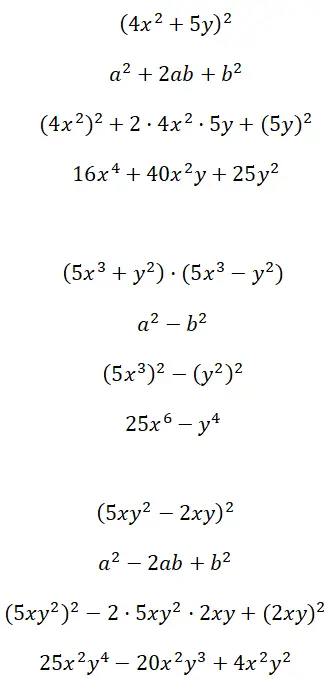
Exercício 5

Calcule os produtos cúbicos notáveis formados pelos termos multifatoriais (3x ² + y) ³ e (5y ³ – 2x ² ) ³ :

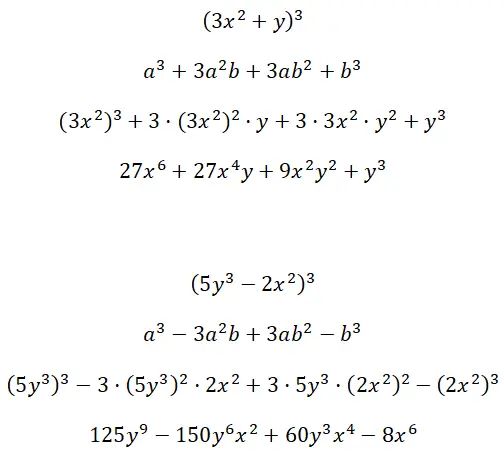
Exercício 6

Resolva os quadrados dos trinômios (2x ² + 3x + 5) ² e (3x ² + 5x + 6):