Produto vetorial de dois vetores (ou produto vetorial)

Esta página explica o que é o produto vetorial de dois vetores e como ele é calculado. Você também verá como encontrar a direção e direção do produto vetorial usando a regra da mão direita (ou saca-rolhas). E mais, você encontrará as utilizações deste tipo de operação, além de exemplos, exercícios e problemas resolvidos passo a passo.

Qual é o produto vetorial de dois vetores?

Em matemática, o produto vetorial é uma operação entre dois vetores no espaço tridimensional (em R3). O resultado desta operação vetorial é um vetor com direção perpendicular aos dois vetores multiplicados, e com módulo igual ao produto dos módulos dos vetores multiplicadores pelo seno do ângulo que eles formam. Em outras palavras, sua fórmula é:

\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)

Como você pode ver na fórmula anterior, o produto vetorial é denotado

\bm{\times}

, por isso também é chamado de produto vetorial. Às vezes também é chamado de produto vetorial de Gibbs, já que foi ele quem o inventou.

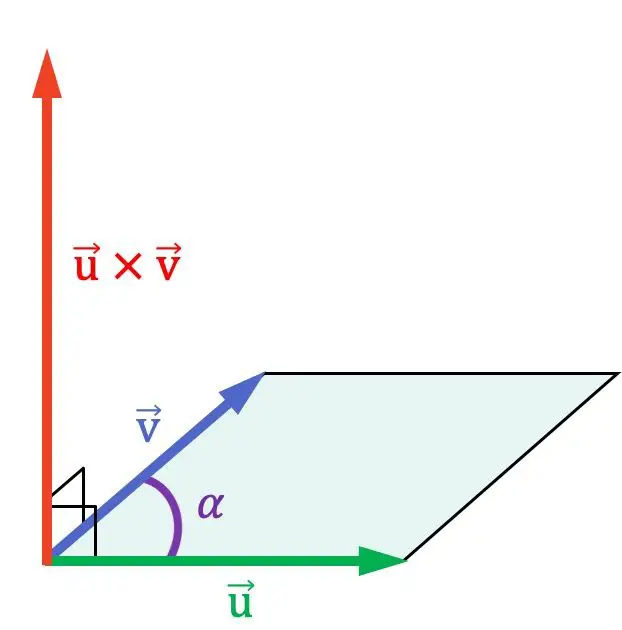
Como você pode ver na representação gráfica anterior, o produto vetorial é perpendicular aos dois vetores que eles multiplicam e, portanto, é normal ao plano que os contém.

Fórmula para calcular o produto vetorial de dois vetores

Se conhecermos as coordenadas cartesianas dos vetores, a maneira mais simples de calcular seu produto vetorial é resolver um determinante 3×3. Veja como é feito:

Considere quaisquer dois vetores:

\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)

Seu produto vetorial é:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}

Onde os vetores

\vv{i}, \vv{j},\vv{k}

Estes são os vetores unitários nas direções dos eixos X, Y e Z, respectivamente.

Vejamos um exemplo de como calcular o produto vetorial entre dois vetores:

\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)

Para determinar o produto vetorial entre os vetores, devemos fazer o seguinte determinante de ordem 3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}

Neste caso, resolveremos o determinante por adjuvantes ou cofatores (a regra de Sarrus também poderia ser usada):

\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}

O resultado do produto vetorial dos dois vetores é, portanto:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}

Determina a direção e direção do produto vetorial

Às vezes não precisamos conhecer as componentes do vetor resultante do produto vetorial, mas basta encontrar seu módulo, sua direção e seu sentido. Isso acontece frequentemente na física, especialmente no cálculo de forças.

Assim, existem diversas regras para encontrar a direção e sentido do produto vetorial, as mais conhecidas são a regra da mão direita , seja com três dedos ou com a mão inteira, e a regra do saca-rolhas (ou do parafuso) . Você pode usar qualquer uma delas, então não precisa conhecer todas, ainda vamos te explicar as três regras para que você fique com a que mais gosta. 😉

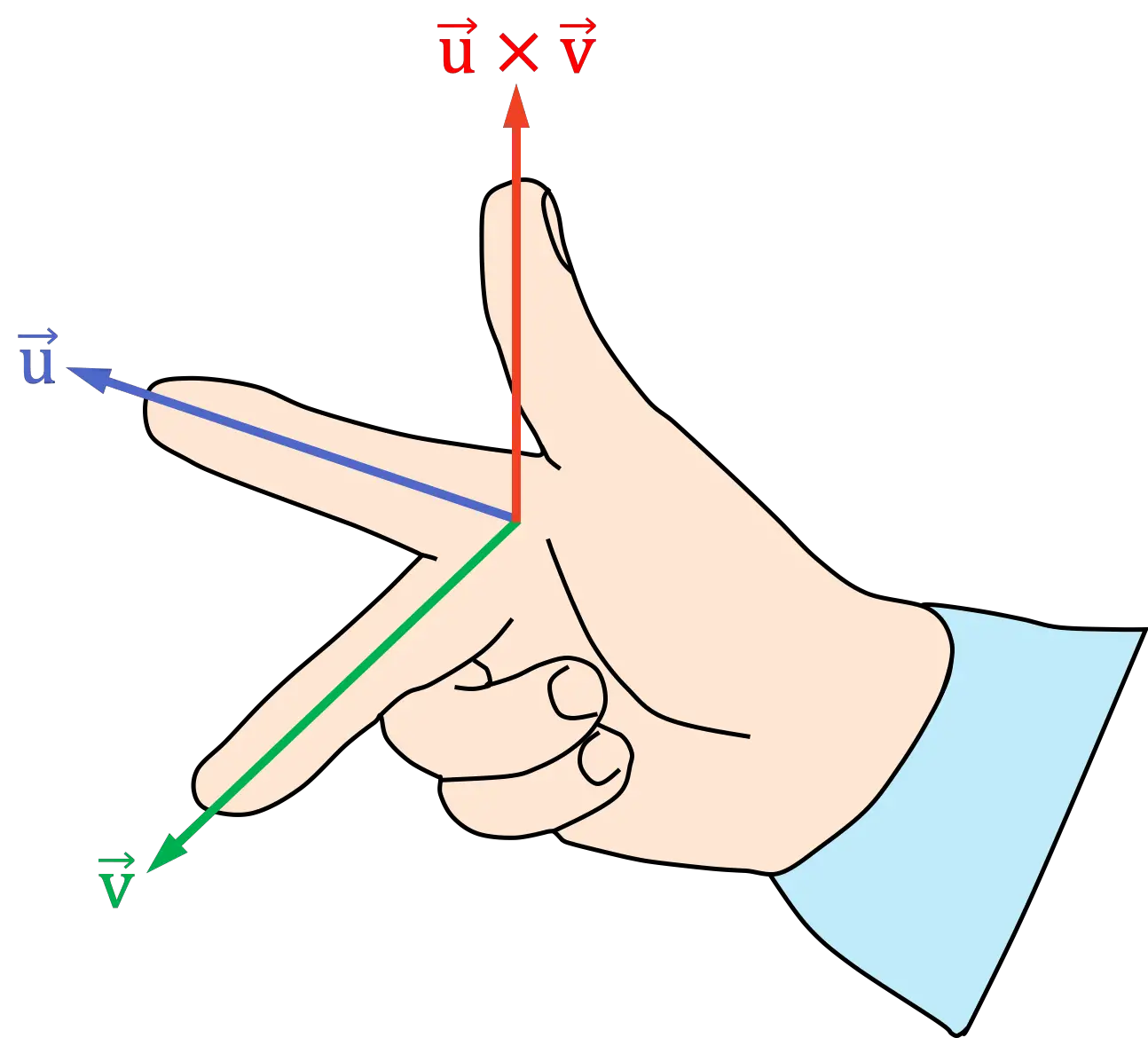
Regra da mão direita (3 dedos)

A versão de três dedos da regra ou lei da mão direita envolve a execução das seguintes etapas:

  1. Coloque o dedo indicador da mão direita em direção ao primeiro vetor do produto vetorial

    (\vv{\text{u}}).

  2. Coloque o dedo médio (ou dedo médio) da mão direita em direção ao segundo vetor do produto vetorial

    (\vv{\text{v}}).

  3. A posição do polegar resultante indica a direção e direção do produto vetorial

    (\vv{\text{u}}\times\vv{\text{v}}).

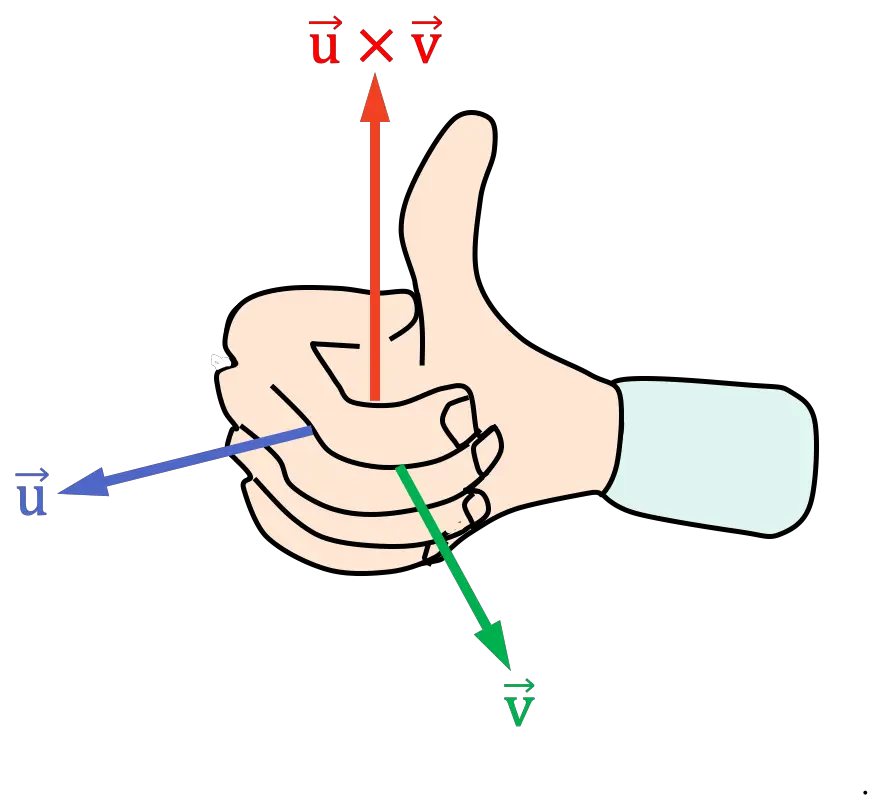
Regra da mão direita (palma da mão)

A versão palmar da regra ou lei da mão direita é muito semelhante à regra anterior. Para aplicá-lo, você deve seguir os seguintes passos:

  1. Coloque sua mão direita apontando com os dedos na mesma direção do primeiro vetor do produto vetorial

    (\vv{\text{u}}).

  2. Feche a mão direita movendo os dedos em direção ao segundo vetor do produto vetorial

    (\vv{\text{v}}).

    Você precisa fechar a mão do lado onde o ângulo (ou distância) entre os vetores é menor.

  3. A posição resultante do polegar determina a direção do produto vetorial

    (\vv{\text{u}}\times\vv{\text{v}}).

produto de vetor de régua da mão direita

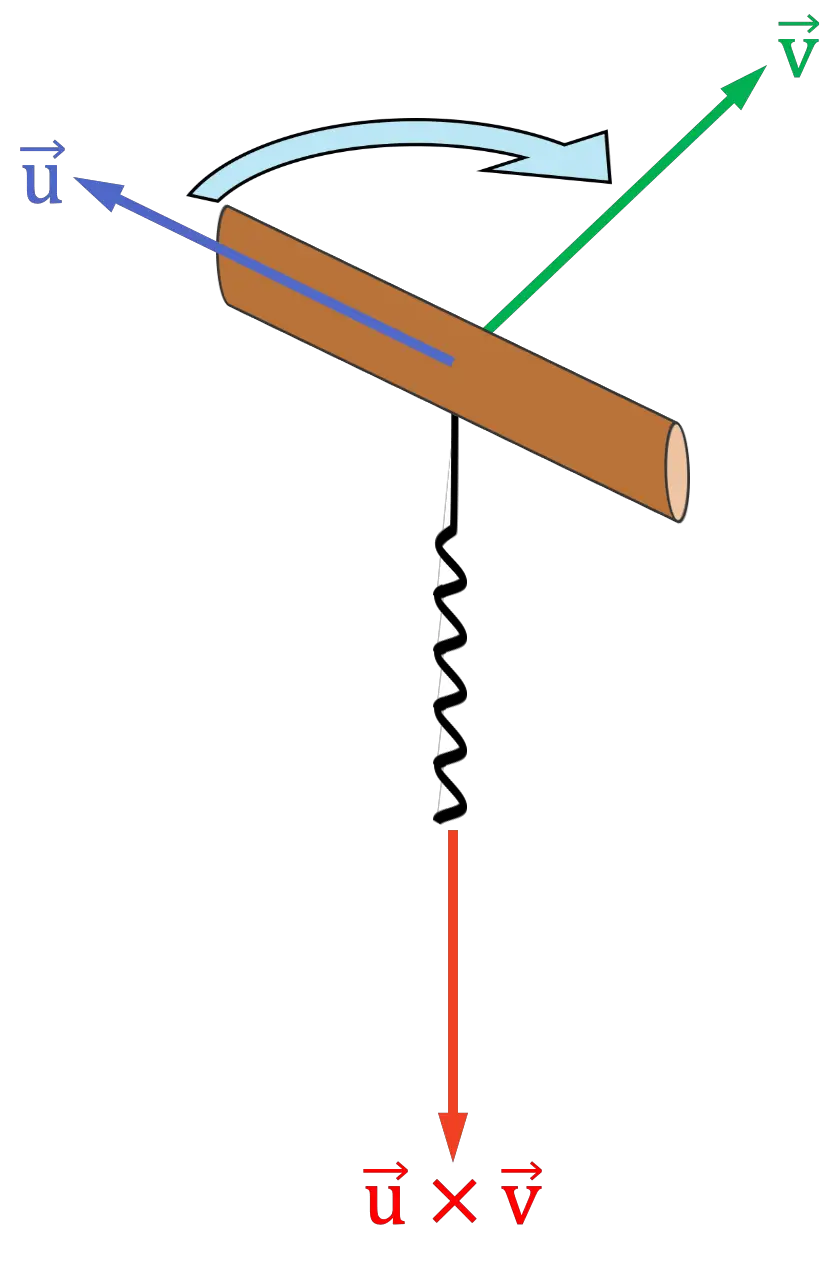
regra saca-rolhas

A regra do saca-rolhas ou parafuso é semelhante à regra da mão direita usando toda a palma da mão. O procedimento é o seguinte:

  1. Usando sua imaginação, coloque um saca-rolhas (ou parafuso) com a alça apontando na mesma direção do primeiro vetor do produto vetorial.

    (\vv{\text{u}}).

  2. Em seguida, gire o saca-rolhas em direção ao segundo vetor do produto vetorial

    (\vv{\text{v}})

    como se você fosse colocá-lo em uma rolha. Você precisa girar o saca-rolhas para o lado onde a distância entre os vetores é menor.

  3. A direção para a qual aponta a espiral do saca-rolhas será a direção e a direção do produto vetorial

    (\vv{\text{u}}\times\vv{\text{v}}).

saca-rolhas ou régua de parafuso

Propriedades do produto vetorial de dois vetores

O produto vetorial de dois vetores tem as seguintes características:

  • Propriedade anticomutativa: a ordem dos vetores envolvidos no produto vetorial não é indiferente, pois o sinal varia em função dela.

\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}

  • Propriedade distributiva relativa à adição e subtração de vetores:

\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}

\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}

  • Propriedade homogênea : multiplicar um vetor do produto vetorial por um escalar (um número real) equivale a multiplicar o resultado do produto vetorial pelo referido escalar.

k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})

  • O vetor resultante do produto vetorial é perpendicular aos dois vetores envolvidos na operação.

\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}

  • Além disso, se os dois vetores forem ortogonais, as seguintes equações serão satisfeitas:

\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}

  • O produto vetorial de dois vetores paralelos é igual ao vetor zero (ou zero).

\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0

  • Se não conhecemos o ângulo formado por dois vetores, o módulo do seu produto vetorial também pode ser calculado usando a seguinte expressão:

\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}

Calcule a área de um paralelogramo ou triângulo usando o produto vetorial

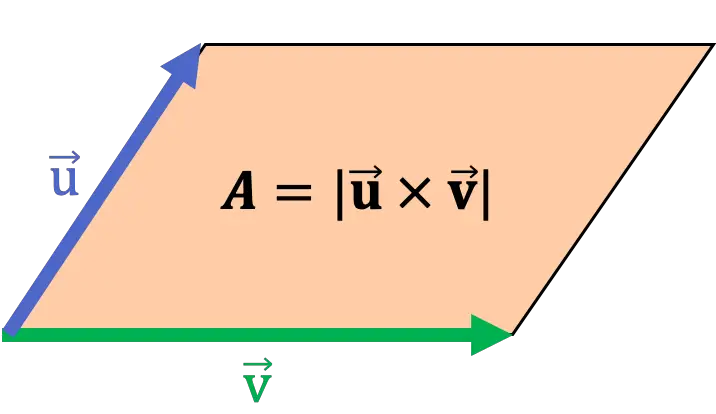
Geometricamente, o módulo do produto vetorial de dois vetores coincide com a área do paralelogramo que tem esses dois vetores como lados. Portanto, o produto vetorial pode ser usado para calcular a área de um paralelogramo.

produto vetorial de dois vetores no espaço

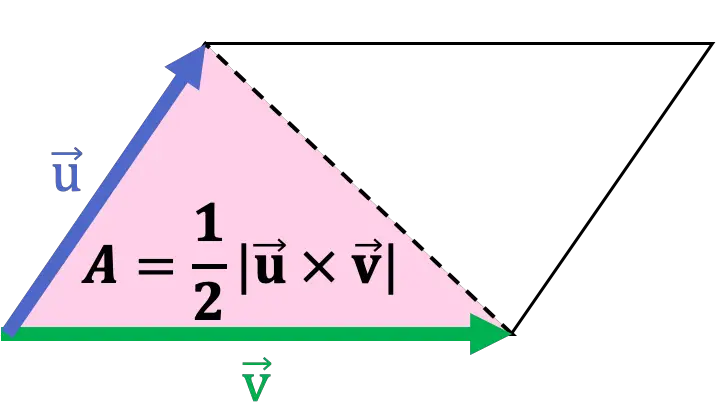
Além disso, a diagonal de um paralelogramo o divide em dois triângulos, ou em outras palavras, um triângulo é metade de um paralelogramo. Assim, a área de um triângulo é metade do módulo do produto vetorial tomando dois de seus lados como vetores.

produto vetorial de dois vetores em r2

Lembre-se de que o módulo de um vetor em um espaço tridimensional é a raiz da soma dos quadrados de suas coordenadas:

\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}

Estas são duas das aplicações do produto vetorial de dois vetores no campo da matemática. Porém, ainda tem outros usos, por exemplo, na física é usado para calcular o campo magnético.

Exercícios resolvidos sobre produtos vetoriais de vetores

Exercício 1

Calcule o produto vetorial entre os dois vetores a seguir:

\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)

Para determinar o produto vetorial entre os vetores, devemos resolver o seguinte determinante de dimensão 3×3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}

Neste caso, resolveremos o determinante por adjuvantes ou cofatores (mas a regra de Sarrus também poderia ser usada):

\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}

O resultado do produto vetorial dos dois vetores é, portanto:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}

Exercício 2

Encontre o produto vetorial entre os dois vetores a seguir:

\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)

Para encontrar o produto vetorial entre os dois vetores, devemos resolver o seguinte determinante 3×3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}

Neste caso, resolveremos o determinante por adjuntos ou cofatores (embora a regra de Sarrus possa ser usada de forma intercambiável):

\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}

O resultado do produto vetorial entre os dois vetores é, portanto:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}

Exercício 3

Conhecendo os módulos de dois vetores e o ângulo que eles formam:

|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º

Determine a magnitude do produto vetorial dos dois vetores.

Podemos calcular facilmente o módulo do produto vetorial entre os dois vetores aplicando a fórmula:

\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}

Exercício 4

Dos seguintes vetores contidos no plano da tela:

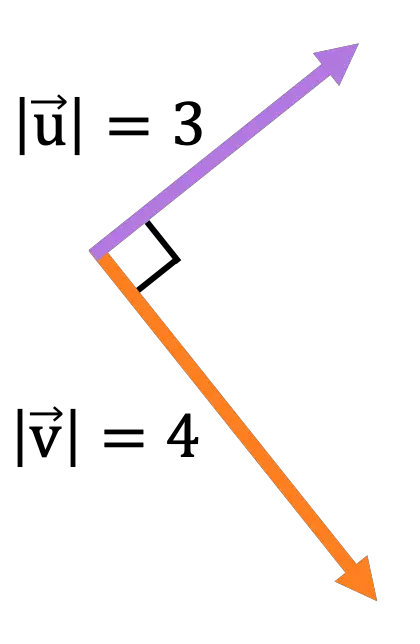
produto vetorial de dois vetores alinhados

Calcule a magnitude, direção e sentido do vetor resultante da seguinte operação vetorial:

\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert

Os dois vetores são perpendiculares, então a norma do produto vetorial será:

\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}

Por outro lado, o vetor resultante do produto vetorial é perpendicular aos dois vetores que participam da operação, sua direção será portanto perpendicular à tela.

E finalmente, utilizando a regra da reta (ou saca-rolhas), podemos deduzir que a direção do vetor resultante será para o interior da tela.

Exercício 5

Calcule a área do paralelogramo que tem os seguintes vetores como dois de seus lados:

\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)

A área de um paralelogramo coincide com o módulo do produto vetorial dos vetores que o formam. Portanto, calculamos o produto vetorial dos vetores:

\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}

E então seu módulo:

A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}

Exercício 6

Encontre a área do triângulo cujos vértices são os seguintes pontos:

A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)

Primeiramente devemos calcular os vetores que formam os lados do triângulo:

\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)

\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)

A área de um triângulo é metade da magnitude do produto vetorial dos vetores que o formam. Portanto, calculamos o produto vetorial dos vetores:

\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}

Depois do seu módulo:

\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19

E por fim, a área do triângulo será metade do módulo:

A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima