Aqui explicamos como os problemas de otimização de funções são resolvidos em etapas. Além disso, você poderá praticar com exercícios resolvidos sobre problemas de otimização.
O que são problemas de otimização?
Problemas de otimização são problemas nos quais é necessário encontrar o máximo ou o mínimo de uma função. Por exemplo, um problema de otimização envolveria o cálculo do máximo de uma função que define os lucros de uma empresa.
Como resolver problemas de otimização
Etapas para resolver problemas de otimização de função:
- Defina a função que precisa ser otimizada.
- Derive a função a ser otimizada.
- Encontre os pontos críticos da função a ser otimizada. Para fazer isso, você precisa igualar a derivada da função a zero e resolver a equação resultante.
- Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Exemplo de um problema de otimização
Considerando a teoria dos problemas de otimização, resolveremos passo a passo um problema deste tipo para que você possa ver como eles são realizados.
- Entre todos os triângulos retângulos cujos catetos totalizam 10 cm, calcule as dimensões daquele com maior área de superfície.
Para resolver o problema, chamaremos um ramo do triângulo de x e o outro ramo de y :

Passo 1: Defina a função a ser otimizada.
Queremos que a área do triângulo seja máxima, e a fórmula para a área de um triângulo é:
![]()
No nosso caso, a base do triângulo é x e sua altura é y . Ainda:
![]()
Já temos a função de otimização, mas ela depende de duas variáveis e só pode depender de uma. Porém, o enunciado nos diz que as duas pernas devem totalizar 10 cm. Ainda:
![]()
Resolvemos para y a partir desta equação:
![]()
E substituímos a expressão na função:
![]()
![]()
Agora temos a função de otimização planejada e ela depende apenas de uma variável, então podemos passar para a próxima etapa.
Passo 2: Calcule a derivada da função a ser otimizada.
É uma função racional, então aplicamos a fórmula da derivada da divisão para derivá-la:
![]()
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, precisamos igualar a derivada a zero e resolver a equação resultante:
![]()
![]()
O 4 divide todo o lado esquerdo, então podemos multiplicar multiplicando todo o lado direito:
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Para estudar a monotonia da função, representamos o ponto crítico encontrado à direita:
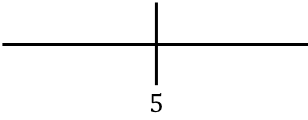
E agora avaliamos o sinal da derivada em cada intervalo para descobrir se a função é crescente ou decrescente. Para fazer isso, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem naquele ponto:
![]()
![]()
![]()
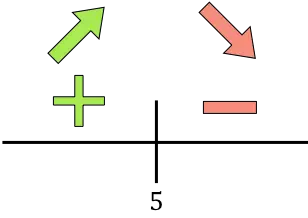
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos para aumentar e diminuir a função são:
Crescimento:
![]()
Diminuir:
![]()
Em x=5 a função vai de crescente para decrescente, então x=5 é um máximo relativo da função a ser otimizada .
Portanto, x=5 é o valor do ramo do triângulo que possui a área máxima. Basta calcular o valor da outra perna:
![]()
Concluindo, os valores que maximizam a área máxima do triângulo são:
![]()
![]()
Problemas de otimização resolvidos
Problema 1
O medicamento é dado a uma pessoa doente e
![]()
algumas horas depois, a concentração sanguínea do princípio ativo é dada pela função
![]()
miligramas por mililitro. Determine o valor máximo de
![]()
e indica quando esse valor é alcançado.
Passo 1: Defina a função a ser otimizada.
Neste problema, eles já nos dão a função proposta, que é
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
A função é composta pelo produto de 2 funções. Portanto, para calcular a derivada da função, devemos aplicar a regra para a derivada de um produto:
![]()
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
Tomamos o fator comum para resolver a equação:
![]()
Para que a multiplicação seja igual a 0, um dos dois elementos da multiplicação deve ser zero. Portanto, definimos cada fator igual a 0:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Um número elevado a outro número nunca pode dar 0, portanto,
![]()
Não há solução.
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Para estudar a monotonia da função, representamos o ponto crítico encontrado à direita:
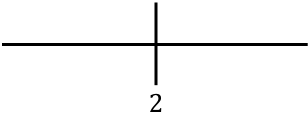
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
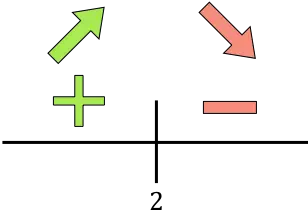
Se a derivada for positiva significa que a função aumenta, por outro lado se a derivada for negativa significa que a função diminui. Assim os intervalos de crescimento e diminuição da função a ser otimizada são:
Crescimento:
![]()
Diminuir:
![]()
A função vai de crescente a decrescente em t=2, então t=2 é o máximo da função. A concentração máxima será, portanto, alcançada em t=2 horas.
Finalmente, substituímos o valor em que ocorre o máximo na função original, para encontrar o valor da concentração máxima:
![]()
Problema 2
Uma loja espera vender 40 scooters elétricas ao preço de 1.000 euros por scooter. Mas, de acordo com estudos de mercado, por cada redução de 50€ no preço das scooters, haverá um aumento nas vendas das 10 scooters mais vendidas.
Primeiro, escreva a função de receita da loja com base no número de vezes que o preço original de US$ 1.000 da scooter é reduzido em US$ 50. Em seguida, determine o preço da scooter para obter o lucro máximo e a receita obtida com esse preço.
Passo 1: Defina a função a ser otimizada.
A definição do problema nos dá uma pista, pois nos diz que a função deve depender do número de vezes que o preço inicial é reduzido em US$ 50. Chamaremos, portanto, de x o número de vezes que o preço é reduzido em 50€:
![]()
€
A função receita será o número de scooters vendidas multiplicado pelo preço de cada scooter:
![]()
O número de scooters vendidas será de 40 mais 10 scooters por cada redução de preço de 50€. Ainda:
![]()
O preço de cada scooter será de 1000€ no início e diminuirá 50€ a cada descida de preço. Ainda:
![]()
A função para otimizar o problema é, portanto:
![]()
![]()
![]()
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
Por ser uma função polinomial, a derivada é mais fácil de calcular:
![]()
Etapa 3: Encontre os pontos críticos da função.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Para estudar a monotonicidade da função, representamos o ponto crítico calculado na reta numérica:
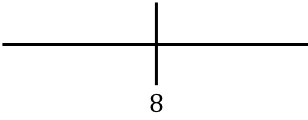
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
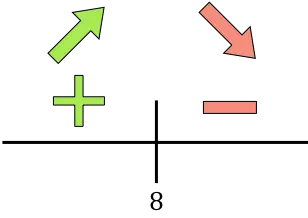
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos de crescimento e declínio são:
Crescimento:
![]()
Diminuir:
![]()
A função vai de crescente a decrescente em x=8, então x=8 é o máximo da função. Portanto, o rendimento máximo será obtido fazendo 8 vezes a redução de 50€.
Substituímos agora o valor em que o rendimento máximo aparece na função original, para encontrar o valor do rendimento máximo:
![]()
![]()
€
E o preço de cada scooter depois de ter feito o desconto de 50€ 8 vezes será:
![]()
![]()
€
Problema 3
A função custo (em milhares de euros) de uma empresa pode ser determinada através da seguinte expressão:
![]()
Ouro
![]()
representa os milhares de unidades produzidas de um determinado item.
Determine quanto deve ser produzido para que o custo seja mínimo, qual é esse custo e qual seria o custo se nenhum desses itens fosse produzido.
Passo 1: Defina a função a ser otimizada.
A declaração do problema já nos fornece a função a ser otimizada, que é
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Representamos o ponto crítico encontrado à direita:
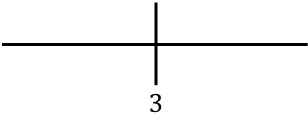
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
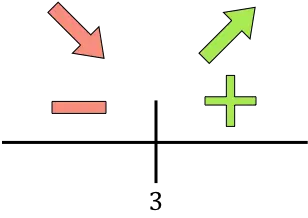
Se a derivada for maior que zero, a função aumenta nesse intervalo. Por outro lado, se a derivada for menor que zero, a função diminui neste intervalo. Assim, os intervalos de aumento e diminuição da função são:
Crescimento:
![]()
Diminuir:
![]()
A função vai de decrescente para crescente em x=3, então x=3 é o mínimo da função. Portanto, o custo mínimo será alcançado com a produção de 3.000 unidades.
Agora substituímos o valor pelo qual o custo mínimo é alcançado na função original para encontrar o valor do custo mínimo:
![]()
milhões de euros.
Por outro lado, perguntam-nos qual seria o custo se nada fosse produzido, ou seja, quando
![]()
É necessário, portanto, calcular
![]()
![]()
milhões de euros.
Problema 4
Queremos construir uma moldura retangular de madeira que delimite uma área de 2 m 2 . Sabemos que o preço da madeira é de 7,5€/m para as laterais horizontais e de 12,5€/m para as laterais verticais. Determine as dimensões que o retângulo deve ter para que o custo total da moldura seja o mínimo possível e esse custo seja mínimo.
Passo 1: Defina a função a ser otimizada.
Para resolver o problema, chamaremos o lado horizontal de x e o lado vertical de y :

Comprar um lado horizontal custa 7,5€ e comprar um lado vertical custa 12,5€. Além disso, para cada quadro precisamos de dois lados horizontais e dois lados verticais. Portanto, o custo do quadro pode ser determinado com a seguinte função:
![]()
Já temos a função de otimizar. Mas depende de duas variáveis quando só pode depender de uma. Porém, o comunicado diz-nos que a superfície da moldura deve ser de 2 m 2 . Ainda:
![]()
Excluímos a variável y :
![]()
E substituímos a expressão encontrada na função a ser otimizada:
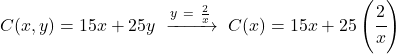
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
![]()
![]()
![]()
Multiplicamos transversalmente para resolver a equação com frações:
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Representamos o ponto crítico encontrado para analisar a monotonia da função na reta:
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos de crescimento e declínio são:
Crescimento:
![]()
Diminuir:
![]()
A função muda de decrescente para crescente em x=1,83, então x=1,83 é o mínimo da função.
Portanto, x=1,83 é o valor do lado horizontal que representa o custo mínimo. Agora vamos calcular o valor do lado vertical:
![]()
Assim, os valores que compõem o custo mínimo do enquadramento são:
lado horizontal
![]()
lado vertical
![]()
E o custo mínimo alcançado com estes valores é:
![]()
€
Problema 5
A porta de uma catedral é formada por um arco semicircunferencial sustentado por duas colunas, conforme mostra a figura a seguir:
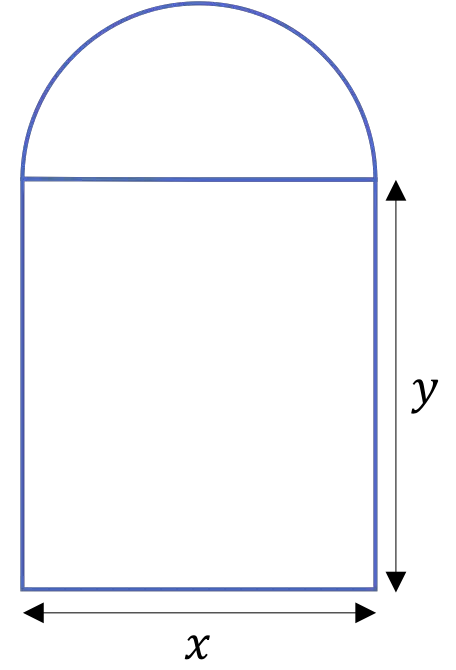
Se o perímetro da porta for 20 m, determine as medidas
![]()
E
![]()
o que maximiza a área de superfície de toda a porta.
Passo 1: Defina a função a ser otimizada.
A área de um círculo é calculada pela fórmula
![]()
Portanto, a área de toda a porta será a área do retângulo mais metade da área da circunferência:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
Já temos a função de otimizar. Mas depende de duas variáveis quando só pode depender de uma.
Porém, o comunicado informa que o perímetro de todo o portão é de 20m. O perímetro de um círculo é calculado pela fórmula
![]()
Portanto, o perímetro de toda a porta será:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
O perímetro deve ser de 20 m. Portanto, definimos a expressão anterior igual a 20 para encontrar a relação entre
![]()
E
![]()
![]()
Multiplicamos todos os termos por 2 para eliminar frações:
![]()
![]()
Nós limpamos
![]()
![]()
![]()
E substituímos a expressão encontrada na função a ser otimizada:
![]()
![]()
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
![]()
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
Esta é uma equação com frações, então multiplicamos cada termo pelo lcm dos denominadores para eliminar as frações:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Para estudar a monotonia da função, representamos o ponto crítico encontrado à direita:
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
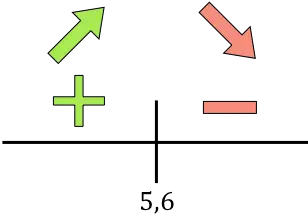
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos de crescimento e declínio são:
Crescimento:
![]()
Diminuir:
![]()
A função vai de crescente a decrescente em x=5,6, então x=5,6 é o máximo da função.
Ainda,
![]()
é o valor que constitui a superfície máxima. Agora calculamos o valor de
![]()
![]()
Assim, os valores que compõem a superfície máxima são:
![]()
![]()
Problema 6
Queremos construir um tanque em forma de cilindro com área de 54 cm 2 . Determine o raio da base e a altura do cilindro para que o volume seja máximo.
Passo 1: Defina a função a ser otimizada.
O volume de um cilindro é calculado pela seguinte fórmula:
![]()
A área da base é um círculo, então sua fórmula é
![]()
. A fórmula para o volume do cilindro é, portanto:
![]()
Já temos a função de otimizar. Mas depende de duas variáveis (
![]()
E
![]()
) embora só possa depender de um. Porém, o enunciado nos diz que a área do cilindro deve ser 54 cm 2 , então aproveitaremos esta condição para encontrar a relação entre
![]()
E
![]()
Para calcular a área de um cilindro você deve somar sua área lateral com as áreas das duas bases:
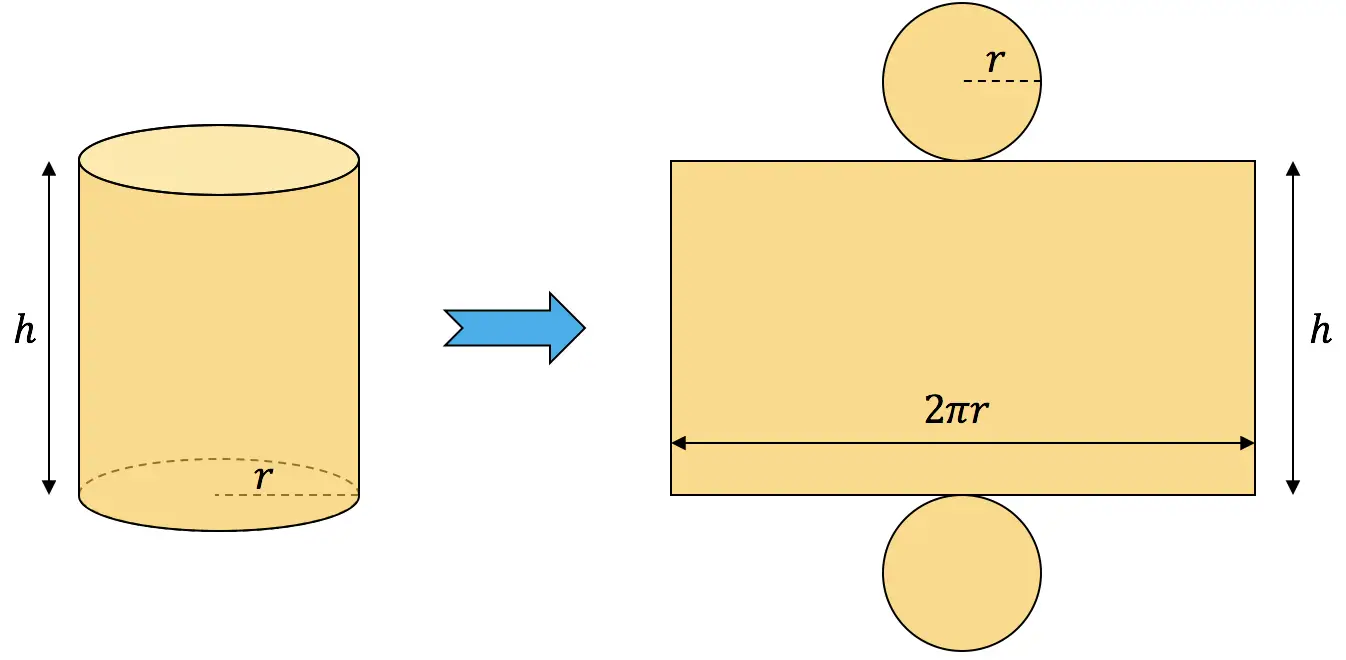
![]()
A área do cilindro deve ser 54 cm 2 , então igualamos a expressão anterior a 54 para obter a relação entre
![]()
E
![]()
![]()
Nós limpamos
![]()
![]()
![]()
E substituímos a expressão encontrada na função a ser otimizada:
![]()
![]()
![]()
Passo 2: Calcule a derivada da função a ser otimizada.
![]()
Etapa 3: Encontre os pontos críticos.
Para encontrar os pontos críticos da função, resolvemos
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Passo 4: Estude a monotonicidade da função e determine o máximo ou mínimo da função.
Para estudar a monotonicidade da função, representamos o ponto crítico encontrado na reta numérica:
E agora avaliamos o sinal da derivada em cada intervalo, para descobrir se a função é crescente ou decrescente. Portanto, pegamos um ponto em cada intervalo (nunca o ponto crítico) e observamos qual sinal a derivada tem neste ponto:
![]()
![]()
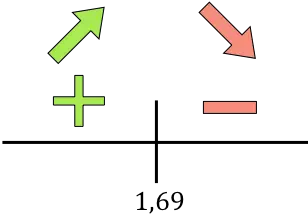
Se a derivada for positiva, significa que a função está aumentando, e se a derivada for negativa, significa que a função está diminuindo. Portanto, os intervalos de crescimento e declínio são:
Crescimento:
![]()
Diminuir:
![]()
A função vai de crescente para decrescente em r=1,69, então r=1,69 cm é o máximo da função.
Portanto, r=1,69 é o valor do raio que perfaz o volume máximo. Agora calculamos a altura:
![]()
Então os valores que fazem o volume máximo são:
Rádio
![]()
Altura
![]()