Posições relativas de uma reta e de um plano

Nesta página você encontrará as posições relativas de uma linha e de um plano. Explicamos como se calcula a posição relativa entre uma reta e um plano (2 métodos) e, além disso, você poderá ver exemplos e exercícios resolvidos passo a passo.

Quais são as posições relativas entre uma linha e um plano?

Antes de examinar todas as posições relativas possíveis entre uma reta e um plano, obviamente precisamos saber o que são retas e o que é um plano . Portanto, se você ainda não tem esses dois conceitos muito claros, recomendamos que primeiro dê uma olhada nas páginas vinculadas onde eles são explicados detalhadamente.

Assim, na geometria analítica, existem apenas três posições relativas no espaço entre uma linha e um plano:

Reta contida no plano : quando a reta está contida no plano significa que elas possuem um número infinito de pontos em comum.
Reta e plano paralelos : Uma reta e um plano são paralelos quando não têm ponto em comum.
Intersecção entre linha e plano : Uma linha e um plano se cruzam quando a linha intercepta o plano em um ponto. Então eles só têm uma coisa em comum.

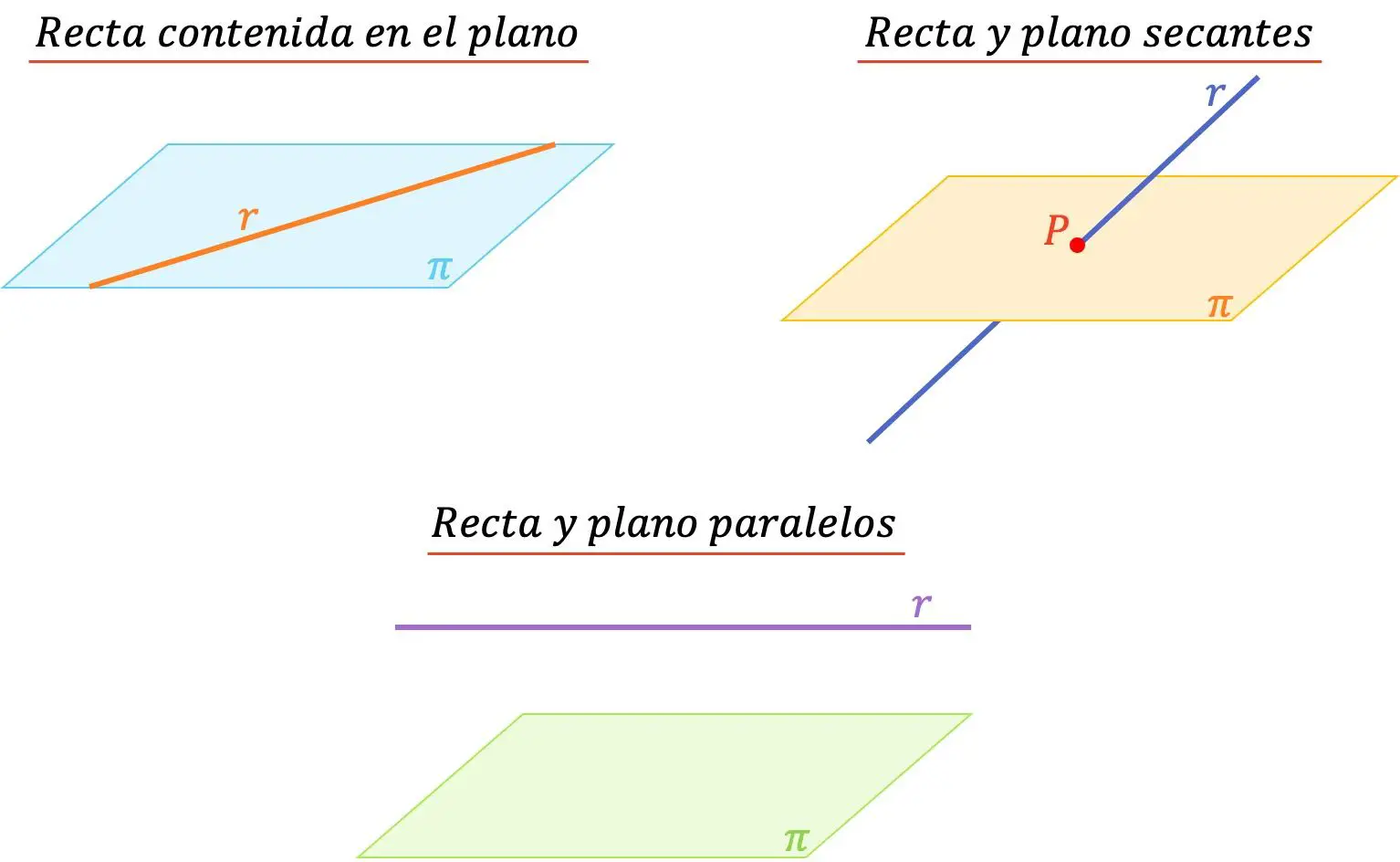
Por outro lado, quando a reta está contida no plano ou quando são paralelas entre si, o ângulo que formam será 0º. Por outro lado, quando a reta e o plano se cruzam, o ângulo entre os dois elementos geométricos pode variar de 0º (não incluído) a 90º (inclusive).

Como calcular a posição relativa de uma linha e de um plano?

Existem principalmente dois métodos para encontrar a posição relativa entre uma linha e um plano no espaço: por intervalos ou por vetores .

Quando a reta é expressa como uma equação implícita (ou geral), é mais fácil usar o método de classificação. Por outro lado, se a reta for dada com outro tipo de equação, por exemplo quando estiver na forma de uma equação vetorial, paramétrica ou contínua, é mais rápido utilizar o método vetorial.

Se você não se lembra como são as equações da reta, deixamos uma página onde você pode consultar todas as equações da reta . Aqui você encontrará todas as equações da reta, uma fórmula para encontrar rapidamente a equação de uma reta que passa por dois pontos, exemplos e exercícios resolvidos passo a passo.

Portanto, é mais prático utilizar um método ou outro dependendo do problema, por isso recomendamos que você saiba fazer os dois procedimentos. Abaixo está a explicação de ambos os métodos com exemplos.

Quando a reta está na forma de uma equação implícita (ou geral)

Uma maneira de determinar a posição relativa entre uma linha e um plano é calcular a classificação de duas matrizes.

Se a reta for definida por suas equações implícitas (ou gerais):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

E o plano também é expresso na forma de uma equação geral:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Chamaremos de A a matriz composta pelos coeficientes A, B e C das equações do plano e da reta:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

E a matriz A’ será a matriz expandida com todos os coeficientes das duas equações:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Então, a posição relativa entre a reta e o plano é determinada pelo valor da extensão das duas matrizes anteriores de acordo com a tabela a seguir:

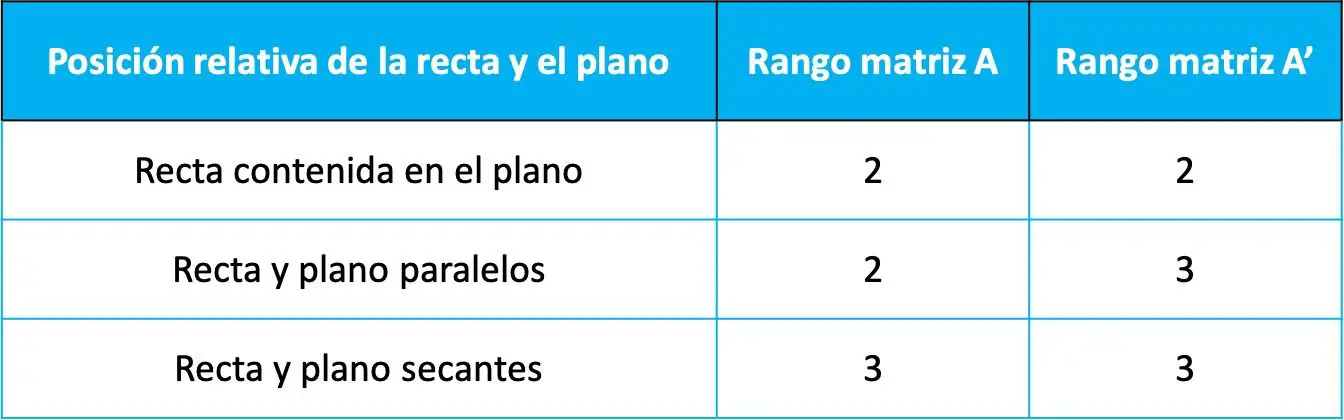
estudar a posição relativa entre uma linha e um plano no espaço por intervalos

Que as posições relativas dependem das classificações dessas duas matrizes pode ser mostrado no toerem de Rouche-Frobenius (um teorema usado para resolver sistemas de equações lineares). Porém, nesta página não faremos a demonstração porque não é necessário conhecê-la e também não fornece muita coisa.

Exemplo de como encontrar a posição relativa de uma linha e um plano por intervalos

Para que você veja exatamente como isso é feito, vamos resolver um exercício como exemplo:

Estude a posição relativa entre a seguinte linha e o seguinte plano:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

A reta é definida por dois planos que se cruzam, ou seja, é expressa como uma equação implícita. Portanto, usaremos o método de classificação para estudar a posição relativa entre a reta e o plano.

A primeira coisa a fazer é construir a matriz A e a matriz estendida A’ com os coeficientes das equações:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

E agora precisamos calcular a classificação de cada matriz. Primeiro encontramos a extensão da matriz A por determinantes:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

O determinante da matriz A é zero, mas contém uma submatriz 2×2 cujo determinante é diferente de zero, portanto é uma matriz de posto 2.

Por outro lado, também é necessário calcular o posto da matriz A’. E o contradomínio da matriz estendida A’ será sempre pelo menos igual ao da matriz A, então só precisamos verificar se ela é de posto 3 ou 2:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Por outro lado, a matriz estendida A’ possui um subdeterminante 3×3 diferente de 0, sendo portanto de posto 3.

Portanto, como a matriz A é de posto 2 e a matriz A’ é de posto 3, a reta e o plano são paralelos .

Quando a reta está na forma de outro tipo de equação

Quando a reta é expressa por uma equação diferente da implícita, seja a equação vetorial, paramétrica ou contínua, é preferível utilizar o método que explicamos a seguir.

Assim, se a reta é dada na forma de uma equação vetorial, de equações paramétricas ou de uma equação contínua, significa que conhecemos um ponto que pertence à reta e, também, seu vetor diretor.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

Por outro lado, também sabemos qual é o vetor normal (ou perpendicular) ao plano:

$\vv{n} \perp \pi$

Então, a partir dos 2 vetores e do ponto da reta, a posição relativa entre a reta e o plano pode ser calculada da seguinte forma:

Se o produto escalar entre o vetor diretor da reta e o vetor normal ao plano for diferente de zero, isso significa que a reta é secante ao plano.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
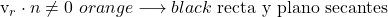
Mas se o produto escalar entre o vetor diretor da reta e o vetor normal ao plano for igual a zero, existem duas possibilidades: a reta está contida no plano ou são paralelos. E para saber qual é o caso, devemos substituir as coordenadas de um ponto da reta na equação do plano.
- Se o ponto satisfaz a equação do plano, a reta está contida no plano.
- Por outro lado, se o ponto não satisfaz a equação do plano, a reta e o plano são paralelos.

Exemplo de determinação da posição relativa de uma linha reta e de um plano usando vetores

Depois de vermos a teoria deste método, vamos agora ver um exercício resolvido passo a passo:

Encontre a posição relativa entre a seguinte linha e o seguinte plano:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Primeiro, a reta é definida como equações paramétricas, então seu vetor de direção e um ponto pelo qual ela passa são:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

E, por outro lado, o vetor normal ao plano é:

$\vv{n} =(2,1,-2)$

Uma vez conhecido o vetor diretor da reta e o vetor normal ao plano, devemos calcular o produto escalar entre os dois:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

O resultado do produto escalar é zero, então a reta só pode estar contida no plano ou ser paralela a ele. Então, para descobrir qual é o caso, substituímos as coordenadas cartesianas do ponto da reta na equação do plano:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Substituindo o ponto da reta na equação do plano obtemos uma igualdade, pois o ponto respeita a equação do plano e, consequentemente, a reta está contida no plano .

Posições relativas de uma linha e de um plano