Posição relativa de duas linhas no espaço

Aqui você encontrará todas as posições relativas de duas linhas no espaço (em R3). Além disso, explica como encontrar a posição relativa entre duas retas utilizando os 2 métodos possíveis: por intervalos ou a partir de um ponto e um vetor de cada reta. Você ainda poderá ver exemplos e exercícios resolvidos passo a passo.

Quais são as posições relativas de duas linhas no espaço?

Na geometria analítica, ao trabalhar num espaço tridimensional (em R3) existem 4 posições relativas possíveis entre duas retas: duas retas podem ser retas mescladas , retas paralelas , retas secantes ou retas secantes .

Linhas paralelas

Duas linhas são paralelas se têm a mesma direção, mas não têm ponto comum. Além disso, as linhas paralelas estão sempre à mesma distância umas das outras.

linhas coincidentes

Duas retas coincidem se tiverem a mesma direção e, além disso, se todos os seus pontos forem comuns.

linhas que se cruzam

Duas linhas que se cruzam têm direções diferentes, mas se tocam em um ponto.

Linhas de interseção

Duas linhas que se cruzam têm direções diferentes e não se cruzam em nenhum ponto. Portanto, duas linhas cruzadas não estão no mesmo plano. Por exemplo, na representação gráfica acima da linha

$s$

está sempre à frente da linha

$r$

, então eles nunca se tocarão.

Existem 2 maneiras de saber qual é a posição relativa entre duas retas, pois dependem de como as equações das duas retas são expressas:

Se as retas estiverem na forma vetorial, paramétrica ou de equação contínua, é melhor calcular a posição relativa a partir de um ponto e um vetor de cada reta (a explicação deste método é dada abaixo).
Por outro lado, se as retas forem definidas na forma de equações implícitas (ou gerais), é mais fácil saber a posição relativa entre as duas retas calculando o posto de duas matrizes (veja a explicação abaixo).

Determinando a posição relativa de duas linhas de um ponto e um vetor

Você pode descobrir qual posição relativa existe entre duas retas com um ponto e um vetor de cada reta. Este método é apropriado para uso quando as retas são definidas na forma de uma equação vetorial, equações paramétricas ou uma equação contínua.

Assim, seja o vetor diretor e qualquer ponto em cada uma das duas retas:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Portanto, para encontrar a posição relativa de duas retas, precisamos seguir o seguinte procedimento:

‣ A primeira coisa que precisamos fazer é ver se os vetores das duas retas são proporcionais ou não e, dependendo do caso, fazemos o seguinte:

Se os dois vetores forem proporcionais, as retas podem ser paralelas ou coincidir. Devemos, portanto, verificar se o ponto de uma reta satisfaz a equação da outra reta:
- Se o ponto de uma reta satisfaz a equação da outra reta, significa que as duas retas coincidem.
- Caso contrário, isso implica que as duas linhas são paralelas.
Se os dois vetores não forem proporcionais, as linhas podem estar se cruzando ou se cruzando. Neste caso devemos resolver o seguinte determinante 3×3:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Se o determinante anterior for igual a zero, as duas retas se cruzam em um ponto (elas se cruzam).
- Se o determinante anterior for diferente de zero, as duas retas se cruzam.

O gráfico a seguir resume todo o procedimento:

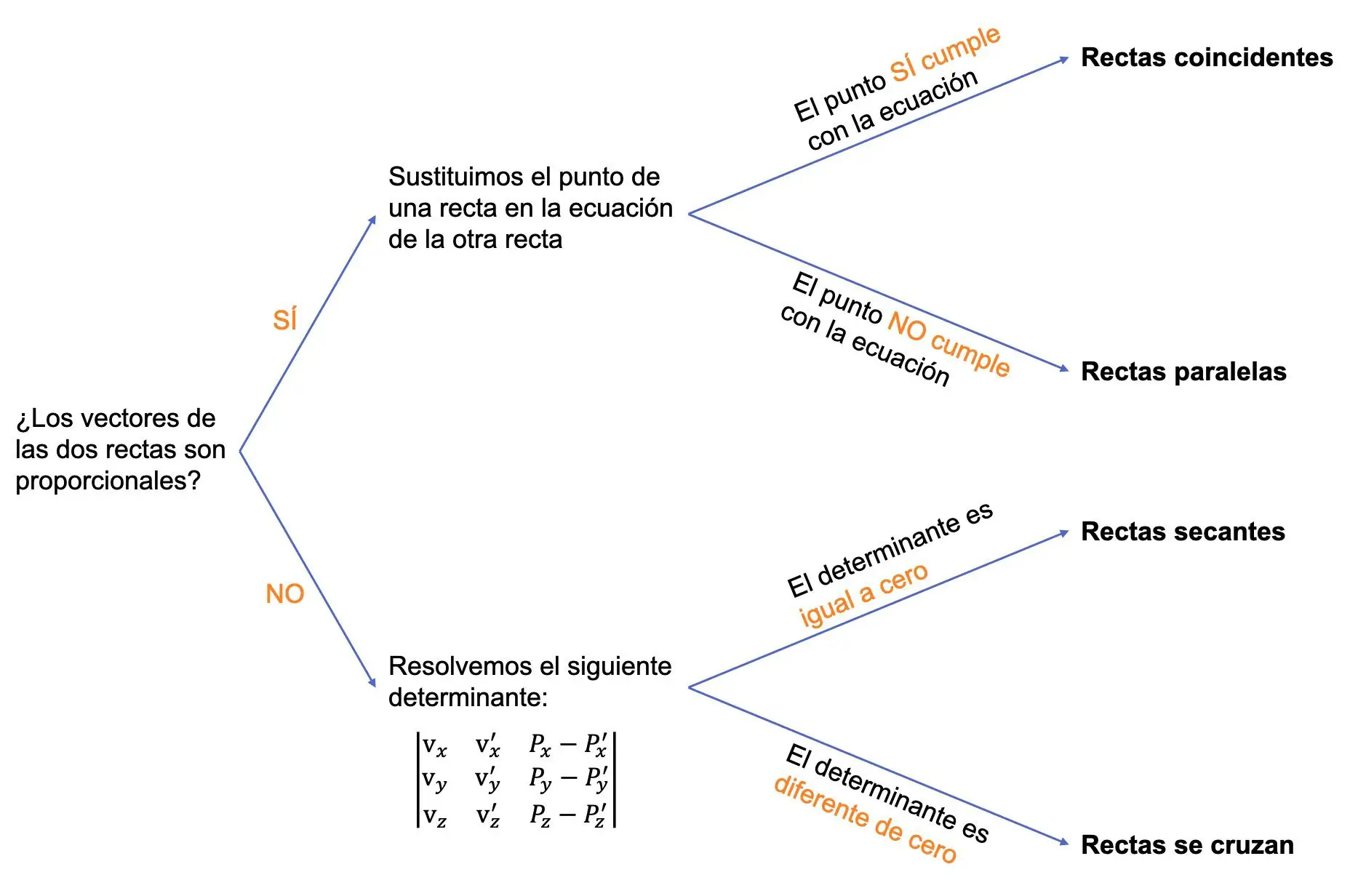
Exemplo de determinação da posição relativa entre duas linhas

O procedimento anterior pode parecer um pouco complicado, mas para que você veja que é o contrário, resolveremos um problema como exemplo:

Determine a posição relativa entre as duas linhas a seguir:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

As duas retas são expressas como uma equação vetorial, com a qual o vetor de direção de cada reta é:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

E um ponto pelo qual cada linha passa é:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Depois de conhecermos um ponto e o vetor de direção de cada reta, aplicamos o método visto acima. Primeiramente devemos verificar se as coordenadas dos vetores são proporcionais:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Como os dois vetores não são proporcionais entre si, as linhas só podem tocar-se ou cruzar-se. Portanto, precisamos agora resolver o seguinte determinante formado pelo vetor diretor e um ponto em cada reta:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Substituímos os valores na fórmula:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

E calculamos o determinante, para isso você pode usar qualquer método (regra de Sarrus, método dos complementos ou cofatores, etc.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Se o resultado da determinação tivesse sido zero, isso significaria que as linhas se cruzam (tocam). Mas o determinante é diferente de 0, então as retas se cruzam .

Encontre a posição relativa de duas linhas por linhas

Outra forma de encontrar a posição relativa de duas linhas é calcular os postos de duas matrizes concretas, como veremos a seguir. Este método é muito útil quando as duas retas estão na forma de equação implícita (ou geral).

Portanto, se tivermos duas retas expressas com suas equações implícitas (ou gerais) em um espaço tridimensional (em R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Seja A a matriz composta pelos coeficientes das duas retas:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

E dada a matriz estendida A’, que é a matriz formada por todos os parâmetros das duas linhas:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Então, a posição relativa das duas linhas pode ser determinada pelo contradomínio das duas matrizes anteriores de acordo com a tabela a seguir:

posições relativas de duas linhas por linhas

Portanto, para encontrar a posição relativa entre duas linhas teremos que calcular os postos das duas matrizes e dependendo do posto de cada matriz será um caso ou outro.

Este teorema pode ser provado usando o teorema de Rouché-Frobenius (método usado para resolver sistemas de equações lineares), porém nesta página não faremos a prova porque é bastante complicado e não acrescenta muito.

Exemplo de como encontrar a posição relativa de duas linhas por intervalos

Depois de vermos a teoria das posições relativas entre duas linhas por linhas, vamos ver como ela é colocada em prática através de um exemplo:

Encontre a posição relativa das duas linhas a seguir:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

As duas retas estão na forma de equações gerais (ou implícitas), portanto usaremos o método dos postos para encontrar a posição relativa entre as duas retas. Portanto, construímos a matriz A e a matriz estendida A’ com os coeficientes das retas:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Assim que tivermos as duas matrizes, precisamos calcular a classificação de cada uma. Primeiro calculamos a classificação da matriz A por determinantes:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

A matriz A contém o determinante de uma submatriz 3×3 diferente de zero, então a matriz A tem classificação 3 .

E agora calculamos o escopo da matriz estendida A’. A matriz A’ estará sempre pelo menos no posto da matriz A, que neste caso vale 3, portanto basta verificar se é de posto 4 ou de posto 3. Para isso, resolvemos o determinante da matriz 4× 4 por adições (ou cofatores):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

O determinante de toda a matriz estendida é zero, então a matriz A’ também é de posto 3 .

Portanto, a matriz A e a matriz A’ são de classificação 3 e, conseqüentemente, as duas retas se cruzam . Ou seja, existe apenas um ponto de intersecção entre eles.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Lembre-se que você tem acima uma tabela que resume todos os casos possíveis de posições relativas entre duas linhas de acordo com os contradomínios das matrizes A e A’.

Problemas resolvidos de posição relativa entre duas linhas no espaço

Exercício 1

Encontre a posição relativa entre as duas linhas a seguir:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

veja solução

Como ambas as retas são expressas como uma equação vetorial, encontraremos a posição relativa entre as duas retas a partir do método de um ponto e de um vetor de cada reta.

O vetor de direção de cada linha é:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

E um ponto que pertence a cada linha é:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Assim, para aplicar o procedimento, primeiro é necessário verificar se as componentes dos vetores de direção são proporcionais:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Como os dois vetores não são proporcionais entre si, as linhas só podem se cruzar ou se cruzar. Portanto, precisamos agora resolver o seguinte determinante que consiste no vetor diretor e um ponto em cada reta:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Substituímos os valores na fórmula:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

E calculamos o determinante:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

O resultado do determinante é equivalente a 0, então as linhas se cruzam .

Exercício 2

Calcule a posição relativa das duas linhas a seguir:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

veja solução

A primeira linha está na forma de equações paramétricas e a segunda linha está na forma de uma equação contínua, com a qual determinaremos a posição relativa entre as duas linhas a partir do método do vetor de um ponto de cada linha.

As coordenadas do vetor de direção da direita

$r$

são os coeficientes na frente do parâmetro

$t,$

e as coordenadas do vetor de direção da linha

$s$

são os números dos denominadores:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

E um ponto que pertence a cada linha é:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Assim, para aplicar o procedimento, primeiro é necessário verificar se as componentes dos vetores de direção são proporcionais:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

Os dois vetores são proporcionais entre si, portanto as retas só podem ser paralelas ou coincidentes. Para tirar essa dúvida, é necessário substituir o ponto na reta

$r$

na equação da reta

$s$

(ou vice-versa) para ver se satisfaz a referida equação:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Substituindo o ponto na reta obtemos uma igualdade, de modo que o ponto de uma reta satisfaz a equação da outra reta e, além disso, seus vetores diretores são proporcionais. Portanto, as duas linhas coincidem.

Exercício 3

Encontre a posição relativa das duas linhas a seguir:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

veja solução

As duas linhas estão na forma de equação geral (ou implícita), portanto usaremos o método de classificação para encontrar a posição relativa entre as duas linhas. Portanto, fazemos a matriz A e a matriz expandida A’ com os coeficientes das retas:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Assim que tivermos as duas matrizes, precisamos calcular a classificação de cada uma. Primeiro calculamos a classificação da matriz A por determinantes:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Todos os determinantes 3×3 da matriz A são zero, mas há um determinante 2×2 diferente de zero dentro da matriz, então a matriz A tem classificação 2 .

E agora calculamos o escopo da matriz estendida A’. A matriz A’ sempre será pelo menos o contradomínio da matriz A, que neste caso é 2, então é necessário verificar se ela possui um determinante 3×3 que não se anula e também quanto é o determinante do matriz inteira:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

A matriz estendida A’ de fato contém 3×3 subdeterminantes diferentes de zero e, além disso, o determinante de toda a matriz estendida é igual a 0, então a matriz A’ tem classificação 3 .

Portanto, a matriz A é de posto 2 e a matriz A’ é de posto 3, então as duas retas são paralelas . Ou seja, eles não têm nada em comum.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Lembre-se que na explicação do método (acima) você tem uma tabela que resume todos os casos possíveis de posições relativas entre duas linhas de acordo com os postos das matrizes A e A’.

Exercício 4

Encontre a posição relativa das duas linhas a seguir:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

veja solução

Neste caso, as duas retas estão na forma de equação cartesiana (ou implícita), então usaremos o método de ordenação para encontrar a posição relativa entre as duas retas. Portanto, construímos a matriz A e a matriz estendida A’ com os coeficientes das retas:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Depois de conhecermos as duas matrizes, precisamos calcular a classificação de cada uma. Calcularemos primeiro a classificação da matriz A por determinantes:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

A matriz A contém uma submatriz 3×3 cujo determinante é diferente de zero, então a matriz A tem classificação 3 .

E agora calculamos o escopo da matriz estendida A’. A matriz A’ será sempre pelo menos de posto da matriz A, que neste caso vale 3, então basta verificar se é de posto 4 ou de posto 3. Para isso, resolvemos o determinante de o conjunto da matriz 4×4 por adições (ou cofatores):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

O determinante de toda a matriz estendida é diferente de zero, então a matriz A’ tem classificação 4 .

Para que a matriz A seja de posto 3 e que pelo contrário a matriz A’ seja de posto 4, portanto as duas retas se cruzam em um ponto.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Lembre-se que na explicação do procedimento (acima) você tem uma tabela onde estão todos os casos possíveis de posições relativas entre duas linhas de acordo com os postos das matrizes A e A’.

Quais são as posições relativas de duas linhas no espaço?

Determinando a posição relativa de duas linhas de um ponto e um vetor

Exemplo de determinação da posição relativa entre duas linhas

Encontre a posição relativa de duas linhas por linhas

Exemplo de como encontrar a posição relativa de duas linhas por intervalos

Problemas resolvidos de posição relativa entre duas linhas no espaço

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta