Pontos de inflexão de uma função -

Aqui explicamos o que é um ponto de inflexão de uma função e como encontrar todos os pontos de inflexão de uma função. Além disso, você encontrará exercícios passo a passo sobre a curvatura e os pontos de inflexão de uma função.

Quais são os pontos de inflexão de uma função?

Os pontos de inflexão de uma função são os pontos nos quais o gráfico da função muda de curvatura, ou seja, em um ponto de inflexão uma função muda de côncava para convexa ou vice-versa.

Como saber se uma função tem um ponto de inflexão

Dada a definição de ponto de inflexão, vamos ver como saber se um determinado ponto é ponto de inflexão da função.

Uma função tem um ponto de inflexão em pontos que cancelam sua segunda derivada e sua terceira derivada é diferente de zero.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

Como exemplo, calcularemos os pontos de inflexão da seguinte função de terceiro grau:

$f(x)=x^3-5x$

Primeiro, calculamos a segunda e a terceira derivadas da função:

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

Agora definimos a segunda derivada igual a 0 e resolvemos a equação resultante:

$6x=0$

$x=0$

Então, o ponto x=0 será um ponto de inflexão da função se a terceira derivada for diferente de zero neste ponto. No nosso caso, a terceira derivada é sempre igual a 6.

$f'''(0)=6\neq 0$

Portanto, x=0 é um ponto de inflexão da função.

Como estudar a curvatura e encontrar os pontos de inflexão de uma função

Acabamos de ver um método para encontrar pontos de inflexão. Porém, normalmente tendemos a estudar a curvatura de uma função, ou seja, determinar a concavidade e a convexidade de uma função, e a partir daí calcular os pontos de inflexão.

Para encontrar os pontos de inflexão de uma função através de sua curvatura, devem ser executados os seguintes passos:

Encontre os pontos que não pertencem ao domínio da função.
Calcule a primeira derivada e a segunda derivada da função.
Encontre as raízes da segunda derivada , ou seja, calcule os pontos que cancelam a segunda derivada resolvendo
$f''(x)=0$

.
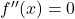
Faça intervalos com as raízes da derivada e os pontos que não pertencem ao domínio da função.
Calcule o valor da segunda derivada em um ponto de cada intervalo.
O sinal da segunda derivada determina a concavidade ou convexidade da função neste intervalo:
- Se a segunda derivada da função for positiva, a função é convexa neste intervalo.
- Se a segunda derivada da função for negativa, a função é côncava neste intervalo.
Os pontos de inflexão são os pontos nos quais a função muda de convexa para côncava ou vice-versa.

Para que você possa ver como os pontos de inflexão de uma função são calculados usando este procedimento, resolveremos um exemplo passo a passo abaixo:

Estude a curvatura e encontre os pontos de inflexão da seguinte função polinomial:

$f(x)=x^4-6x^2$

A primeira coisa a fazer é calcular o domínio de definição da função. É uma função polinomial, portanto o domínio da função consiste em números reais, ou seja, é uma função contínua:

$\text{Dom } f= \mathbb{R}$

Uma vez calculado o domínio da função, precisamos estudar em quais pontos ele é cumprido

$f''(x)=0$

Portanto, primeiro calculamos a primeira derivada da função:

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

A seguir, calculamos a segunda derivada da função:

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

E agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

Depois de calcularmos o domínio da função e

$f''(x)=0$

, representamos todos os pontos críticos encontrados na reta numérica:

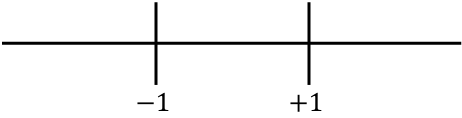
E agora avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Portanto, pegamos um ponto em cada intervalo (nunca os pontos críticos) e observamos qual sinal a segunda derivada tem neste ponto:

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Portanto, os intervalos de concavidade e convexidade da função são:

Convexo

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-1,1)}$

Além disso, em x=-1 a função vai de convexa para côncava, então x=-1 é um ponto de inflexão da função . E em x=1, a função vai de côncava para convexa, então x=1 também é um ponto de inflexão da função.

Finalmente, substituímos os pontos encontrados na função original para encontrar a coordenada Y dos pontos de inflexão:

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

Os pontos de viragem da função são, portanto:

Pontos de viragem:

$\bm{(-1,-5)}$

$\bm{(1,-5)}$

Abaixo você confere a representação gráfica da função estudada:

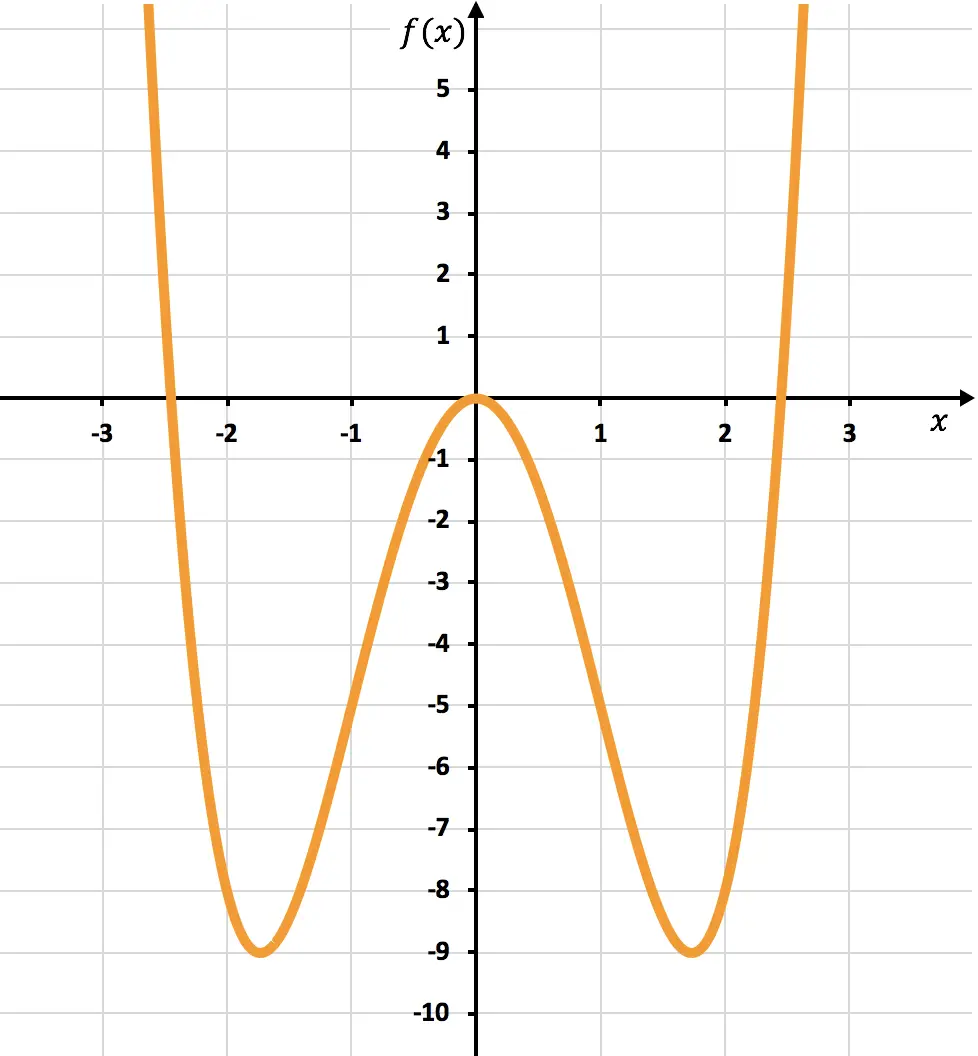
Como você pode ver no gráfico, a função vai de convexa

$(\cup)$

ser côncavo

$(\cap)$

Sobre

$(-1,-5)$

já que sua curvatura muda. E por outro lado, a função vai de côncava

$(\cap)$

ser convexo

$(\cup)$

Sobre

$(1,-5)$

Exercícios de giro resolvidos

Exercício 1

Calcule os intervalos de concavidade e convexidade, bem como os pontos de inflexão da seguinte função exponencial:

$f(x) = xe^x$

Veja a solução

A primeira coisa a fazer é calcular o domínio de definição da função. A função é composta por uma função polinomial (x), cujo domínio consiste apenas em números reais, e uma função exponencial ( ^ex ), cujo domínio também consiste em números reais. Portanto, o domínio da função consiste em números reais:

$\text{Dom } f= \mathbb{R}$

Agora vamos calcular a derivada da função. Neste caso, a função é composta pelo produto de duas funções, portanto para derivar a função precisamos aplicar a fórmula da derivada de um produto:

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

A seguir, calculamos a segunda derivada da função:

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

Definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)= 0$

$2e^x+xe^x= 0$

Extraímos o fator comum:

$e^x(2+x)=0$

Para que a multiplicação seja igual a 0, um dos dois elementos da multiplicação deve ser zero. Portanto, definimos cada fator igual a 0:

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

Um número elevado a outro nunca pode resultar em 0. Portanto, a equação

$e^x=0$

Não há solução.

Representamos todos os pontos singulares obtidos à direita:

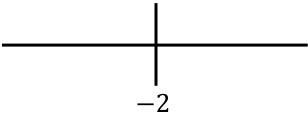
E agora avaliamos o sinal da segunda derivada em cada intervalo para saber se a função é côncava ou convexa. Para fazer isso, pegamos um ponto em cada intervalo e observamos qual sinal tem a segunda derivada nesse ponto:

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

Além disso, a função muda de côncava para convexa em x=-2, então x=-2 é um ponto de inflexão da função.

Finalmente, substituímos o ponto de inflexão encontrado na função original para encontrar a coordenada Y do ponto:

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

Concluindo, os únicos pontos de inflexão da função são:

Pontos de viragem:

$\bm{(-2,-2e^{-2})}$

Exercício 2

Estude os intervalos de concavidade e convexidade e encontre os pontos de inflexão da seguinte função racional:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Veja a solução

Primeiro precisamos calcular o domínio da função. Como se trata de uma função racional, igualamos o denominador a zero para ver quais números não pertencem ao domínio da função:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Isso significa que quando x for -2 ou +2, o denominador será 0. E portanto, a função não existirá. O domínio da função é, portanto, composto por todos os números, exceto x=-2 e x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Segundo, calculamos a primeira derivada da função:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

E então resolvemos a segunda derivada:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Todos os termos são multiplicados por

$(x^2-4)$

. Podemos, portanto, simplificar a fração:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Agora vamos calcular as raízes da segunda derivada da função:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

O termo

$\left(x^2-4\right)^3$

Isso envolve dividir todo o lado esquerdo, para que possamos multiplicá-lo por todo o lado direito:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Extraímos o fator comum:

$x(8x^2+96)=0$

Para que a multiplicação seja igual a 0, um dos dois elementos da multiplicação deve ser zero. Portanto, definimos cada fator igual a 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Não há solução, pois não existe raiz negativa de um número real.

Representamos agora na reta todos os pontos críticos obtidos, ou seja, os pontos que não pertencem ao domínio (x=-2 e x=+2) e aqueles que cancelam a segunda derivada (x=0):

E avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Então pegamos um ponto em cada intervalo e observamos qual sinal tem a segunda derivada nesse ponto:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

A função altera a curvatura em três pontos, portanto a função racional teria em princípio três pontos de inflexão, que são x=-2, x=0 e x=2. No entanto, embora haja uma mudança na curvatura em x=-2 e em x=+2, estes não são pontos de inflexão porque não pertencem ao domínio da função. Por outro lado, em x=0 há uma mudança na curvatura e isso pertence à função, então x=0 é o único ponto de inflexão da função.

Resta calcular a coordenada Y do ponto de inflexão:

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

Resumindo, o único ponto de inflexão da função racional é a origem das coordenadas:

Pontos de viragem:

$\bm{(0,0)}$

Exercício 3

Sabemos que a função

$f(x)=x^3+ax^2+bx+c$

passar pelo ponto

$(3,1)$

, tem um extremo relativo em

$x=1$

, e um ponto de viragem

$x = 2$

. A partir dessas informações, calcule os valores dos parâmetros

$a, b$

$c$

Veja a solução

Deixe a função ter um ponto de inflexão em

$x= 2$

significa que

$f''(2)=0$

. Portanto, calculamos a segunda derivada da função em

$x= 2$

e definimos como igual a 0:

$f(x) = x^3+ax^2+bx+c \ \longrightarrow \ f'(x)=3x^2+2ax+b$

$f'(x)=3x^2+2ax+b \ \longrightarrow \ f''(x)= 6x+2a$

$\left. \begin{array}{l} f''(2)=6\cdot 2+2a\\[2ex] f''(2)=0\end{array} \right\} \longrightarrow 6\cdot 2+2a=0$

E resolvemos a equação obtida para encontrar o valor do parâmetro a:

$6\cdot 2+2a=0$

$12+2a=0$

$2a=-12$

$a=\cfrac{-12}{2}$

$\bm{a=-6}$

A função será portanto:

$f(x)=x^3+ax^2+bx+c \ \xrightarrow{a \ = \ -6}\ f(x)=x^3-6x^2+bx+c$

Além disso, a função tem um extremo em

$x= 1$

, O que significa que

$f'(1)=0$

. Portanto, calculamos a primeira derivada da função em

$x= 1$

e definimos como igual a 0:

$f(x)=x^3-6x^2+bx+c \ \longrightarrow \ f'(x)=3x^2-12x+b$

$\left. \begin{array}{l} f'(1)=3\cdot 1^2-12\cdot 1+b\\[2ex] f'(1)=0\end{array} \right\} \longrightarrow 3\cdot 1^2-12\cdot 1+b=0$

E resolvemos a equação obtida para encontrar o valor da incógnita b:

$3\cdot 1^2-12\cdot 1+b=0$

$3 \cdot 1 -12 + b = 0$

$3 -12 + b = 0$

$b=+12-3$

$\bm{b=9}$

A função será portanto:

$f(x)=x^3-6x^2+bx+c \ \xrightarrow{b \ = \ 9} \ f(x)=x^3-6x^2+9x+c$

Por outro lado, dizem-nos que a função passa pelo ponto (3,1). Isso é para dizer,

$f(3)=1$

. Portanto, podemos aplicar esta condição para encontrar o valor do parâmetro c:

$\left. \begin{array}{l} f(3)=3^3-6\cdot 3^2+9\cdot3+c \\[2ex] f(3)=1 \end{array} \right\} \longrightarrow 3^3-6\cdot 3^2+9\cdot 3+c = 1$

E resolvemos a equação obtida para encontrar o valor de

$b:$

$3^3-6\cdot 3^2+9\cdot 3+c = 1$

$27-6\cdot 9+27+c = 1$

$27-54+27+c = 1$

$c=1-27+54-27$

$\bm{c=1}$

A função será portanto:

$f(x)=x^3-6x^2+9x+c \ \xrightarrow{c \ = \ 1} \ f(x)=x^3-6x^2+9x+1$

Quais são os pontos de inflexão de uma função?

Como saber se uma função tem um ponto de inflexão

Como estudar a curvatura e encontrar os pontos de inflexão de uma função

Exercícios de giro resolvidos

Exercício 1

Exercício 2

Exercício 3

Deixe um comentário Cancelar resposta