Como calcular os pontos de corte de uma função com os eixos

Esta página explica quais são os pontos de intersecção (ou cruzamento) de uma função com os eixos cartesianos e como calculá-los. Além disso, você encontrará diversos exemplos para entender completamente como eles são encontrados e poderá até praticar com exercícios resolvidos passo a passo.

Quais são os pontos de intersecção (ou intersecção) de uma função com os eixos?

Antes de ver como são calculados, vamos lembrar quais são os pontos de intersecção de uma função com os eixos.

Os pontos de interseção ou intersecção dos eixos são os pontos onde a representação de uma função intercepta os eixos coordenados, ou seja, os pontos do gráfico que se ligam ao eixo X e ao eixo l. Eixo Y.

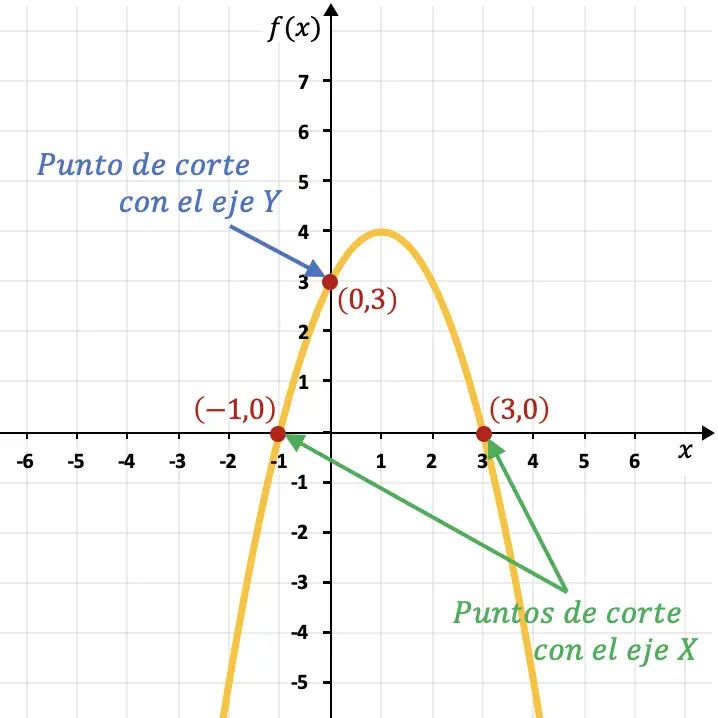
Por exemplo, a parábola no gráfico a seguir intercepta o eixo Y no ponto (0,3) e intercepta o eixo X nos pontos (-1,0) e (3,0).

Pontos de corte ou intersecção de uma função com os eixos

Ponto de corte de uma função com o eixo X

A segunda coordenada dos pontos de intersecção de uma função com o eixo X será sempre 0, portanto:

Os pontos de corte de qualquer função do eixo x OX são da forma

$(a,0)$

, e pode ser calculado resolvendo a seguinte equação:

$f(x)=0$

Às vezes, ao resolver esta equação podemos obter duas (ou mais) soluções, isso significa que a função intercepta o eixo X duas (ou mais) vezes. Por outro lado, se a equação não tiver solução, isso implica que a função não intercepta o eixo X.

Ponto de corte de uma função com o eixo Y

A primeira coordenada dos pontos de intersecção de uma função com o eixo Y será sempre 0, portanto:

O ponto de corte de qualquer função com o eixo y OY tem a forma

$(0,a)$

, e pode ser encontrado calculando a imagem da função em x=0:

$f(0)$

Ao contrário dos pontos de interrupção no eixo X, só pode haver um ponto de interrupção no eixo Y.

Exemplo de cálculo dos pontos de corte de uma função com os eixos

Para que você não tenha dúvidas, veremos a seguir um exemplo de como encontrar os pontos de corte de uma função com os eixos cartesianos:

Encontre numericamente os pontos de corte da seguinte função:

$f(x)=-2x+4$

Primeiro calcularemos o ponto de corte da função com o eixo x. O ponto de intersecção com o eixo X terá sempre a segunda componente igual a 0, ou seja, será do tipo

$(a,0)$

. Porque f(x) é sempre igual a 0 no eixo OX. Então, para encontrar a outra componente do ponto, precisamos resolver a equação

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

O ponto de intersecção com o eixo X é, portanto:

$\bm{(2,0)}$

Agora encontraremos o ponto de intersecção com o eixo y. O ponto de intersecção com o eixo Y sempre terá a primeira componente igual a 0, ou seja, o ponto será do tipo

$(0,a)$

. Já que a variável independente x sempre se cancela no eixo Y. Então, para encontrar a outra coordenada do ponto, precisamos calcular

$f(0):$

$f(0)=-2 \cdot 0+4=4$

O ponto de intersecção com o eixo Y é, portanto:

$\bm{(0,4)}$

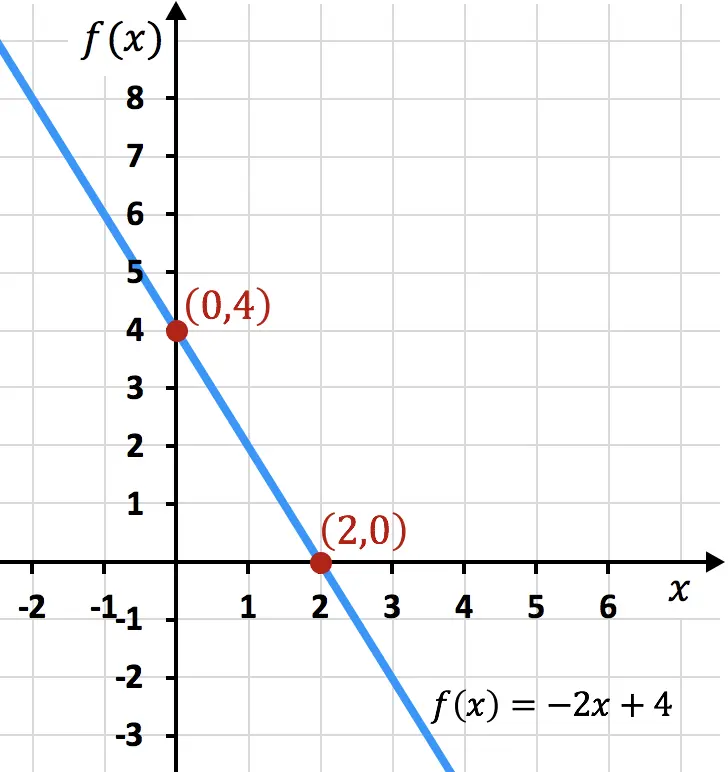
Abaixo você tem a função de exemplo representada graficamente, você pode ver que os limites encontrados coincidem com os do gráfico:

como encontrar os pontos de corte de uma função com eixos

Exercícios resolvidos para pontos de corte de uma função com eixos

Exercício 1

Determine os pontos de corte com os eixos coordenados da seguinte função:

$f(x)=3x-3$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto de intersecção da função com o eixo X é necessário resolver

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

O ponto de intersecção da função com o eixo X é, portanto:

$\bm{(1,0)}$

Ponto de corte com eixo Y

Para encontrar o ponto de intersecção com o eixo Y você deve calcular

$f(0):$

$f(0)=3\cdot 0 -3= -3$

O ponto de intersecção da função com o eixo Y é, portanto:

$\bm{(0,-3)}$

Exercício 2

Encontre os pontos de intersecção com os eixos cartesianos da seguinte função afim:

$f(x)=2x+8$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto limite da função com o eixo OX, precisamos igualar a função a zero e resolver a equação resultante:

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

Portanto, o ponto de intersecção da função com o eixo das abcissas é:

$\bm{(-4,0)}$

Ponto de corte com eixo Y

Para encontrar o ponto de corte com o eixo OY, precisamos calcular

$f(0):$

$f(0)=2\cdot 0 +8= 8$

O ponto de intersecção da função com o eixo do computador é, portanto:

$\bm{(0,8)}$

Exercício 3

Calcule os pontos de corte com os eixos da seguinte função quadrática:

$f(x)=x^2-3x+2$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto de intersecção da função com o eixo X é necessário resolver

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

Neste caso, precisamos resolver uma equação quadrática, então aplicamos a fórmula:

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

Obtivemos duas soluções da equação quadrática, então a função intercepta o eixo X em dois pontos:

$\bm{(1,0)} \qquad \bm{(2,0)}$

Ponto de corte com eixo Y

Por outro lado, para determinar o ponto de intersecção com o eixo Y, é necessário calcular

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

Portanto, o único ponto de intersecção da função com o eixo Y é:

$\bm{(0,2)}$

Exercício 4

Encontre os pontos de intersecção com os eixos do plano cartesiano da seguinte função racional:

$f(x)=\cfrac{5}{x}$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto de intersecção da função com o eixo X é necessário resolver

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5 não é equivalente a 0, portanto a equação não tem solução e, portanto, não há ponto de intersecção entre a função e o eixo X.

Ponto de corte com eixo Y

Para encontrar o ponto de intersecção com o eixo Y você deve calcular

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

Qualquer número dividido por zero é uma indeterminação que dá infinito. Portanto, a função não se estende além do eixo Y em nenhum ponto.

Resumindo, a função exercício não possui pontos de intersecção com os eixos , ou seja, seu gráfico não passa pelo eixo X nem pelo eixo Y em nenhum ponto.

Exercício 5

Calcule os pontos de corte com os eixos da seguinte função de terceiro grau:

$f(x)=x^3-9x$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto de intersecção da função com o eixo X é necessário resolver

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

Ambos os termos da equação possuem um x , com o qual podemos extrair um fator comum:

$x(x^2-9)=0$

Para que a igualdade anterior seja satisfeita, um dos fatores deve ser 0. Portanto, igualamos cada fator a zero para obter todas as soluções possíveis:

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

Obtivemos, portanto, três soluções da equação do terceiro grau, portanto a função corta o eixo X em 3 pontos:

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

Ponto de corte com eixo Y

Para calcular o ponto de corte com o eixo Y, é necessário calcular

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

Portanto, o único ponto de intersecção da função com o eixo Y é a origem da coordenada (0,0):

$\bm{(0,0)}$

Observe que já havíamos encontrado este ponto no cálculo do ponto de corte com o eixo X, pois a função corta neste ponto com os dois eixos ao mesmo tempo.

Pontos de corte ou interseção de uma função com os eixos

Quais são os pontos de intersecção (ou intersecção) de uma função com os eixos?

Ponto de corte de uma função com o eixo X

Ponto de corte de uma função com o eixo Y

Exemplo de cálculo dos pontos de corte de uma função com os eixos

Exercícios resolvidos para pontos de corte de uma função com eixos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta