Polinomial

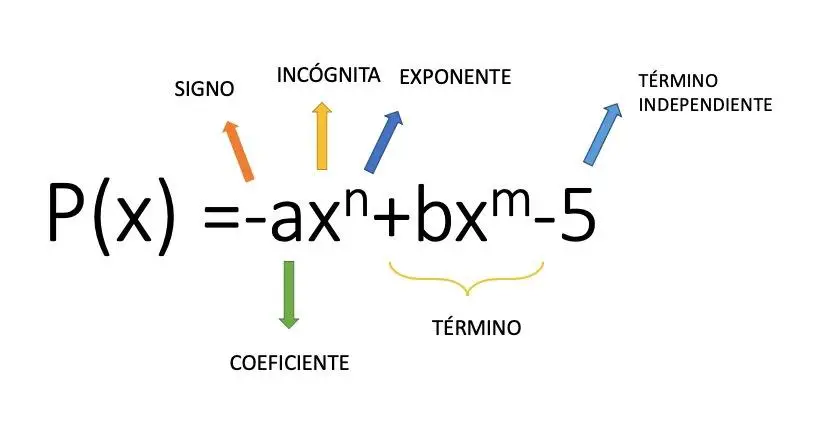
Um monômio é uma expressão algébrica formada por um coeficiente (valor numérico) que multiplica uma variável por um expoente, por exemplo a expressão 4x² é um monômio. Então a partir deste conceito matemático chegamos ao polinômio que é um conjunto de adições e subtrações de vários monômios. Na imagem acima você pode ver um exemplo da estrutura de um polinômio composto por vários monômios.

tipos de polinômios

Através do expoente de um determinado monômio, podemos classificar os polinômios em diferentes tipos. Podemos classificar essas expressões em categorias como: polinômio de primeiro grau, polinômio de segundo grau, polinômio de terceiro grau, etc. Basicamente, você precisa identificar o monômio que possui o maior expoente e qual será o grau do polinômio . E depois de saber disso, você pode classificá-lo em um dos tipos de que acabamos de falar.

Polinômio de diversas variáveis

Além disso, existe também outra forma de organizar polinômios, que é de acordo com o número de monômios que os formam. Por exemplo, se tivermos um binômio , isso será equivalente a ter um polinômio com dois termos, se tivermos um trinômio , isso será equivalente a ter um polinômio com três termos, etc. Todas essas formas de catalogar polinômios têm infinitas subcategorias. Visto que estas expressões podem ser compostas por quaisquer monômios que quisermos e também podem ter qualquer grau.

Características e propriedades de polinômios

• Grau absoluto de um polinômio: Na seção anterior, discutimos a definição de grau relativo. Mas no caso de polinômios formados por mais de uma variável, temos o grau absoluto que equivale à soma máxima dos expoentes de todas as variáveis deste monômio. Por exemplo, no monômio 5x²y³, o grau absoluto é igual a 2 + 3 = 5.
• Polinômio ordenado: Definimos um polinômio ordenado em relação a uma variável quando os expoentes dessa variável estão organizados em ordem crescente ou decrescente. Por exemplo, se encontrarmos este polinômio P(x) = 3x + 4x³ – x², neste caso ele não estará ordenado. Então, deveríamos corrigi-lo e obteríamos este resultado: P(x) = 4x³ – x² + 3x.
• Polinômio completo: Quando encontramos um polinômio que possui monômios com todos os expoentes possíveis (do maior grau ao termo independente), dizemos que é um polinômio completo . Por exemplo, a seguinte expressão: P(x) = 3 x² + 2x – 4 é deste tipo porque não há expoente faltante entre 2 e 0.
• Polinômio homogêneo: é aquele polinômio que possui grau absoluto igual em cada um de seus monômios. As variáveis podem ter valores diferentes no expoente, mas a soma dos expoentes das variáveis em todos os monômios deve ser necessariamente a mesma. Por exemplo: P(x) = x²y³z + 3 x ⁴ yz, as duas somas dão seis 2 + 3 + 1 = 4 + 1 + 1 = 6.
• Polinômios idênticos: Quando encontramos dois ou mais polinômios que compartilham os coeficientes dos mesmos termos, diremos que são polinômios idênticos. Abaixo você pode ver um exemplo entre dois polinômios: P(x) = 2x + 27 e Q(x) = 5 (x + 3) – 3 (x – 4), eles serão idênticos porque compartilham os coeficientes de cada expoente : 2x = 5x – 3x e 27 = 15 + 12.
• Polinômio zero: Este polinômio possui apenas coeficientes zero (iguais a zero), portanto o valor total do polinômio também será zero. O polinômio P(x) = 0x³ + 0x² – 0x – 0 é um exemplo claro desse tipo de polinômio, mas não deve ser confundido com Q(x) = 0, pois neste caso você forma uma equação e ela não não significa que todos os coeficientes de Q(x) sejam 0.

Valor numérico de um polinômio

O valor numérico de um polinômio é o resultado que obteremos substituindo a variável desta expressão por um número. Precisamos simplesmente resolver este polinômio como se fosse uma operação combinada . A seguir, explicaremos os três métodos que você pode usar para obter o valor numérico de uma expressão como esta.

• Substituição direta: quando nos são dados diretamente os valores correspondentes a cada uma das variáveis do polinômio, simplesmente substituímos essas variáveis por esses números. Desta forma, se tivermos o polinômio P(x) = 2x² – x + 4 e nos for dito que x = 3, então o valor numérico do polinômio será igual a 2 · 3² – 3 + 4 = 19.
• Resolução de variáveis: aplicaremos este caso quando não nos derem diretamente o valor da variável, mas nos derem uma equivalência. Por exemplo, P(2) se P(x – 1) = x³ – 2x + 1 for verdadeiro, então primeiro resolveremos a equação 2 = x – 1 e obteremos x = 3. Finalmente, teremos que substituir 3 para x, tal que 3³ – 2 · 3 + 1 = 22.
• Mudança de variável: quando temos um polinômio P(x) = 4x – 2 e queremos saber esse valor para P(x + 2). A seguir, precisamos alterar todos os x na expressão para a(x+2). Dito isso, vamos ver como ficaria este último exemplo resolvido: P(x + 2) = 4 (x + 2) – 2.

Operações com polinômios

A seguir explicaremos como resolver as quatro operações aritméticas básicas com polinômios , sempre seguindo a hierarquia das operações . Em cada seção você encontrará um pouco de teoria que lhe permitirá saber como proceder em cada caso e alguns exemplos práticos.

adição de polinômios

Para adicionar polinômios devemos levar em consideração o fato de que eles só podem ser agrupados por termos semelhantes , portanto se tivermos os polinômios P(x) = 3x³ – x² + 2x – 4 e Q(x) = 2x² + 3x – 2. Então para fazer P(x) + Q(x), vamos somar os coeficientes dos dois polinômios acompanhados do mesmo expoente: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Resumindo, podemos dizer que agrupamos e somamos os coeficientes de cada termo semelhante e no final expressamos todos os termos em um único polinômio .

subtração de polinômios

A subtração de polinômios é resolvida da mesma forma que a adição, a única diferença é obviamente o símbolo. Depois agrupamos termos semelhantes, subtraímos e transformamos tudo em uma única expressão. Abaixo mostraremos usando um exemplo: P(x) = 5x³ – 2x² + x – 3 e Q(x) = 3x² + 5x + 4, então P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

multiplicação polinomial

Na hora de resolver esse tipo de multiplicação as coisas podem ficar um pouco complicadas, mas se você seguir todos os passos que vamos te contar, você ficará bem. Nesta operação matemática todos os monômios irão operar com todos os outros, isso significa que não iremos apenas multiplicar termos semelhantes. Além disso, não apenas os coeficientes mudarão , mas os expoentes também mudarão . Com este exemplo você entenderá tudo muito melhor: P(x) = 2x² + 3x – 1 e Q(x) = 2x + 3:

P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

Basicamente, multiplicamos os coeficientes de cada termo de um polinômio por todos os do segundo e depois aplicamos a propriedade de potência de a ⁿ · a ^m = a ^n+m .

divisão de polinômios

Por fim, só precisamos explicar como resolver a divisão de polinômios, basicamente precisamos aplicar a propriedade distributiva da divisão: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷d). E também aplicaremos a seguinte propriedade de exponenciação a ⁿ ÷ a ^m = a ^nm . Veremos isso agora com um exemplo simples: P(x) = 3x³ – 6x² + 9x e Q(x) = 3x.

P(x) ÷ Q(x) = ( 3x³ – 6x² +9x )÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3

Agora que você terminou de ver como resolver todas essas operações com polinômios, esperamos que saiba como aplicá-las na prática. Mas se você acha que não é esse o caso e quer continuar praticando um pouco, recomendamos que dê uma olhada em alguns exercícios resolvidos nesta página . Isso o ajudará a terminar de internalizar todos esses conceitos matemáticos.

Fatoração de polinômios

Para fatorar polinômios, você pode fazê-lo manualmente conforme explicado no artigo deste último link ou pode fazê-lo usando uma calculadora Ruffini . Recomendamos fazer isso com esta segunda opção se quiser fazer isso rapidamente, mas se você está apenas aprendendo a fatorar, é melhor praticar manualmente. A maneira de fazer isso deve ser escolhida com base na sua situação.

Resolva polinômios com a calculadora científica

Existem muitas calculadoras científicas diferentes no mercado hoje. Mas se você está procurando uma calculadora barata que possa resolver polinômios , recomendamos a Casio FX-991SPX II . É fácil de usar, muito poderoso e funcional, tornando-o perfeito para qualquer estudante de matemática do ensino fundamental e médio. A seguir explicaremos brevemente como as expressões matemáticas deste estilo são resolvidas usando este ou um modelo semelhante da Casio.

Você deve primeiro inserir o valor numérico das variáveis, escrevê-lo e pressionar “STO” + letra da variável , por exemplo x. Então, quando todas as variáveis estiverem definidas, você só precisa escrever a expressão polinomial como está com todas as variáveis e todos os números. E por último deve-se pressionar a tecla igual, assim obterá o resultado equivalente ao valor numérico do polinômio.