Planos perpendiculares

Nesta página você encontrará o que são planos perpendiculares, como determinar se dois planos são perpendiculares, como calcular um plano perpendicular, exemplos e exercícios resolvidos de planos perpendiculares,…

O que são dois planos perpendiculares?

Na geometria analítica, dois planos são perpendiculares quando se cruzam em ângulos retos (90º).

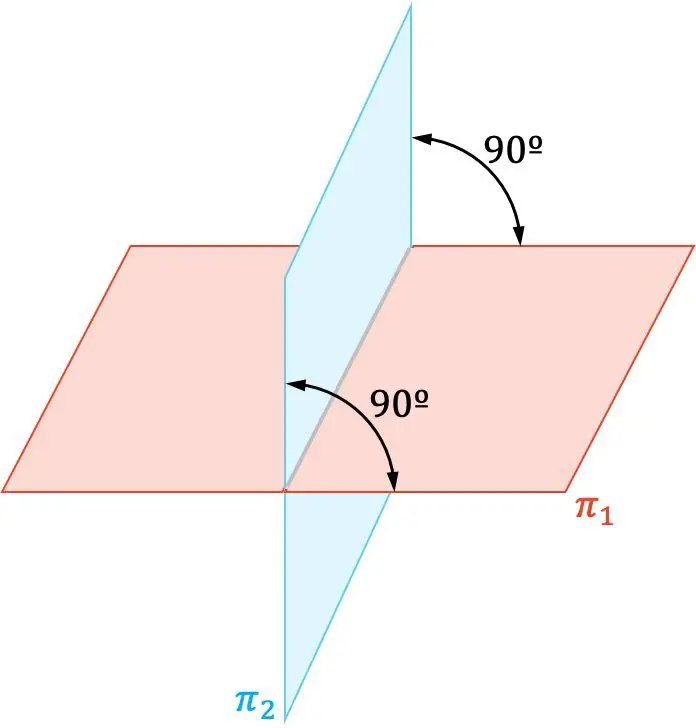
Além disso, os vetores normais de dois planos perpendiculares também são ortogonais entre si.

Obviamente, a distância entre dois planos perpendiculares é sempre zero, porque eles se cruzam numa linha. Embora pareça muito simples, o conceito de distância entre dois planos é muito importante, por isso recomendamos visitar o link caso tenha alguma dúvida sobre o assunto.

Por outro lado, dois planos posicionados perpendicularmente não são a única posição relativa possível entre planos, uma vez que dois planos no espaço (em R3) também podem ser cruzados, paralelos ou coincidentes.

Como você sabe se um plano é perpendicular a outro?

Depois de vermos a definição de planos perpendiculares, vamos ver como saber se dois planos são perpendiculares ou não:

Dois planos são perpendiculares quando seus vetores normais são perpendiculares. Portanto, para determinar se dois planos são perpendiculares entre si, devemos calcular o ângulo formado pelos seus vetores normais, e se estes formam um ângulo de 90º, isso significa que os planos são perpendiculares.

Então, para encontrar a perpendicularidade de dois planos você precisa saber como calcular o ângulo entre dois vetores . Se não se lembra como fazer, pode consultar o link, onde encontrará a nossa explicação bem como a fórmula necessária para determinar o ângulo entre dois vetores. Além disso, você poderá ver exemplos e praticar com exercícios resolvidos.

Mas, resumindo, dois vetores são perpendiculares quando seu produto escalar é zero. Portanto, dois planos serão perpendiculares quando o produto escalar de seus vetores normais associados for 0.

Exemplo de dois planos perpendiculares

Por exemplo, vamos verificar se os dois planos a seguir são perpendiculares:

$\pi_1 : \ 3x-4y+2z+5 =0$

$\pi_2 : \ 2x+5y+7z-6 =0$

As coordenadas X, Y, Z do vetor normal a um plano coincidem com os coeficientes A, B, C de sua equação geral (ou implícita). Portanto, o vetor normal a cada plano é:

$\vv{n}_1 =(3,-4,2)$

$\vv{n}_2 =(2,5,7)$

E agora verificamos se estes são dois planos perpendiculares calculando o produto escalar entre seus vetores normais:

$\begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}$

O produto escalar entre os dois vetores normais é 0, então os dois planos são perpendiculares entre si.

Calcular um plano perpendicular a uma reta em um ponto

Um problema típico de planos e retas é encontrar a equação de um plano perpendicular a uma reta em um determinado ponto. Então, a seguir veremos como isso se resolve por meio de um exemplo:

Encontre a equação do plano perpendicular à linha.
$r$

Sobre

$P,$

sendo dito direto e ponto:

$\displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)$

Primeiro, precisamos determinar o vetor normal ao plano em questão. e como a linha reta

$r$

é perpendicular ao plano, seu vetor normal coincidirá com o vetor de direção da reta.

Neste caso, a linha

$r$

está na forma de equações paramétricas, então os componentes de seu vetor de direção são os termos na frente do parâmetro

$t:$

$\vv{r} =(-2,4,1)$

Assim, o vetor normal ao plano será igual ao vetor de direção da reta:

$\vv{n} =(-2,4,1)$

E, portanto, a equação implícita (ou geral) do plano será a seguinte:

$\pi : \ -2x+4y+1z+D=0$

É, portanto, suficiente determinar o valor do coeficiente D. Para isso, substituímos na sua equação as coordenadas do ponto cuja afirmação nos diz que pertence ao plano:

$P(1,3,-2)$

$-2\cdot 1+4\cdot 3-2+D=0$

$-2+12-2+D=0$

$8+D=0$

$D=-8$

Resumindo, a equação cartesiana do plano é:

$\bm{\pi : \ -2x+4y+z-8=0}$

Por outro lado, se quiser praticar mais exercícios de perpendicularidade entre objetos geométricos, pode visitar nossa página sobre retas perpendiculares. Você encontrará tudo o que precisa saber sobre retas perpendiculares : quando duas retas são perpendiculares, como calcular uma perpendicular à outra, exemplos, exercícios resolvidos e muito mais.

Propriedades de planos perpendiculares

Todos os planos perpendiculares possuem as seguintes características:

Relação simétrica : Se um plano é perpendicular a outro plano, este plano também é perpendicular ao primeiro plano. Esta propriedade também é mantida por planos paralelos.

$\pi_1 \bm{\perp} \pi_2 \ \longrightarrow \ \pi_2 \bm{\perp} \pi_1$

Propriedade não reflexiva : Obviamente, nenhum plano pode ser perpendicular a si mesmo.

$\pi_1 \ \cancel{\bm{\perp}}} \ \pi_1$

Teorema: No espaço tridimensional (3D), qualquer par de planos perpendiculares a um terceiro plano deve ser necessariamente paralelo. Em outras palavras, se um plano é perpendicular a outro plano e este plano também é perpendicular a um terceiro plano, o primeiro e o último planos são paralelos entre si.

O que são dois planos perpendiculares?

Como você sabe se um plano é perpendicular a outro?

Exemplo de dois planos perpendiculares

Calcular um plano perpendicular a uma reta em um ponto

Propriedades de planos perpendiculares

Deixe um comentário Cancelar resposta