Planos paralelos - Mathority

Nesta página você encontrará tudo sobre planos paralelos: quando dois planos são paralelos, as equações de dois planos paralelos, exemplos, exercícios resolvidos, propriedades,…

O que são dois planos paralelos?

Na geometria analítica, dois planos são paralelos quando estão sempre à mesma distância. Portanto, dois planos paralelos nunca se cruzam e não têm nada em comum.

Dois planos posicionados paralelamente não são a única posição relativa possível entre planos, uma vez que dois planos no espaço (em R3) também podem se cruzar ou coincidir.

Como você sabe se dois planos são paralelos?

Depois de ver a definição de planos paralelos, vamos ver como determinar se dois planos são paralelos ou não.

Partindo da equação geral (ou implícita) de dois planos diferentes:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

Os 2 planos serão paralelos se os seus coeficientes A, B e C forem proporcionais entre si e não ao coeficiente D. Em outras palavras, o paralelismo entre dois planos ocorre quando a seguinte equação é satisfeita:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Exemplo de dois planos paralelos

Por exemplo, os dois planos a seguir são paralelos:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

Os planos são paralelos porque os coeficientes das variáveis X, Y, Z são proporcionais entre si, mas não aos termos independentes:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Calcule a distância entre dois planos paralelos

Dois planos paralelos estão sempre à mesma distância, portanto, para determinar a distância entre dois planos paralelos, podemos pegar num ponto num dos dois planos e calcular a distância desse ponto ao outro plano. Portanto, para calcular a distância entre 2 planos paralelos, é necessário conhecer a fórmula da distância de um ponto a um plano .

É um método para encontrar a distância entre dois planos paralelos. Porém, existe uma maneira ainda mais simples de fazer isso quando os coeficientes A, B e C das equações dos dois planos coincidem:

Considere as equações gerais (ou implícitas) de dois planos paralelos:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

A fórmula para calcular a distância entre dois planos paralelos é:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

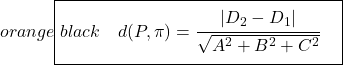
Então com certeza é mais fácil encontrar a distância entre dois planos paralelos usando a fórmula, pois é só aplicar a fórmula e pronto, mas depende do problema. Além disso, achamos melhor explicar as duas formas de calcular a distância para que você possa escolher a que preferir.

Exemplo de cálculo da distância entre dois planos paralelos

Como exemplo, calcularemos a distância entre os dois planos a seguir:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Devemos primeiro verificar se estamos lidando com dois planos paralelos. Assim, todos os coeficientes das equações planas são proporcionais, exceto os termos independentes, portanto são efetivamente dois planos paralelos.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Neste caso, os termos A, B e C das equações dos dois planos não coincidem, mas podemos conseguir isso dividindo toda a equação do segundo plano por dois:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Assim, as equações dos dois planos passam a ter os mesmos coeficientes A, B e C. Portanto, podemos calcular facilmente a distância entre os dois planos com a fórmula da distância entre dois planos paralelos:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Substituímos os valores e resolvemos as operações:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Para que a distância entre um plano e outro plano seja igual à unidade.

Propriedades de planos paralelos

As características dos planos paralelos são as seguintes:

Propriedade reflexiva : Cada plano é paralelo a si mesmo.

$\pi_1 \parallel \pi_1$

Propriedade simétrica : Se um plano é paralelo a outro, este plano também é paralelo ao primeiro. Esta propriedade também é possuída por planos perpendiculares.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Propriedade transitiva : se um plano é paralelo a outro plano, e este segundo plano é paralelo a um terceiro plano, o primeiro plano também é paralelo ao terceiro plano.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$