Os números complexos são um conjunto composto por números reais e números imaginários . Esses dois últimos conjuntos numéricos podem ser representados graficamente usando a reta real e a reta imaginária. E quando colocamos ambas as retas no mesmo plano, forma-se o conhecido plano complexo.
Qual é o plano complexo?
O plano complexo é formado pelo eixo real (eixo X), que equivale à reta real e, por outro lado, pelo eixo imaginário (eixo Y), que conceitua a reta imaginária.
Deve-se notar que este plano inclui todos os números complexos. Portanto, não importa quão pequeno ou pequeno seja, ou em que forma um número complexo esteja escrito, ele pode ser representado graficamente no plano. Então vamos ver como esses números são representados no plano complexo.
Como representar graficamente números complexos no plano complexo?
Como já sabemos (ou se não sabe, aconselhamos a leitura do nosso artigo sobre números complexos ), existem três formas de escrever um complexo: a forma binomial, a forma polar e a forma trigonométrica. Cada um expressa o valor complexo de acordo com uma estrutura diferente, portanto o método a seguir para fazer as representações gráficas é diferente.
A seguir explicamos o procedimento a seguir nos três casos:
Representação em forma binomial
Quando temos um número complexo em notação binomial , que é a mais comum, devemos observar a estrutura do número:

onde a é a parte real e b é a parte imaginária.
Sabendo disso, deduzimos que o valor de a é o que utilizamos para a abcissa (eixo real) e o valor de b é o que utilizamos para o computador (eixo imaginário). Com o exemplo a seguir você entenderá melhor.
Tentaremos representar o número: 3 + 2i.
A primeira coisa é desenhar o gráfico (observando que o eixo horizontal é o real e o eixo vertical é o imaginário):

A seguir, localizamos o ponto do gráfico nas coordenadas cartesianas (x, y), que deduzimos do número complexo. Neste exemplo prático, nosso ponto é (3, 2).
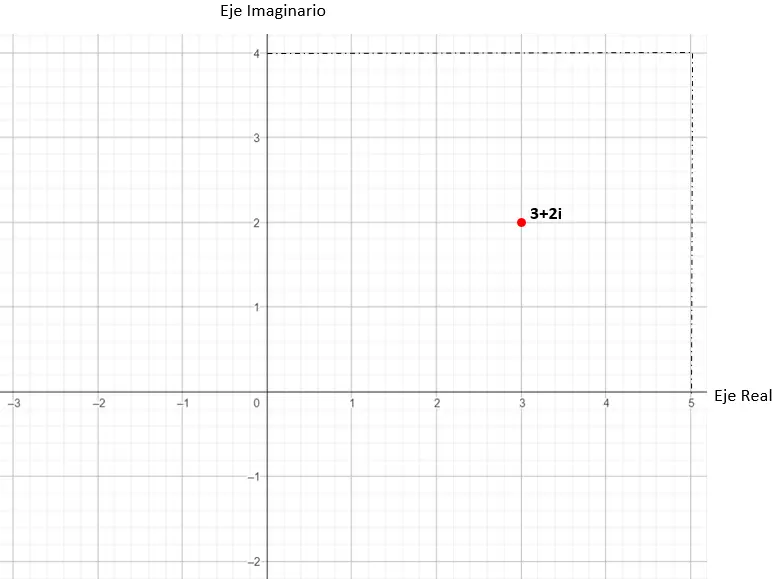
Assim o valor 3 + 2i seria representado no plano complexo.
Representação em forma polar
Veremos agora como um número complexo é representado na forma polar . Para compreender totalmente este método, você precisa saber que a notação polar define um número complexo com base no módulo e no argumento. Que são utilizadas na representação gráfica como coordenadas polares (e não como coordenadas cartesianas!).
E a principal característica do sistema de coordenadas polares é que a localização de um ponto é descrita por meio de um vetor e um ângulo (não como no método anterior). Que corresponde ao módulo e ao argumento dos números complexos. A seguir, mostramos a fórmula universal para a forma polar de um número complexo:

Onde |z| é o módulo e α é o argumento. Estas duas variáveis são traduzidas no plano por:
- Módulo: é o comprimento que define um vetor (entre a origem e o ponto equivalente ao nosso número).
- Argumento: é o ângulo que o vetor faz com o eixo X.
Portanto, o módulo de um número complexo corresponde ao comprimento do vetor que utilizamos para fazer o gráfico. Enquanto o argumento ou ângulo do número complexo é o ângulo entre o vetor e o eixo X. Abaixo você pode ver um diagrama que coloca todas as variáveis :
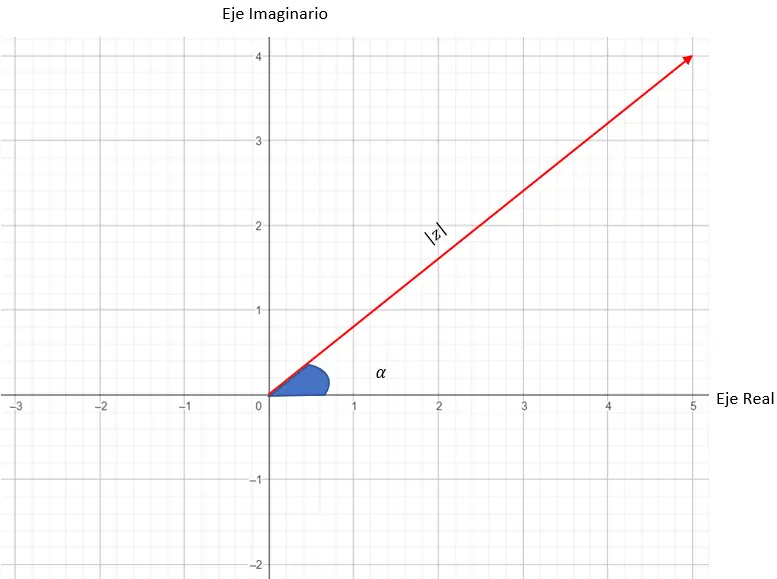
Agora tentaremos representar o número: 3 45 .
Primeiro, precisamos identificar o módulo e o argumento:
- Módulo: 3.
- Argumento: 45 graus.
A seguir precisamos encontrar os pontos do gráfico que possuem módulo igual a 3, neste caso qualquer ponto de um círculo de raio 3 funcionará.
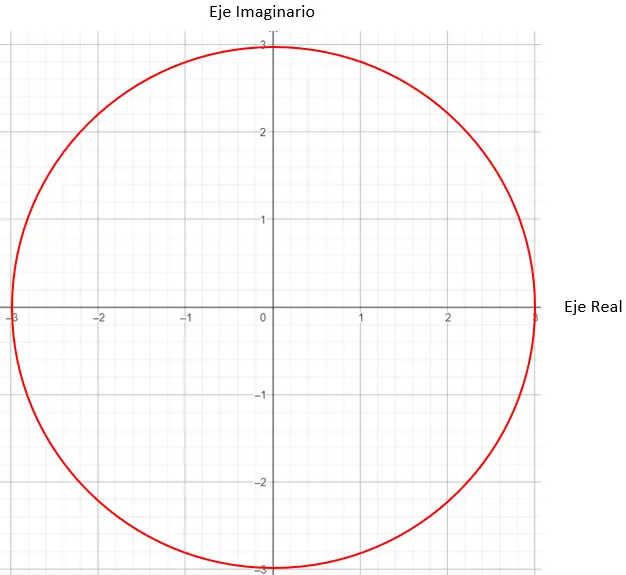
E para finalizar a determinação de qual é o ponto exato, devemos colocar a condição de que o vetor gerado pelo módulo e a origem façam um ângulo de 45 graus com o eixo X.
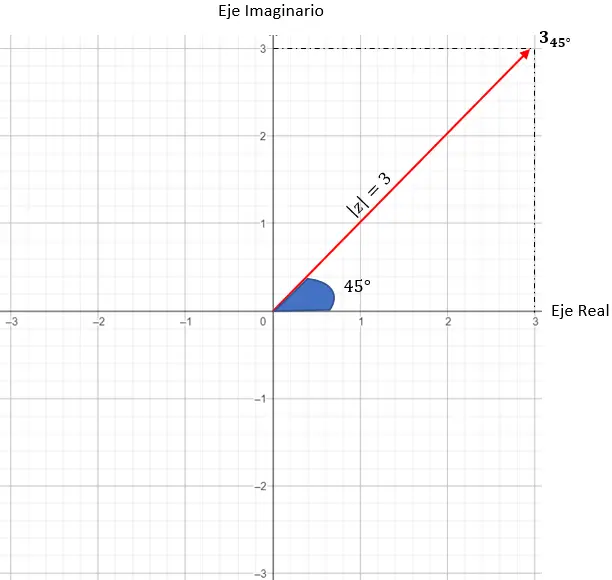
E já temos um número complexo representado em notação polar.
Representação em forma trigonométrica
Por fim, ainda temos que explicar como um número complexo é representado na forma trigonométrica . Este caso e o anterior são praticamente iguais, pois a forma polar e a forma trigonométrica utilizam os mesmos dados para expressar um número complexo: o módulo e o argumento. Isso apenas altera a estrutura da expressão:

Onde, |z| é o módulo e α é o argumento.
Devemos, portanto, aproveitar o mesmo método do caso anterior: usar o módulo como “comprimento” e o argumento como ângulo. Ao ver o exemplo a seguir, você entenderá melhor.
Representaremos z = 4 · (cos (45) + i · sin(45)).
A primeira coisa é identificar o módulo e o ângulo:
- Módulo: 4.
- Argumento: 45 graus.
A seguir, precisamos encontrar os pontos do gráfico que possuem módulo igual a 4, neste caso qualquer ponto de um círculo de raio 4 funcionará.
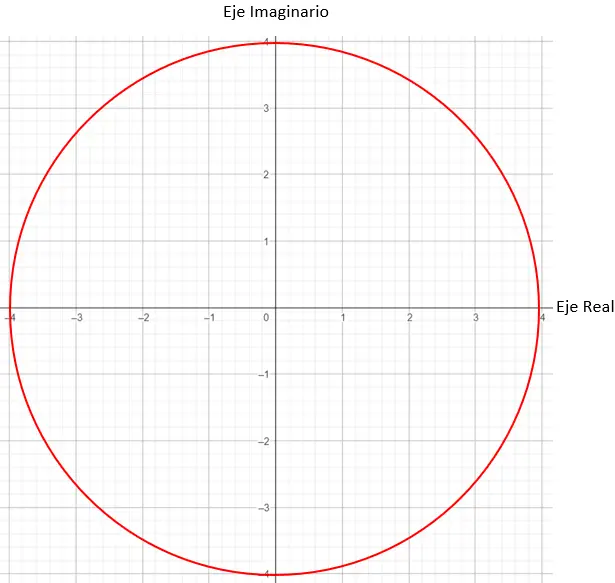
E por fim, localizamos o ponto exato, exigindo que o ângulo formado entre o vetor módulo e o eixo X seja de 45 graus, como nos diz o argumento.
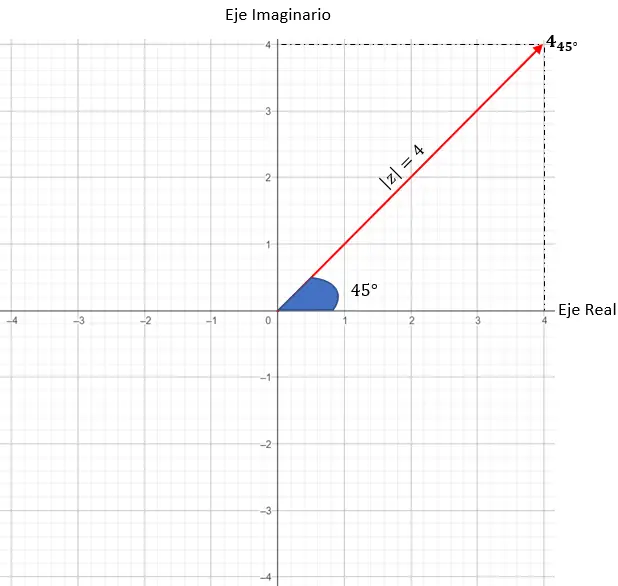
E assim representamos um número complexo na forma trigonométrica.
Exercício complexo de avião
Para finalizar esta publicação, vamos oferecer um último exercício. Recomendamos fortemente que você resolva, pois assim você consolidará os conhecimentos explicados ao longo deste artigo.
Prova da representação gráfica dos seguintes três números complexos no plano complexo:
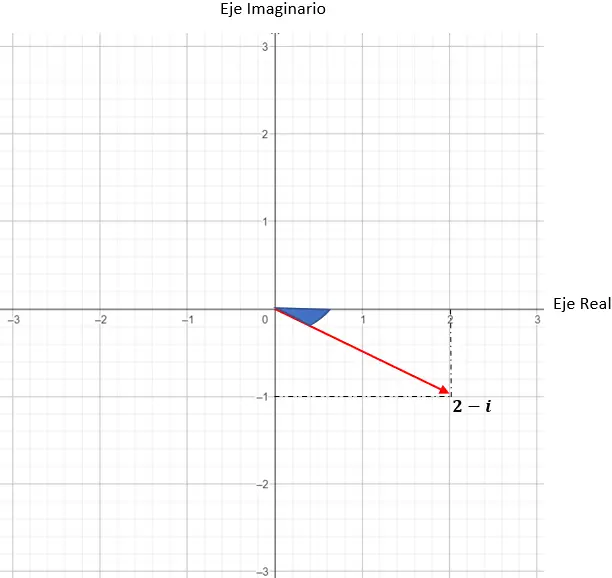
z = 2 – eu
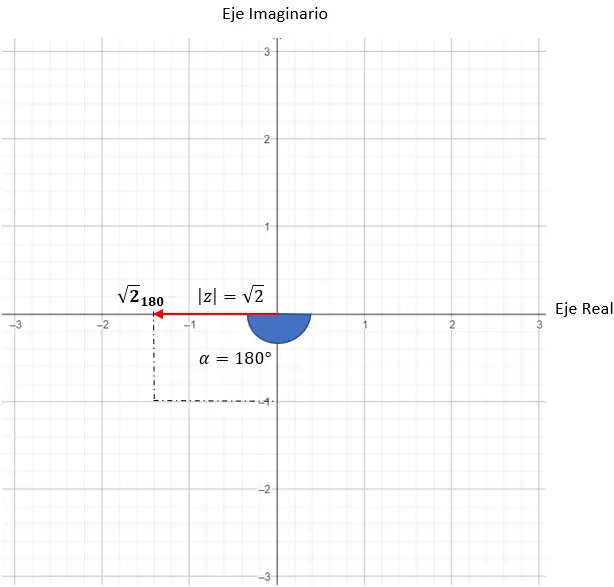
w = √2180
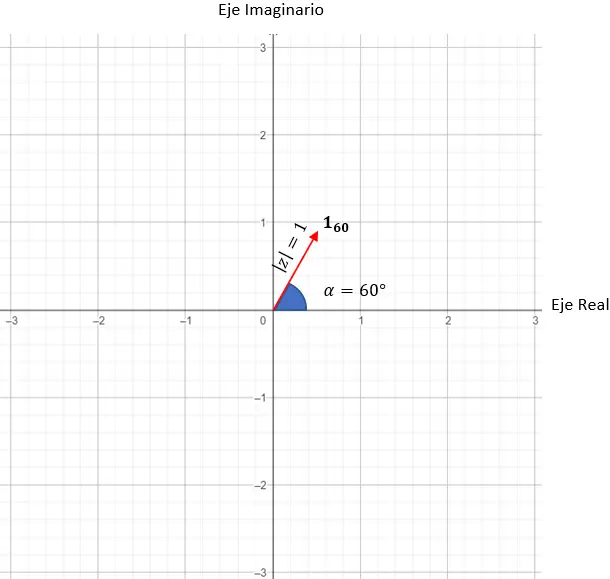
p = cos(60) + eu sin(60)