Neste artigo explicamos o que é a periodicidade de uma função. Além disso, você verá vários exemplos de funções periódicas. Por fim, analisaremos o período das funções trigonométricas, pois é uma de suas características mais importantes.
Qual é a periodicidade de uma função?
A periodicidade de uma função é uma característica de funções que repetem seus valores ciclicamente, ou seja, uma função é periódica se seu gráfico se repete a cada determinado intervalo. Esse intervalo é chamado de período.
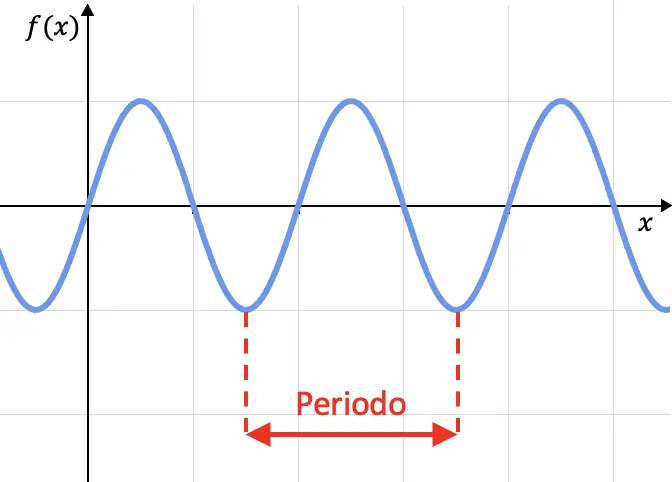
Matematicamente, uma função é definida como periódica se for cumprida apenas
![]()
para qualquer valor da variável independente x.
![]()
Onde T é o período da função periódica i k inteiro.
Exemplos de periodicidades de função
Depois de vermos o conceito de periodicidade de uma função, veremos vários exemplos de como calcular a periodicidade de uma função.
Exemplo 1
Determine se a seguinte função é periódica:
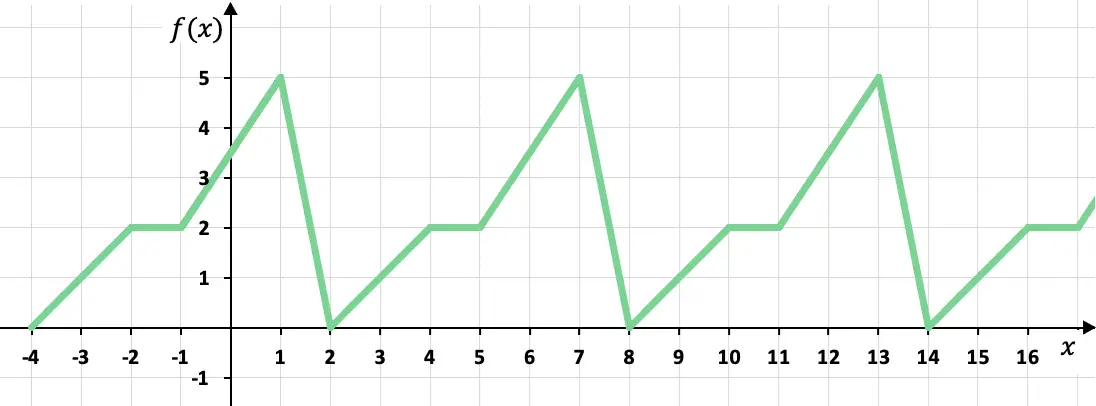
Esta função definida por partes é uma função periódica, pois os valores de seu gráfico se repetem ciclicamente. Mais precisamente, a função assume o mesmo valor a cada seis x, portanto, o período da função é igual a 6.
![]()
Exemplo 2
Encontre a periodicidade da seguinte função:
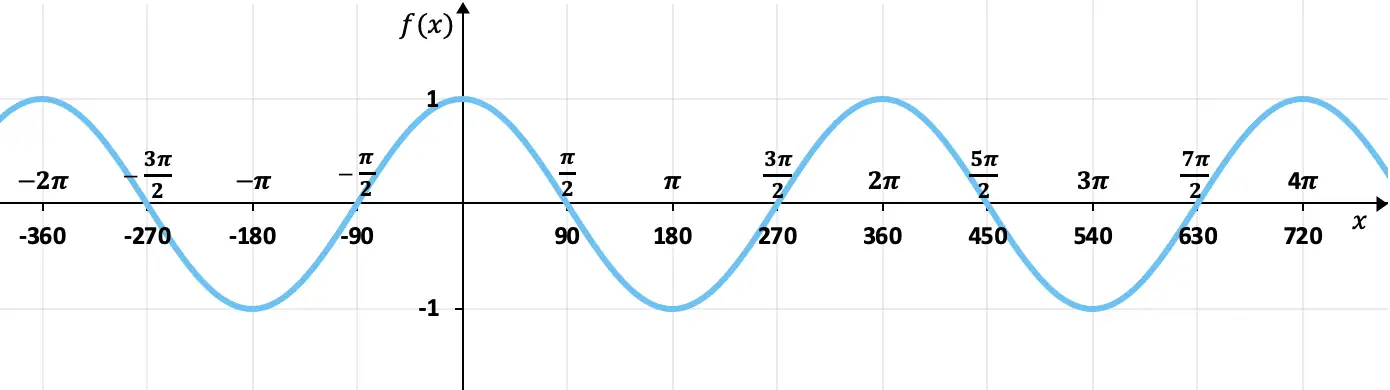
Esta função corresponde à representação gráfica de uma função trigonométrica, mais precisamente a função cosseno.
Como podemos ver no gráfico, a função repete seus valores periodicamente, portanto é uma função periódica. Além disso, entre o pico e o pico da onda existe um espaço de 2π (ou 360º), então este é o período da função.
![]()
Periodicidade das funções trigonométricas
A periodicidade e as funções trigonométricas estão intimamente relacionadas, aliás, uma das principais características deste tipo de funções é que a maioria das funções trigonométricas são periódicas.
A seguir estudaremos a periodicidade das 3 principais funções trigonométricas: seno, cosseno e tangente.
Período da função senoidal
A expressão para a função seno é a seguinte:
![]()
Neste caso, não é necessário representar graficamente a função para encontrar o seu período, mas pode ser calculado simplesmente aplicando a seguinte fórmula:
![]()
Além disso, a função seno tem a particularidade de que se alterarmos o seu período, também alteramos a forma do seu gráfico. Você pode ver como o valor do período afeta sua representação gráfica no seguinte link:
➤ Veja: Gráfico da função seno
Período da função cosseno
A expressão algébrica para a função cosseno é a seguinte:
![]()
Tal como acontece com o seno, o período da função cosseno pode ser encontrado diretamente usando a seguinte fórmula:
![]()
O valor do período cosseno determina completamente o seu gráfico, clique no link a seguir e descubra o porquê:
➤ Veja: Gráfico da função cosseno
Período da função tangente
A função tangente é descrita matematicamente:
![]()
O período da função tangente é calculado com a mesma fórmula do seno e do cosseno:
![]()
No entanto, o gráfico da função tangente é diferente do seno e do cosseno porque também possui assíntotas que se repetem periodicamente. Você pode ver esta e outras características desta função trigonométrica no seguinte link:
➤ Veja: Gráfico da função tangente