Operações com monômios

setembro 17, 2023

Nesta página explicamos como realizar todas as operações com monômios (adição, subtração, multiplicação, divisão e potência). Além disso, você poderá ver exemplos de cada tipo de operação com monômios e praticar com exercícios resolvidos passo a passo.

Adição e subtração de monômios

Dois ou mais monômios só podem ser adicionados ou subtraídos se forem monômios semelhantes, ou seja, se os dois monômios tiverem parte literal idêntica (mesmas letras e mesmos expoentes).

Então, a soma (ou subtração) de dois monômios semelhantes é igual a outro monômio composto pela mesma parte literal e a soma (ou subtração) dos coeficientes desses dois monômios.

A adição e subtração de monômios também são chamadas de adição e subtração de monômios, respectivamente.

Exemplos de adição e subtração de monômios

Para que você entenda claramente como somar e subtrair dois ou mais monômios, deixamos abaixo vários exemplos:

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

Os monômios do último exemplo não podem ser somados ou subtraídos porque não são semelhantes ou, em outras palavras, têm incógnitas ou expoentes diferentes.

Produto de um número de vezes um monômio

Para resolver o produto de um monômio por um número, basta multiplicar o coeficiente do monômio por esse número, deixando a parte literal do monômio igual.

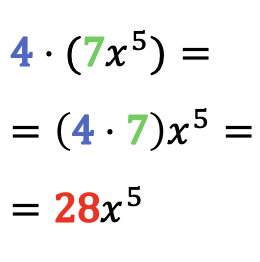
Exemplos de multiplicação de números por monômios

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

Multiplicação de monômios

O resultado da multiplicação de dois monômios é outro monômio cujo coeficiente é o produto dos coeficientes dos monômios e cuja parte literal é obtida multiplicando as variáveis que têm a mesma base, ou seja, somando seus expoentes.

Portanto, para multiplicar dois monômios diferentes, devemos multiplicar os coeficientes entre eles e somar os expoentes das potências que possuem a mesma base.

No entanto, se multiplicarmos dois monômios com potências de base diferentes , precisamos simplesmente multiplicar seus coeficientes e deixar as potências iguais. Por exemplo:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Por outro lado, na multiplicação de monômios, deve-se levar em consideração a regra dos sinais:

Um monômio positivo multiplicado por um monômio positivo dá outro monômio positivo.
Um monômio positivo multiplicado por um monômio negativo (ou vice-versa) é igual a um monômio negativo.
Dois monômios negativos multiplicados dão origem a um monômio positivo.

Exemplos de multiplicações monomiais

Abaixo estão vários exemplos de multiplicação entre monômios para que você possa ver como isso é feito:

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Como você viu, resolver uma multiplicação de monômios é relativamente simples. Mas você deve ter em mente que monômios também podem ser multiplicados por polinômios, e até 2 ou mais polinômios podem ser multiplicados juntos. Se você estiver mais interessado, pode ver como funcionam todas essas operações clicando em multiplicação polinomial .

Divisão de monômios

Em matemática, o resultado da divisão dos monômios é outro monômio cujo coeficiente equivale ao quociente dos coeficientes dos monômios e cuja parte literal é obtida dividindo as variáveis que têm a mesma base, ou seja, subtraindo seus expoentes .

Obviamente, qualquer divisão de monômios também pode ser expressa como uma fração:

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

Assim como na multiplicação, na divisão dos monômios é necessário aplicar a lei dos sinais:

Um monômio positivo dividido por um monômio positivo dá outro monômio positivo.
Um monômio positivo dividido por um monômio negativo (ou vice-versa) é equivalente a um monômio negativo.
Dois monômios negativos divididos entre si dão origem a um monômio positivo.

Exemplos de divisão de monômios

Você pode ver mais exemplos de como dois ou mais monômios são divididos abaixo:

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Certamente em algum momento, quando você aprendeu algo novo em matemática, você se perguntou: para que serve ? Bem, a divisão monomial é usada para dividir polinômios. Na verdade, é bastante comum cometer um erro ao dividir polinômios porque dois monômios foram divididos incorretamente. Por isso recomendamos que, agora que você está familiarizado com a divisão entre monômios, veja como se calcula a divisão de polinômios , pois agora será muito mais fácil aprender o procedimento (é bastante complicado).

Poder de um monômio

Em matemática, para calcular a potência de um monômio, cada elemento do monômio é elevado ao expoente da potência . Ou seja, a potência de um monômio consiste em elevar seu coeficiente e suas variáveis (letras) ao expoente da potência.

como as operações com monômios são resolvidas

Lembre-se das propriedades das potências que quando ambos elevam um termo já alto, os expoentes se multiplicam. É por isso que, elevado à potência de um monômio, o expoente de cada letra é sempre multiplicado pelo expoente que indica a potência .

Por outro lado, para realizar corretamente esta operação é necessário lembrar a seguinte propriedade das potências:

Um monômio negativo elevado a um expoente par é equivalente a um monômio positivo.
Em vez disso, um monômio negativo elevado a um expoente ímpar resulta em um monômio negativo.

Exemplos de potências de monômios

Deixamos alguns exemplos para que você possa entender claramente como se calcula a potência de um monômio:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Operações combinadas com monômios

Depois de ver o que são todas as operações com monômios, saiba que elas também podem ser combinadas entre si. Ou seja, podemos encontrar exercícios em que somos solicitados a resolver operações com monômios onde estão envolvidos todos os tipos: adição, subtração, multiplicação, divisão e potências.

Mas não se preocupe, eles não são tão difíceis quanto parecem. A única coisa que você precisa lembrar é a ordem em que as operações combinadas são resolvidas:

Primeiro, são resolvidas as operações com monômios entre parênteses.
Então as potências dos monômios são calculadas.
Terceiro, são realizadas multiplicações e divisões de monômios.
E, finalmente, são determinadas as adições e subtrações de monômios.

Tenho certeza que resolvendo um exemplo você verá com mais clareza:

Exemplo de operação combinada de monômios

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

Primeiramente devemos resolver as operações com monômios entre parênteses:

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

Neste caso, não temos poder. Então agora vamos calcular as multiplicações e divisões de monômios:

$-2x^5+18x^5 - 7x^5$

E finalmente, adicionamos e subtraímos monômios:

$16x^5 - 7x^5$

$\bm{9x^5}$

Exercícios resolvidos sobre operações com monômios

Caso queira praticar, deixamos abaixo vários exercícios resolvidos passo a passo da dificuldade ESO sobre operações com monômios.

Exercício 1

Calcule as seguintes adições e subtrações de monômios:

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

Veja a solução

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

Exercício 2

Resolva as seguintes multiplicações de monômios:

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

Veja a solução

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”> <div class=$

Exercício 3

Determine o resultado das seguintes divisões de monômios:

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

Veja a solução

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

Na operação anterior simplificamos o termo

$y^0$

porque qualquer número elevado a 0 é igual a 1. Então:

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”> <div class=$

Exercício 4

Encontre as seguintes potências de monômios:

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

Veja a solução

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Exercício 5

Resolva as seguintes operações combinadas com monômios e simplifique o máximo possível:

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

Veja a solução

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

A operação não pode ser simplificada ainda mais porque os dois monômios têm expoentes diferentes, então o resultado é um polinômio.

Se você chegou até aqui, significa que já dominou todas as operações com monômios. Brilhante! Pois bem, outra operação que certamente lhe interessará é o fatorial de um número. Esta é uma operação bastante curiosa, pois é calculada de forma diferente das demais. E, de fato, muitas pessoas não sabem o que é o fatorial de um número. Descubra como resolver um fatorial clicando neste link.

Adição e subtração de monômios

Exemplos de adição e subtração de monômios

Produto de um número de vezes um monômio

Exemplos de multiplicação de números por monômios

Multiplicação de monômios

Exemplos de multiplicações monomiais

Divisão de monômios

Exemplos de divisão de monômios

Poder de um monômio

Exemplos de potências de monômios

Operações combinadas com monômios

Exemplo de operação combinada de monômios

Exercícios resolvidos sobre operações com monômios

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta