Neste artigo explicamos quais operações podem ser realizadas com funções. Você poderá ver a explicação e também exercícios resolvidos sobre operações com funções. E por fim, você encontrará as propriedades das operações com as funções.
O que são operações com funções?
Você pode realizar 5 tipos diferentes de operações com funções: adição, subtração, produto, divisão e composição. Ou seja, duas funções podem ser somadas, subtraídas, multiplicadas, divididas ou compostas.
A seguir veremos como é realizado cada tipo de operação com funções e as características de cada uma delas.
Soma de funções
O valor da soma (ou adição) de duas funções é igual à soma do valor de cada função. Ou seja, para calcular a imagem de uma função soma, basta somar as imagens das funções envolvidas na operação.
![]()
Além disso, o domínio da soma de duas funções é a intersecção do domínio de cada função somada.
![]()
Vamos ver como duas funções são adicionadas usando um exemplo:
![]()
Primeiro adicionamos as duas funções:
![]()
E agora encontramos o domínio da função soma. Para fazer isso, calculamos o domínio de cada função separadamente:
![]()
➤ Veja: como calcular o domínio de uma função
Então, o domínio da função resultante da operação será:
![]()
Cada operação com funções deve vir acompanhada de seu domínio para definir completamente o resultado.
Subtração de funções
A imagem da subtração (ou diferença) de duas funções é a subtração das imagens de cada função participante da operação:
![]()
Tal como acontece com a função de adição, o domínio de subtração de duas funções é equivalente à intersecção do domínio de cada função.
![]()
Assim, se uma função não for definida em um determinado valor da variável independente x, a função resultante da subtração também não será definida.
Vamos ver como duas funções são subtraídas através de um exemplo:
![]()
Primeiro subtraímos as duas funções:
![]()
E então determinamos o domínio da função de subtração:
![]()
![]()
Produto principal
Para calcular o produto ou (a multiplicação) de duas funções , basta multiplicar as expressões de cada função.
![]()
Por outro lado, o domínio da função produto é o conjunto de interseções do domínio de cada função multiplicada.
![]()
Por exemplo, se tivermos as duas funções a seguir:
![]()
Primeiramente realizamos o funcionamento do produto com as duas funções:
![]()
E, por fim, encontramos o domínio da função resultante da operação:
![]()
![]()
Distribuição de funções
O resultado numérico de uma divisão (ou quociente) de duas funções corresponde à seguinte equação:
![]()
Porém, o domínio de divisão de duas funções é o conjunto de interseções do domínio de cada função menos todo o x que anula a função que atua como divisor, pois caso contrário obteríamos uma indeterminação.
![]()
Como exemplo, dividiremos as seguintes funções:
![]()
A distribuição das funções é a seguinte:
![]()
Por outro lado, o domínio de cada função separadamente consiste em todos os números reais
![]()
Porém, como não pode haver zero no denominador de uma fração, no domínio da função resultante devemos retirar todos os valores que anulam o denominador (x=3).
![]()
Composição de funções
A composição de funções é a operação mais difícil de resolver, pois é o conceito mais complicado.
A composição de funções consiste na aplicação sucessiva de duas funções. Algebricamente, a composição de duas funções é expressa da seguinte forma:
![]()
Por outro lado, o domínio de composição de funções
![]()
é equivalente ao conjunto de todos os valores de x no domínio da função
![]()
como
![]()
pertence ao domínio da função
![]()
![]()
Por exemplo, dadas as duas funções a seguir:
![]()
Para encontrar a função composta
![]()
seguido pela
![]()
precisamos substituir a expressão de
![]()
onde há um
![]()
na expressão de
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
Neste caso, o domínio de ambas as funções consiste inteiramente em números reais, portanto o domínio da função composta também consistirá em números reais.
![]()
Como você pode ver, compor funções não é uma operação simples de entender. Portanto, recomendamos que você pratique os seguintes exercícios de composição de funções:
➤ Veja: exercícios resolvidos sobre composição de funções
Propriedades de operações com funções
De todas as operações com funções, a soma e o produto são caracterizados pelas seguintes propriedades:
- Propriedade associativa : A ordem em que 3 ou mais funções são adicionadas ou multiplicadas é irrelevante.
![]()
![]()
- Propriedade comutativa : a ordem de adição ou multiplicação de duas funções não modifica o resultado.
![]()
![]()
- Elemento neutro: a operação de soma e a operação de produto têm funções de elemento neutro constantes
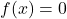
E
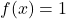
respectivamente.
- Elemento simétrico : a função soma tem a função oposta
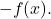
- Propriedade distributiva : esta propriedade liga a soma e o produto das operações, e baseia-se na seguinte igualdade:
![]()