O que são e como calcular as componentes de um vetor

Nesta página você encontrará a explicação de quais são os componentes (ou coordenadas) de um vetor. Além disso, você poderá ver como eles são calculados a partir de dois pontos e até como são decompostos através de seu módulo e ângulo. Além disso, você encontrará exemplos e exercícios resolvidos passo a passo.

Quais são os componentes de um vetor?

Os componentes de um vetor são as projeções de um vetor nos eixos cartesianos. Portanto, a projeção do vetor no eixo x é a componente X do vetor e, da mesma forma, a projeção do vetor no eixo y é a componente Y do vetor.

Os componentes de um vetor também podem ser chamados de coordenadas de um vetor.

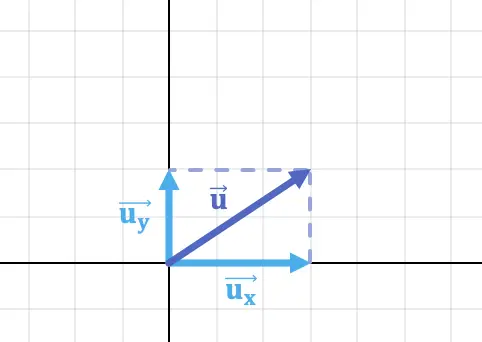
Por exemplo, a componente horizontal e a componente vertical do vetor na imagem acima são:

$\vv{\text{u}}_x = 3$

$\vv{\text{u}}_y = 2$

Então o vetor é:

$\vv{\text{u}} =(3,2)$

Portanto, os componentes de um vetor também podem ser definidos como a representação de um vetor em um sistema de coordenadas. Obviamente, se for um sistema bidimensional (em r2) o vetor terá duas componentes, por outro lado, se for uma base tridimensional (em r3) o vetor será composto por três componentes.

As componentes cartesianas de um vetor são tão importantes porque com elas podemos conhecer as características do vetor, que são principalmente a direção, sentido e módulo (ou magnitude) do vetor. Além disso, eles são usados para realizar operações vetoriais.

Como calcular as componentes de um vetor a partir de dois pontos

Acabamos de ver como determinar graficamente as coordenadas de um vetor, porém, também podemos determinar numericamente suas componentes.

Para calcular numericamente as componentes de um vetor, precisamos conhecer dois pontos: sua origem e seu fim, ou seja, onde começa e onde termina. Já as componentes de um vetor são as coordenadas que obtemos subtraindo seu final menos sua origem.

$\vv{AB} = B -A$

Por exemplo, calcularemos o vetor cuja origem é o ponto A(3,1) e seu final é o ponto B(5,4):

$A(3,1) \qquad B(5,4)$

$\begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}$

Como você pode ver, determinar os componentes de um vetor não é muito difícil, porém é bastante importante. Por exemplo, um dos tipos de vetores mais comumente usados são vetores perpendiculares (ou ortogonais); Bem, se você entende quais são as coordenadas de um vetor, é muito fácil calcular vetores perpendiculares. Você pode ver como isso é feito na explicação dos vetores ortogonais .

Como calcular os componentes de um vetor a partir de seu módulo e ângulo

Você também pode encontrar as componentes de um vetor a partir de sua magnitude e do ângulo que ele forma com o eixo X. Este processo é chamado de decomposição vetorial .

Assim, os componentes X e Y do vetor podem ser calculados com as razões trigonométricas do cosseno e do seno:

Como você pode ver na imagem, o módulo de um vetor e seus componentes completam um triângulo retângulo, portanto as fórmulas elementares da trigonometria podem ser aplicadas.

Se você não se lembra como o módulo de um vetor é calculado, você pode pesquisar qual é o módulo de um vetor . Aqui você encontrará a fórmula da magnitude de um vetor, bem como exemplos, exercícios resolvidos passo a passo e todas as propriedades da magnitude de um vetor. Esta é uma explicação muito completa, então você a entenderá perfeitamente. ✅

Ao contrário da magnitude de um vetor que é sempre positivo, suas componentes podem ser negativas porque o seno e o cosseno podem assumir valores negativos.

Como exemplo, faremos a decomposição vetorial do vetor cujo módulo e ângulo com o eixo OX são:

$\lvert \vv{\text{u}} \rvert = 8 \qquad \alpha = 60º$