O número de Euler (também conhecido como constante de Euler) é um número matemático importante e essencial em várias áreas da matemática, incluindo teoria dos números, topologia, teoria dos grupos e teoria das funções. É representado pela letra grega “e” e seu valor aproximado é 2,71828.
O número e segue da fórmula da função exponencial e é um número fundamental na teoria dos números complexos.
É também um número natural que aparece na resolução de muitos problemas matemáticos, incluindo cálculo de probabilidade e modelagem de processos de crescimento e decaimento.
Qual é a origem do número de Euler?
O número de Euler deve o seu nome ao matemático suíço Leonhard Euler (1707-1783), que foi um dos maiores matemáticos de todos os tempos e é considerado o pai da matemática moderna.
Euler fez contribuições valiosas para muitas áreas da matemática, incluindo teoria dos números, geometria, cálculo, física e astronomia.
Foi ele quem primeiro definiu e utilizou o número e (chamado número de Euler) em seu trabalho sobre cálculo e teoria dos logaritmos. A fórmula de Euler para números complexos é também uma de suas contribuições mais notáveis para a matemática.
Como esse valor é obtido?
Na verdade, existem vários métodos para calcular o número de Euler. Porém, vale ressaltar que nenhum dos métodos dá um resultado exato. Portanto, sua numeração é contínua e infinita, mas não se repete.
Na verdade, atualmente são conhecidos mais de 1 trilhão de números que compõem a figura do número e. A série infinita que define o número de Euler é:

Ouro “!” é fatorial, que é definido como o produto de todos os números naturais até esse número. Por exemplo:
5! = 5 4 3 2 1 = 120
Podemos ver esta série graficamente como a soma de uma série de retângulos de altura 1 e largura decrescente, onde a largura de cada retângulo é 1/n!, onde n é o número de fatoriais.
Se aumentarmos o número de retângulos na soma, a aproximação da área sob a curva da função exponencial fica cada vez mais próxima do número de Euler.
Em resumo, o número de Euler é um número que resulta da soma de uma série infinita e é fundamental para muitas áreas da matemática. Embora seja um número irracional , seu valor aproximado é 2,71828.
É importante ter em mente que o próprio Euler implementou este método para calcular e com 18 casas decimais.
Outra forma de calculá-lo:
Podemos calcular o valor aproximado do número de Euler em uma reta usando uma série de termos finitos . Por exemplo, se tomarmos a primeira série infinita definida acima:

Podemos calcular o valor aproximado somando os primeiros termos da série. Por exemplo, se somarmos os primeiros 6 termos:
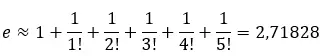
Podemos traçar esta série em uma reta para ver como ela se aproxima do valor aproximado de 2,71828 .
Graficamente, a linha que representa o número de Euler pode ser desenhada como uma série de retângulos de altura 1 e largura decrescente, onde a largura de cada retângulo é 1/n!, onde n é o número de fatoriais.
Se aumentarmos o número de retângulos na soma, a aproximação da área sob a curva da função exponencial fica cada vez mais próxima do número de Euler.
Equações exponenciais com número de Euler
Equações exponenciais com o número de Euler podem ser utilizadas para modelar uma ampla variedade de fenômenos em ciências como física, biologia, economia, entre outras. aqui estão alguns exemplos:
Crescimento e decadência exponencial
Este modelo descreve a taxa à qual uma população cresce ou diminui , ou a taxa à qual uma substância tóxica se decompõe.
Por exemplo, se uma população cresce a uma taxa de 5% ao ano, o seu tamanho pode ser descrito pela fórmula:
P(t) = P0 · e 0,05t , onde P0 é o tamanho inicial da população.
Modelos de decaimento radioativo
Este modelo descreve a taxa na qual os átomos radioativos decaem ao longo do tempo.
A fórmula é a seguinte:
N(t) = N0 e -λt
onde N0 é o número inicial de átomos, λ é uma constante que depende do material radioativo e t é o tempo.
Estes são apenas alguns exemplos de como equações exponenciais com número de Euler podem ser usadas na prática. Existem muitas outras áreas onde as equações exponenciais são úteis e relevantes.
Quais são as aplicações do número de Euler?
O número de Euler tem uma ampla gama de aplicações em diferentes áreas da matemática e das ciências. Alguns dos campos em que o número e é usado são:
- Cálculo e análise matemática : é utilizado no estudo de funções exponenciais e logarítmicas, e na resolução de equações diferenciais.
- Teoria dos números – utilizada no estudo da distribuição dos números primos e na resolução de problemas relacionados à teoria dos números.
- Probabilidade e Estatística : É utilizado na resolução de problemas relacionados à distribuição de probabilidade e estimativa de valores esperados.
- Criptografia – Usada no estudo de algoritmos de criptografia e descriptografia.
- Física – usada para resolver problemas relacionados à termodinâmica, mecânica quântica e física estatística.
- Química : é utilizada na resolução de problemas relacionados à termodinâmica química e à cinética química.
Fórmula de Euler para números complexos
A fórmula de Euler para números complexos estabelece uma relação entre funções trigonométricas e exponenciais. A fórmula está escrita:

Onde “e” é a base dos logaritmos naturais, “i” é a unidade imaginária, “x” é um número real e “cos” e “sin” são as funções trigonométricas cosseno e seno, respectivamente.
Esta fórmula é muito útil em muitas áreas da matemática, incluindo teoria dos números, teoria das funções e teoria da complexidade, e tem uma ampla variedade de aplicações em engenharia, física e economia.
Um exemplo prático de sua utilização está na representação de sinais e sistemas na análise de Fourier, em que sinais periódicos são representados como uma soma de sinais senoidais complexos.
A fórmula de Euler é usada para descrever como esses sinais complexos se relacionam com as funções trigonométricas reais que descrevem os sinais senoidais individuais.
Número de Euler e juros compostos
Juros compostos são um conceito financeiro que descreve o processo pelo qual uma quantia em dinheiro, chamada principal, rende juros sobre juros que aumentam com o tempo.
Ou seja, os juros auferidos com um investimento provêm não só do capital inicial, mas também dos juros auferidos em períodos anteriores.
O número de Euler e os juros compostos estão relacionados porque a fórmula para calcular os juros compostos usa o número de Euler. A fórmula dos juros compostos é:
A = P e rt
Onde A é o valor final, P é o principal, r é a taxa de juros, t é o tempo e e é o número de Euler. Desta forma, o número de Euler é um fator importante na formulação matemática para cálculo de juros compostos.
Um exemplo de cálculo de juros compostos com números concretos seria:
Suponhamos que temos um investimento de 1.000€ a uma taxa de juro de 5% ao ano durante 2 anos. A fórmula para calcular juros compostos seria:
A = P e rt = 1000 e 0,05 2 = 1000 1,1025 = 1102,5€.
Isto significa que após 2 anos, o nosso capital inicial de 1.000€ terá aumentado para 1.102,5€ graças aos juros compostos gerados.
Exemplos de exercícios matemáticos com o número de Euler
Aqui estão dois exemplos de problemas matemáticos resolvidos envolvendo o número de Euler:
1. Encontre o valor de “e ix ” onde x é um número real:
A identidade de Euler nos diz que e ix = cos(x) + i · sin(x). Portanto, se soubermos o valor de x, podemos calcular o valor de e ix utilizando funções trigonométricas.
2. Calcule e^(x 2 ) para um determinado valor de x:
Podemos usar a série de Taylor para calcular o valor de e^(x 2 ). A série de Taylor de e x é uma expansão infinita que permite calcular aproximações sucessivas do valor de e x , dependendo do termo utilizado.

Se substituirmos x 2 por x nesta série, obteremos a série de Taylor para e^(x 2 ).