Você já se perguntou como os números racionais diferem de outros números? Neste artigo, exploraremos em profundidade os números racionais, incluindo suas características e classificação únicas. Prepare-se para entender melhor o conceito!
O que são números racionais?
Os números racionais (ℚ) são uma subclasse de números reais que inclui todos os números que podem ser expressos como uma fração. Isso significa que números racionais são aqueles que podem ser escritos como uma razão de dois inteiros, a/b, onde b ≠ 0.
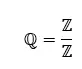
Os números racionais também podem ser expressos como números decimais repetidos ou finitos , porque são compostos por uma série de dígitos repetidos. Alguns exemplos de números racionais são 1/2, 3/4, 10/3, 2/3 e π (pi).
Subconjuntos de racionais
Os números racionais podem ser divididos em dois subconjuntos :
- Inteiros , que incluem 0, todos os números naturais e todos os números negativos.
- Números decimais ou números fracionários , que são todos aqueles que expressam valores formados por: uma parte inteira e uma parte decimal, esta última permite expressar valores menores que a unidade.

Outra subcategoria do conjunto dos reais são os números irracionais , que são um pouco mais complexos.
Exemplos de números racionais
Os números racionais são aqueles que podem ser expressos como fração, ou seja, como quociente de dois números inteiros. Aqui estão alguns exemplos de números racionais:
-23
-4/5
-1/2
-7/9
Todas as frações que representam um número inteiro são igualmente racionais. Por exemplo:
-1/1
-2/2
-3/3
Propriedades dos números racionais
A principal característica dos números racionais é que eles sempre possuem um denominador diferente de zero .
A segunda propriedade deste conjunto é que cada número racional pode ser representado por uma infinidade de frações equivalentes . Por exemplo, o número racional 3,5, que é igual a 7/2, também pode ser escrito 14/4, 28/8…, e uma infinidade de outras frações.
Os números racionais também satisfazem a propriedade distributiva . Isso significa que multiplicar ou dividir uma fração por outra não afetará o resultado:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (anúncio)/(bc)
Representação de números racionais
Os números racionais podem ser representados de diversas maneiras, mas a mais comum é como uma fração . Uma fração é composta por dois números: o numerador e o denominador.
O numerador indica quantas partes do todo são consideradas, enquanto o denominador indica quantas partes iguais existem no todo. Por exemplo, se um bolo for dividido em oito fatias iguais e três dessas fatias forem comidas, a fração que representa a quantidade de bolo consumida seria 3/8.
Outra forma de representar números racionais é por meio de decimais . Decimais são uma forma abreviada de escrever uma fração onde o denominador é um número 10, 100, 1000, etc. Por exemplo, se você tiver 1/4 de uma torta, isso pode ser expresso como 0,25 (significando “0 inteiros e 25/100”).
Porém, se quisermos representá-los graficamente, também podemos escrevê-los na reta numérica , na qual a ordem dos números pode ser vista muito bem. A seguir, mostramos um exemplo desta linha :
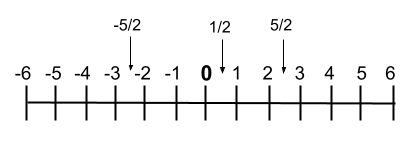
operações racionais
As operações fundamentais dos números racionais são as mesmas dos inteiros: adição, subtração, multiplicação e divisão. Se quiser aprender como resolver este tipo de operações, recomendamos a leitura do nosso artigo sobre operações com frações .
Porém, se você estiver trabalhando com números racionais com base decimal, deverá seguir o procedimento de resolução de operações que utiliza ao lidar com valores decimais .
Conclusão sobre o conjunto dos números racionais
Após esta exaustiva explicação, podemos concluir que o conjunto dos números racionais é um dos mais importantes da matemática. Contém todos os números que podem ser representados como fração, o que nos permite expressar quantidades com muita precisão.