Você provavelmente já ouviu falar de números complexos . Eles são talvez o conjunto de números mais difícil de lidar, porque combinam números reais e imaginários. Sua unificação permite estudar comportamentos numéricos que não podem ser tratados com todos os números reais.
O que são números complexos?
Os números complexos são a combinação de um número real e um número imaginário . Por exemplo, 4 + 5i é um número complexo que possui uma parte real igual a 4 e uma parte imaginária igual a 5i. Em geral, podemos expressá-los pela seguinte fórmula:
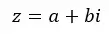
Onde, Re(z) = a e Im(z) = b
Como bem dissemos, os complexos são o maior conjunto ou conjunto global , que inclui tanto os números reais como os números imaginários. A seguir, mostramos um pequeno diagrama da estrutura hierárquica de todos os conjuntos:

Portanto, quando temos uma combinação de um número real e um número imaginário, temos um número complexo. Mas há momentos em que uma das duas partes é igual a zero. O que acontece nesses casos? Bem, ainda estamos lidando com complexos, porque o conjunto complexo abrange todos os outros conjuntos numéricos. Mas, entramos em uma subcategoria diferente:
| número complexo | festa real | parte da imaginação | Subcategoria |
| 2+5i | 2 | 5i | Complexo |
| 4 | 4 | 0 | puro real |
| 3i | 0 | 3i | Pura Imaginação |
Quando temos um real puro, como o valor imaginário b é igual a zero, o número complexo restante equivale a:
z = uma + 0i = uma
Por outro lado, quando temos imaginação pura, a é igual a zero e, consequentemente, o número complexo permanece o seguinte:
z = 0 + bi = bi
Representação gráfica de números complexos
Para representar números complexos, usamos o plano complexo . Que é composto por duas linhas : a linha real e a linha imaginária. Essas duas retas numéricas são usadas para localizar graficamente os números de cada conjunto e se os juntarmos, obtemos um plano, como:

O eixo X é chamado de eixo real porque é onde estão localizados os valores reais das peças. Embora o eixo Y seja chamado de eixo imaginário, é aqui que os valores imaginários são escritos. Vejamos um exemplo, colocaremos o número 3 + 2i no plano complexo.

Como você viu na imagem, localizamos o número usando os números 3 e 2 como coordenadas, cada um para um eixo. Se você quiser saber mais sobre como representar números complexos, recomendamos a leitura deste artigo.
Quais são os tipos de números complexos?
Agora veremos as maneiras que temos para expressar um número complexo. Até agora, vimos apenas a forma básica (chamada forma binomial), que é escrita como uma soma: parte real mais parte imaginária.
Mas, na realidade, temos três formas: a binomial, a polar e a trigonométrica . Cada tipo de expressão tem suas propriedades e é utilizada em uma situação ou outra. Então vamos explicar todos eles e mostrar como passar de um para o outro.
1. Forma binomial
Os números complexos na forma binomial são escritos como a soma da parte real e da parte imaginária: a + bi. Por exemplo, o número 6 + i é um complexo expresso em notação binomial. Neste, a fórmula é sempre a mesma:

Portanto, para expressar um número complexo na forma binomial, basta saber seu valor real e seu valor imaginário.
Por exemplo, o valor 3 + 2i está na forma binomial e, como vimos anteriormente, é representado da seguinte forma:

A forma binomial é usada principalmente para resolver adição e subtração de números complexos.
2. Forma polar
Para expressar números complexos na forma polar , devemos calcular seu módulo |z| e seu argumento. A forma polar é usada principalmente quando precisamos resolver multiplicação e divisão de números complexos.
Para calcular o módulo do número complexo, basta fazer o módulo de aeb, conforme explicado na seguinte fórmula:

E para calcular o argumento ou ângulo de z, precisamos calcular o arco tangente de b entre a:

É importante ressaltar que para determinar exatamente o valor do ângulo α é necessário identificar em qual quadrante ele está localizado. Na verdade, a função arco tangente calcula apenas ângulos entre π/2 e -π/2. Para especificar em qual quadrante está localizado o número complexo, devemos observar os valores a e b (se são positivos ou negativos):
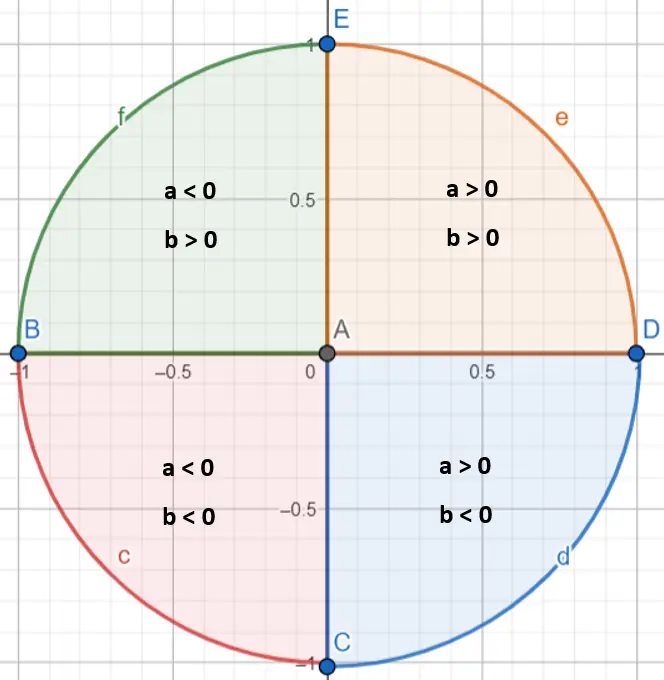
Depois de sabermos em qual quadrante nosso número se enquadra, precisamos seguir algumas regras:
- Se o número complexo estiver no primeiro quadrante (a > 0 e b > 0), deixaremos o argumento como está.
- Se o número complexo estiver no segundo quadrante (a < 0 e b > 0), adicionaremos π ao argumento.
- Se o número complexo estiver no terceiro quadrante (a < 0 e b < 0), subtraímos π do argumento.
- Se o número complexo estiver no quarto quadrante (a > 0 e b < 0), adicionaremos 2π ao argumento.
Caso você não saiba do que estamos falando quando dizemos quadrante, aconselhamos que consulte nosso artigo sobre razões trigonométricas .
Depois de conhecermos a magnitude e o argumento de z, podemos expressar o número complexo na forma polar. Embora este formulário aceite diversas nomenclaturas, as duas principais são:

Por exemplo, se quisermos mudar o número 3 + 5i para polar, basta seguir o seguinte procedimento.
Primeiro calculamos o módulo:
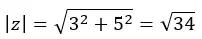
Aí calculamos o argumento, que está no primeiro quadrante, então fica como calculamos.
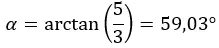
E expressamos o número na forma polar:
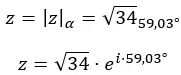
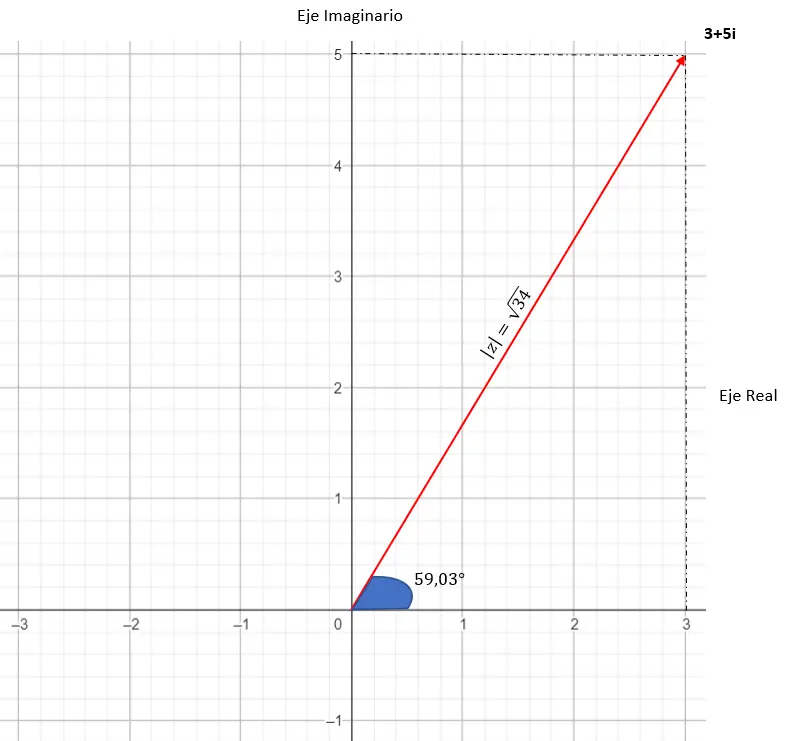
Sua representação gráfica é a seguinte:
3. Forma trigonométrica
Por fim, temos a notação trigonométrica , que é calculada a partir da fórmula de Euler :

Por exemplo, para expressar o número 4 – 3i na forma trigonométrica, seguimos o seguinte procedimento:
Começamos calculando o módulo e o argumento com as fórmulas que usamos na seção da forma polar.
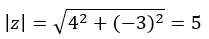
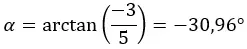
ATENÇÃO: O argumento está no quarto quadrante, pois (a > 0 e b < 0).
Adicionamos os dados à equação na forma trigonométrica.
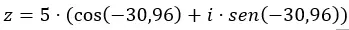
E já temos o número expresso na forma trigonométrica. Sua representação gráfica é a seguinte.
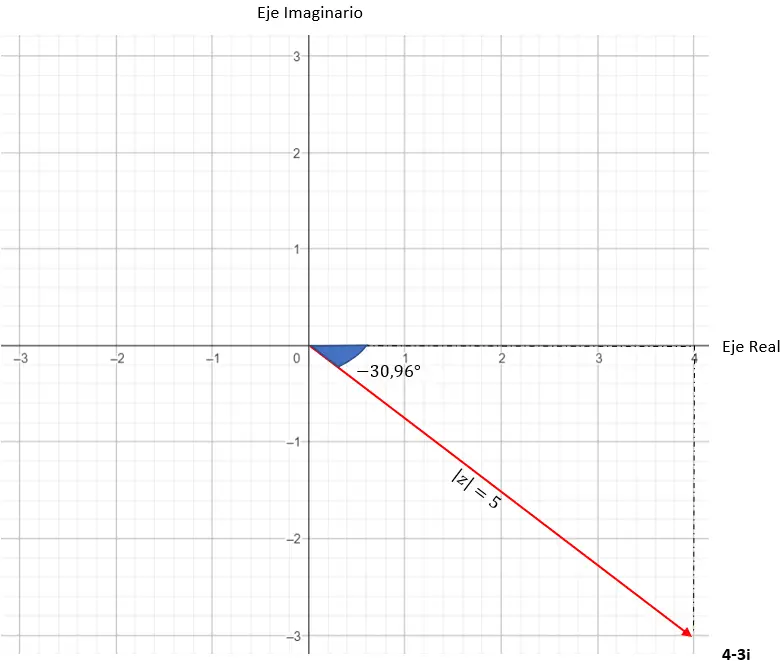
Como mudar de um tipo para outro?
Agora você conhece todas as maneiras de expressar um número complexo. E ao longo da última seção você pôde ver como acessar cada um deles, mas antes de terminarmos queremos dar um rápido resumo de como passar de um formulário para outro. Só você tem que usar as fórmulas que vimos na seção anterior.
Da forma binomial para polar e vice-versa
Para passar de binomial a polar, propomos o seguinte diagrama:
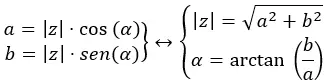
Vimos um exemplo anteriormente em que passamos de binomial para polar, então agora iremos de polar para binomial usando o diagrama acima. Precisamos converter √41 38,66 em um binômio.
Primeiro calculamos a.
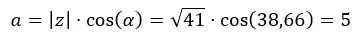
Então calculamos b.
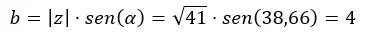
E expressamos isso na forma binomial.
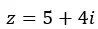
A representação gráfica deste número é assim:
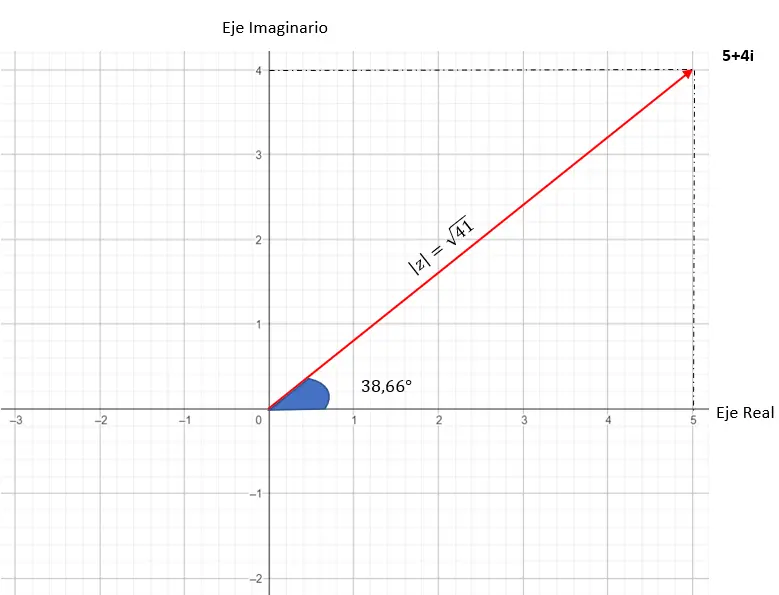
Da forma binomial para a forma trigonométrica e vice-versa
Para passar do binomial ao trigonométrico, você também deve aplicar as fórmulas de que falamos na seção anterior. Desta forma, primeiro calculamos o módulo e o argumento, depois colocamos esses dados na equação da forma trigonométrica. Para dar um exemplo, passaremos o número z = 3 + 2i trigonometricamente.
Primeiro calculamos o módulo e o argumento.
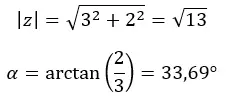
ATENÇÃO: O argumento está no primeiro quadrante, pois (a > 0 e b > 0).
Em seguida, completamos a equação da forma trigonométrica com esses dados.
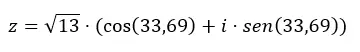
E se quisermos passar de trigonométrico para binomial, basta resolver a expressão anterior.
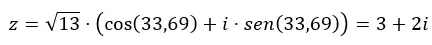
Da forma polar para a forma trigonométrica e vice-versa
Finalmente, passaremos da forma polar para a forma trigonométrica. O que é bastante simples, porque estas duas formas são expressas pelos mesmos dois valores: módulo e argumento . Então você só precisa preencher os formulários e pronto.
Vamos dar um exemplo, vamos converter o número z = √85 12,53 na forma trigonométrica.
Reformulamos as duas variáveis (módulo e argumento) na equação da forma trigonométrica:
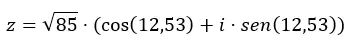
Então agora que você sabe como fazer a transição de uma forma para outra, recomendamos praticar um pouco com alguns exercícios . Desta forma você consolidará o conhecimento aprendido neste artigo. Se você tiver alguma dúvida sobre este assunto, fique à vontade para deixá-la nos comentários. E se você quiser saber mais sobre números complexos, confira os links abaixo.