A notação matemática é uma forma de comunicar ideias e cálculos através do uso de símbolos. Embora à primeira vista possa parecer confuso, com um pouco de prática você poderá interpretá-lo facilmente. Neste artigo mostraremos o significado de todos os símbolos utilizados nesta notação e alguns exemplos de como aplicá-los.
O que é notação matemática?
A notação matemática é uma forma de escrever valores e expressões usadas em matemática. Esta técnica permite aos matemáticos expor ideias de forma concisa e precisa . A notação matemática também permite que aqueles que praticam ou estudam matemática compreendam melhor os conceitos.
A linguagem da matemática não deve ser confundida com a notação científica, que é uma forma de escrever valores numéricos. Enquanto isso, a notação matemática é mais um conjunto de símbolos que permite escrever expressões complexas, assim como uma linguagem. Voltaremos a esse assunto com mais detalhes posteriormente.
Como ler notação matemática?
Aprender a interpretar a notação matemática é mais fácil do que parece, você só precisa aprender o significado de cada símbolo e, depois de fazer isso, será capaz de ler qualquer coisa escrita em notação matemática. É simples assim, embora obviamente exija prática e muito tempo de estudo.
As expressões matemáticas são muito lógicas e sempre seguem padrões, portanto, basta memorizar as regras e assim saberá como extrapolá-las para qualquer situação. Podemos até descrever cálculos muito complexos, esta é a magia da linguagem matemática, que permite comunicar de forma metódica mensagens muito elaboradas.
Componentes da notação matemática
A notação matemática é composta por uma série de símbolos que representam números, operações e as relações entre eles. Esses símbolos podem parecer complicados no início, mas com um pouco de prática e compreensão, a interpretação da notação matemática deve se tornar uma brincadeira de criança.
A seguir, explicaremos detalhadamente os quatro tipos de elementos que podem ser encontrados na linguagem matemática. Começando pelo mais básico e terminando pelo mais complexo e abstrato. E terminada a explicação teórica, falaremos sobre os tipos de notações numéricas que existem.
Números e conjuntos de números
Em primeiro lugar, devemos definir os números matemáticos , é um conceito matemático que designa uma quantidade relacionada a uma unidade. Podemos descrever qualquer valor numérico, seguindo o sistema de numeração decimal e combinando os seguintes símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
Se ordenarmos os números de acordo com propriedades diferentes, obteremos diversas categorias de números, chamadas conjuntos de números. E estes grupos de valores também possuem símbolos próprios que os designam, na lista a seguir apresentamos todos eles com o nome do grupo correspondente:
- ℙ: números primos
- ℕ: números naturais
- ℤ: Inteiro
- ℚ: números racionais
- ℝ: Números reais
- 𝕀: números imaginários
- ℂ: números complexos
- ℍ: Quatérnios
Esses símbolos são geralmente usados em nossos cálculos para determinar uma ampla gama de números, todos de uma vez. Por exemplo, se tivermos uma expressão que aceita muitos valores respectivamente, em vez de escrever os números um por um, será mais fácil especificarmos esses valores através do símbolo correspondente ao seu grupo numérico .
Operadores e quantificadores
Agora que discutimos os números, que são a essência da matemática, precisamos falar sobre operadores e quantificadores . Os primeiros são todos aqueles símbolos que nos permitem representar uma operação: adição (+), subtração (-), multiplicação (x ou ·), divisão (÷), entre outros.
Porém, também temos outros dois tipos de operadores, que são os operadores lógicos e os operadores relacionais. O primeiro expressa conjunção, disjunção e negação. Eles nos ajudam a propor operações lógicas , que, diferentemente das operações aritméticas, não funcionam com números, mas com proposições matemáticas.
Enquanto a segunda nos permite estabelecer equivalências e relações entre valores ou expressões matemáticas. Esses símbolos podem ser usados em cálculos aritméticos (para ordenar números), mas são mais importantes em álgebra, quando temos variáveis (mais sobre isso em duas seções).
Na lista a seguir você encontra a definição de todos os operadores que discutimos até agora:
| Símbolo | Definição | tipo |
| + | Adição | operador aritmético |
| – | Subtração | operador aritmético |
| X, *, · | Multiplicação | operador aritmético |
| ÷ | Divisão | operador aritmético |
| x² | fortalecimento | operador aritmético |
| √ | depósito | operador aritmético |
| E | Conjunção | operador lógico |
| QUALQUER | Disjunção | operador lógico |
| NÃO | Negação | operador lógico |
| = | Igual a | operador de relação |
| > | Maior que | operador de relação |
| < | Menor que | operador de relação |
| >= | Melhor que ou igual | operador de relação |
| <= | menos que ou igual a | operador de relação |
| ≠ | não é igual a | operador de relação |
| ≡ | Exatamente o mesmo | operador de relação |
| ≈ | quase igual | operador de relação |
| ≃ | Equivalente a | operador de relação |
| ∝ | Proporcional | operador de relação |
Embora existam também cinco outros operadores lógicos, que são usados para explicar a lógica matemática da teoria dos conjuntos. Que é um ramo que aplica lógica de conjunto , que é usado em cálculo, geometria, estatística… A seguir, mostramos os símbolos que são usados e sua definição.
| Símbolo | Definição |
| x ∈ UMA | x pertence a A |
| x ∉ UMA | x não pertence a A |
| ∪ | União |
| ∩ | Interseção |
| ⊂ | Inclusão |
Quanto aos quantificadores, podemos defini-los como símbolos que indicam o número de elementos de um conjunto que satisfazem uma determinada condição (equivalência, ordem, pertinência, etc.). Existe uma grande variedade de operadores, mas entre os mais utilizados podemos destacar:
| Símbolo | Definição | tipo |
| ∀x | para todo x | quantificar |
| ∃x | Existe pelo menos um x | quantificar |
| ∄x | não há x | quantificar |
| ∃!x | Existe apenas um x | quantificar |
| | | Como | quantificar |
| ∴ | ENTÃO | quantificar |
Expressões matemáticas e suas relações
Com os símbolos que cobrimos até agora, você pode entender muita matemática, mas ainda não explicamos suas aplicações ou relações em expressões complexas, como operações combinadas ou cálculos algébricos. Além disso, ainda existem símbolos de relacionamento para discutir. Esses são os que veremos nesta seção.
Começando pelos símbolos de agrupamento, eles são parênteses, colchetes e chaves. Estes elementos são essenciais na designação de fórmulas complexas. Sua principal função é dar prioridade a determinados cálculos, dentro de uma expressão global. E existem diferentes níveis de prioridade entre os três tipos. Nesta expressão você pode ver a ordem de escrita 3 {[2 + (3 – 2) · 2] – 4}.
| símbolos | Definição | Prioridade |
| “(“E”)” | Parêntese | Prioridade máxima |
| “[“E”]” | Colchetes | segunda prioridade |
| “{” E “}” | Chaves | terceira prioridade |
E para finalizar esta categoria falaremos sobre somatórios (Σ) e produtos (∏) , que são elementos que nos permitem descrever adições e multiplicações repetidas. O somatório equivale a dizer: “soma de Xi, onde i leva os valores de 1 a an”. E o produto é o mesmo, mas em vez de somar, multiplicamos.
análise algébrica
A primeira coisa a discutir sobre símbolos algébricos são as variáveis, que são representadas pelas letras do alfabeto. Sua função é imitar um número , mas não possuem um valor fixo como as constantes matemáticas , portanto podem assumir novos valores. Isso se aplica a equações, limites, derivadas, integrais, matrizes…
Por fim, queremos falar sobre as representações de todas essas operações algébricas de que acabamos de falar neste último parágrafo. Desde então, eles são a base da álgebra e você precisa saber qual é a sua simbologia. A seguir, mostramos uma tabela com seus diferentes símbolos e uma breve definição:
| Símbolo | Definição |
| lim x → b | Limite (quando x tende para b) |
| y’, ƒ’ (x), dy / dx | derivado |
| ∫ | Completo |
| Para mxn | Matriz de dimensões mxn |
Conclusão sobre os símbolos da linguagem matemática
Até agora você viu todos os símbolos importantes abordados na matemática, obviamente há mais para discutir. Mas, estas são mais específicas para cada subcategoria da matemática: geometria, estatística, álgebra… Encerraremos, portanto, este assunto e falaremos sobre notações numéricas.
Tipos de notações numéricas
Nesta seção veremos todas as formas de expressar números matemáticos, pois existem diferentes notações para fazê-lo. No início mencionamos acima o sistema de numeração decimal, que é o mais utilizado pelos matemáticos. A seguir, explicaremos com mais detalhes e mostraremos outros tipos de notação matemática:
notação decimal
O sistema numérico decimal é um sistema numérico posicional (sistema em que a posição de cada dígito determinará seu valor) é baseado nos múltiplos e submúltiplos do número 10. Já dez é o número usado como base numérica . Portanto, os dez símbolos numéricos que usaremos são: 1, 2, 3, 4, 5, 6, 7, 8, 9 e 0.
O valor desses números é determinado a partir da soma dos algarismos multiplicados pelas potências na base dez, estabelecida de acordo com a posição . E é muito importante que você lembre que para escrever um número menor que um é necessário usar a vírgula. Abaixo está um exemplo:
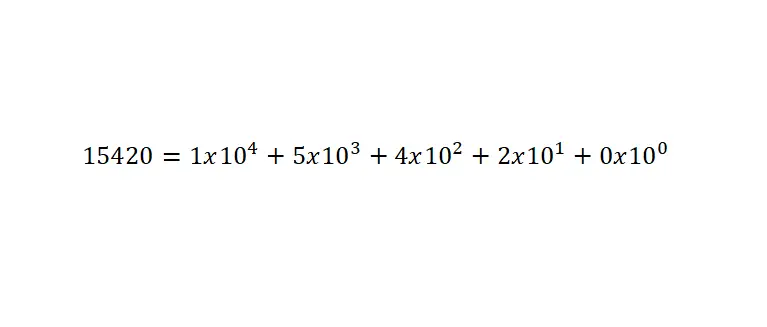
Notação científica
A notação de forma exponencial ou notação científica é claramente um dos tipos de escrita mais utilizados em ciência e tecnologia. Na verdade, isto permite-nos expressar números muito grandes e muito pequenos de uma forma simples. Para entender a definição de notação científica, explicaremos como passar um número inteiro para esta notação:
- Mova a vírgula: você deve mover a vírgula quantas vezes forem necessárias até chegar ao primeiro dígito (para a esquerda se tiver um número muito grande e para a direita se tiver um número muito pequeno).
- Estabeleça a base: escreva este último número multiplicado por dez, então, ao lado do valor que você obteve movendo a vírgula para um lado, você deve escrever uma multiplicação por dez: “x 10”.
- Adicione um expoente: com um valor igual ao número de vezes que você moveu a vírgula. Com números grandes, você deixará o expoente positivo, mas, com números pequenos, deverá escrevê-lo com sinal negativo.
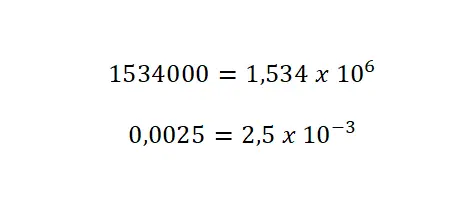
notação hexadecimal
O sistema hexadecimal é baseado em 16, o que significa que utiliza dezesseis símbolos diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F Como você pode veja bem, esse sistema de numeração é composto pelos números do sistema decimal e seis letras. Esta notação é geralmente usada principalmente em TI e em tudo relacionado a TI.
É importante esclarecer que por possuir símbolos em comum com outros tipos de notação, devemos sempre indicar que está escrito em hexadecimal por meio de parênteses e do índice 16 . No exemplo a seguir você pode ver a partir de um exemplo muito claro a conversão de um número hexadecimal em notação decimal:
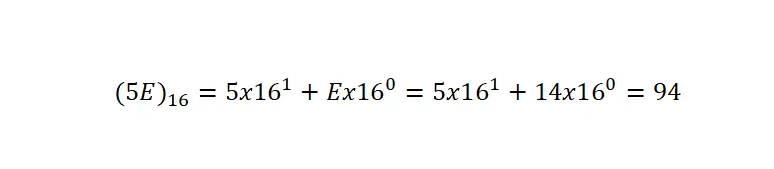
Para converter um número hexadecimal em uma expressão decimal, precisamos decompor o número em suas multiplicações de base, como fizemos na notação decimal, mas alterando a base para 16 . A seguir, multiplicaremos cada dígito por dezesseis elevado à posição que esse dígito específico ocupa menos um.
notação octal
O último sistema sobre o qual falaremos é a notação octal , que tem base 8. Isso significa que usa apenas oito símbolos ou números: 0, 1, 2, 3, 4, 5, 6 e 7. é o menos usado sistema de numeração de todos os que explicamos. Ressalta-se que as conversões desta notação são realizadas seguindo o mesmo procedimento das anteriores.
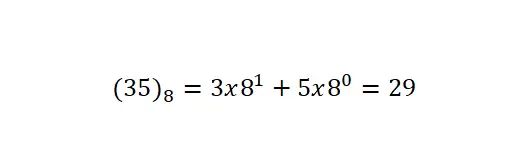
notação nova
Por fim, podemos falar do sistema de numeração romana , que hoje não é muito utilizado, mas no passado foi muito importante no campo da matemática. Pois foi uma das notações que deu vida à matemática.
Sua escrita está limitada a 7 símbolos: I (1), V (5), X (10), L (50), C (100), D (500) e M (1000). E combinando essas letras, todos os números são escritos. Se você quiser saber como eles se combinam para dar origem a outros números maiores, recomendamos a leitura do nosso artigo sobre eles, acessando pelo último link.
Como melhorar o desempenho de leitura em notação matemática?
Existem várias maneiras de melhorar o desempenho na leitura de notação matemática. Uma maneira é ler os símbolos e números em voz alta. Outra forma é familiarizar-se com os símbolos e seu significado. Você também pode praticar a leitura de notação matemática usando exercícios e problemas.
Esperamos ter ajudado você com este guia, por favor, se você tiver alguma dúvida, não hesite em escrevê-la nos comentários . Ou se você quiser dar uma contribuição sobre o tema, esperamos ver isso também nos comentários. Dito isto, deixamos para vocês um artigo sobre como aprender matemática , caso queira continuar lendo.