Multiplicação de um número por uma matriz

Nesta página veremos como multiplicar um número por uma matriz. Você também tem exemplos que o ajudarão a entendê-lo perfeitamente e exercícios resolvidos para que você possa praticar. Você também encontrará todas as propriedades do produto de um escalar e de uma matriz.

Como multiplicar um número por uma matriz?

Para multiplicar um número por uma matriz , multiplique cada elemento da matriz pelo número.

Exemplo:

Problemas resolvidos de multiplicação de um número por uma matriz

Exercício 1:

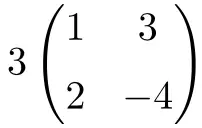
Exercício resolvido do produto de um número por uma matriz 2x2, operações com matrizes

veja solução

É uma multiplicação de um escalar por uma matriz quadrada de ordem 2:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

Exercício 2:

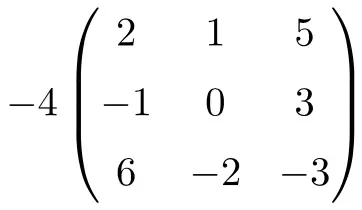
exercício resolvido passo a passo de multiplicação de um número por uma matriz 3x3, operações com matrizes

veja solução

É o produto de um número por uma matriz quadrada de ordem 3:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

Exercício 3:

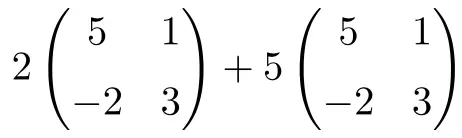
Exercício resolvido de multiplicação de um número por uma matriz 2x2, operações combinadas com matrizes

veja solução

É uma operação que combina produtos de números por matrizes e somas de matrizes de dimensão 2×2:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

Portanto, primeiro precisamos resolver os produtos:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

E finalmente adicionamos as matrizes resultantes:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

Exercício 4:

Considere as seguintes matrizes:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

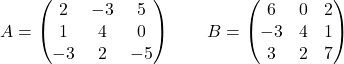
Calcular:

$\displaystyle -2A+5I-3B$

veja solução

É uma operação que combina multiplicações escalares com adições e subtrações de matrizes de dimensão 3×3. Além disso, a matriz

$I$

é a matriz identidade, que é composta por 1 na diagonal principal e 0 nos demais elementos:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

Portanto, primeiro realizamos as multiplicações:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Adicionamos as duas primeiras matrizes:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Por fim, realizamos a subtração das matrizes:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

Se estes exercícios sobre produtos escalares de matrizes foram úteis para você, não hesite em praticar com os exercícios resolvidos passo a passo sobre a adição de matrizes e o produto de matrizes , os dois tipos de operações matriciais que se repetem mais.

Propriedades do produto de um número por uma matriz

Como você bem sabe, existem muitos tipos de matrizes : matrizes quadradas, matrizes triangulares, matriz identidade, etc. Mas, felizmente, todas as propriedades do produto de números por matrizes são válidas para todas as classes de matrizes.

Aqui estão as propriedades de multiplicação entre escalares e matrizes:

Propriedade associativa:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

Observe as duas operações a seguir porque elas fornecem o mesmo resultado, não importa como multiplicamos 2 e 3:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

Propriedade distributiva em relação à adição de escalares:

$(a+b) \cdot A = a \cdot A+ b \cdot A$

Como você pode ver no exemplo abaixo, é o mesmo se primeiro adicionarmos 1+2 e depois multiplicarmos por uma matriz, ou se multiplicarmos a matriz separadamente por 1 e por 2 e depois adicionarmos os resultados:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

Propriedade distributiva em relação à adição de matrizes:

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

Em outras palavras, somar duas matrizes matemáticas e depois multiplicá-las por um número equivale a multiplicar separadamente as duas matrizes pelo mesmo número e depois somar os resultados. No exemplo abaixo você pode verificar:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

Propriedade do elemento neutro:

$1 \cdot A = A$

Portanto, ao multiplicar uma matriz por 1, não modificamos a matriz:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

Essas são todas as propriedades do produto de um escalar e de uma matriz, então esse é o fim deste artigo. Esperamos que tenha gostado e, acima de tudo, que tenha aprendido a resolver a multiplicação de números com matrizes.

Por outro lado, outras operações matriciais ligadas à multiplicação, e que são muito úteis, são potências. Deixamos aqui a página onde você aprenderá o que é e como resolver a potência de uma matriz , caso tenha curiosidade.

Multiplicando um número por uma matriz

Como multiplicar um número por uma matriz?

Exemplo:

Problemas resolvidos de multiplicação de um número por uma matriz

Exercício 1:

Exercício 2:

Exercício 3:

Exercício 4:

Propriedades do produto de um número por uma matriz

Deixe um comentário Cancelar resposta