▷ Como multiplicar polinômios (exercícios resolvidos)

Nesta página você aprenderá como os polinômios são multiplicados. Você também poderá ver exemplos de multiplicação de polinômios e, além disso, exercícios resolvidos passo a passo. Finalmente, você descobrirá quais são as propriedades da multiplicação de polinômios.

Porém, para entender completamente o conceito de multiplicação de polinômios, passaremos do mais básico ao mais complicado, ou seja, começaremos explicando como multiplicar um polinômio por um número, e depois veremos como multiplicar um polinômio por um monômio e, por fim, explicaremos como multiplicar dois ou mais polinômios entre si.

Aconselho você a seguir esta ordem, mas se você acha que já domina as operações com os polinômios anteriores pode ir diretamente para a multiplicação entre polinômios clicando no índice:

Multiplique um polinômio por um número

O produto de um escalar (ou número) e um polinômio é bastante simples de resolver, basta multiplicar o número pelo coeficiente de cada termo do polinômio .

multiplicação de um número por um polinômio

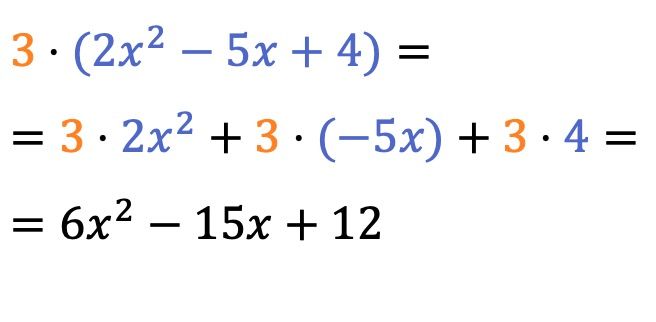
O sinal de multiplicação antes dos parênteses pode ser omitido.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

Multiplicando um polinômio por um monômio

Antes de ver como multiplicar um polinômio por um monômio, vamos primeiro lembrar como os monômios se multiplicam, pois você precisa saber disso para poder fazer esse tipo de operação polinomial.

O produto de dois monômios consiste em multiplicar seus coeficientes entre si e suas partes literais entre si, ou seja, multiplicam-se os coeficientes dos monômios e somam-se os expoentes das variáveis que possuem a mesma base. Veja o exemplo a seguir:

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

Agora vamos ver como multiplicar um monômio por um polinômio:

Em matemática, para resolver a multiplicação de um monômio por um polinômio, o monômio é multiplicado por cada termo do polinômio.

multiplicação de um polinômio por um monômio

Como antes, o sinal de multiplicação também pode ser omitido:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Observe no exemplo anterior que ao multiplicar monômios ou polinômios você também deve levar em consideração a regra dos sinais. Na verdade, um erro muito comum ao multiplicar monômios e polinômios é errar o sinal de um termo.

Certamente em algum momento, ao ver algo novo na matemática, você se perguntou: para que serve ? Pois bem, este tipo de multiplicação é utilizado para obter o fator comum de um polinômio , operação que permite simplificar polinômios (muito útil). Você pode ver o que é e como o fator comum de um polinômio é calculado neste link.

Multiplicação de dois polinômios

Depois de sabermos como multiplicar polinômios por números e por monômios, vamos ver o que é e como multiplicar polinômios por polinômios.

Para multiplicar polinômios, siga estas etapas:

Multiplique cada termo do primeiro polinômio por todos os termos do segundo polinômio.
Adicione (ou subtraia) monômios do mesmo grau (monômios semelhantes).

Para que você possa ver exatamente o que é esse método, resolveremos passo a passo a seguinte multiplicação de polinômios:

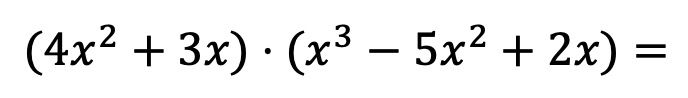
Em primeiro lugar, devemos multiplicar cada elemento do primeiro polinômio multiplicador por cada termo do segundo polinômio:

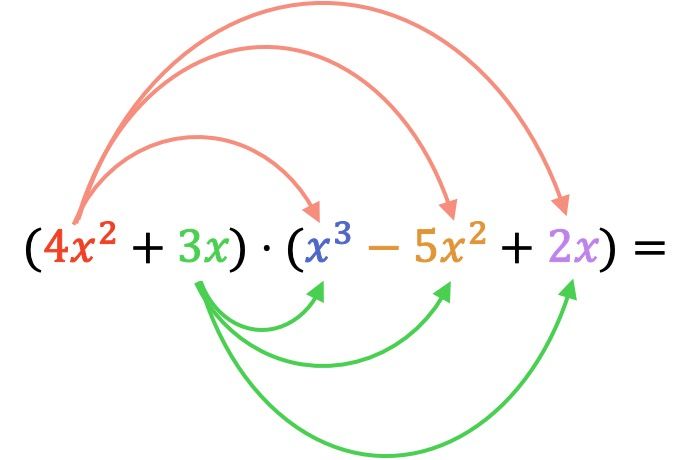
multiplicação de polinômios passo a passo

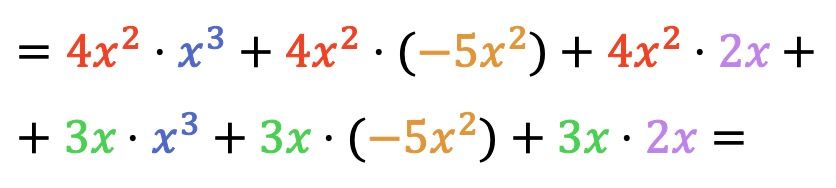
Agora fazemos todas as multiplicações de monômios:

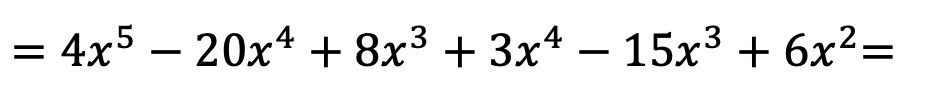
Depois de multiplicarmos os polinômios, basta agrupar os termos resultantes que são semelhantes, ou seja, os termos que têm a mesma letra e o mesmo expoente:

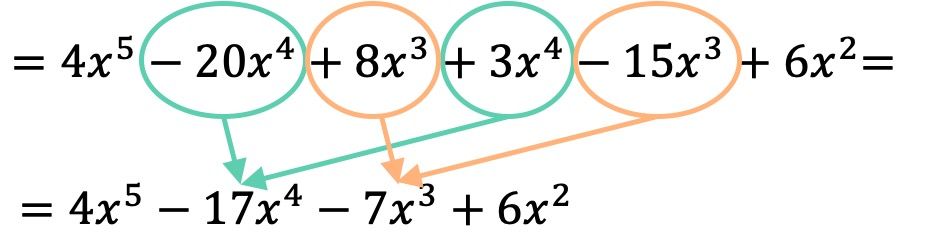
multiplicação de polinômios por polinômios

O resultado da multiplicação polinomial é, portanto:

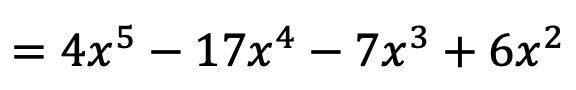
E desta forma já calculamos a multiplicação de polinômios. Talvez pareça muito difícil para você agora, mas você verá que ao praticar com dois ou três exercícios será muito mais fácil.

Agora que você viu como se resolve a multiplicação entre dois polinômios, provavelmente está interessado em saber como dividir polinômios . Na verdade, dividir polinômios é muito mais complicado do que multiplicá-los, por isso explicamos o procedimento (e dicas😉) passo a passo para que você possa entendê-lo completamente. Se você estiver interessado, clique neste link para ver como os polinômios são divididos.

Multiplicação polinomial vertical

Acabamos de ver como multiplicar um polinômio por outro polinômio horizontalmente, mas isso também pode ser feito de uma forma mais clássica: multiplicar polinômios verticalmente. Vamos ver como esse método é usado resolvendo um exemplo de multiplicação polinomial.

Se quisermos multiplicar verticalmente os dois polinômios a seguir:

$(5x^2+3x-4) \cdot (2x^2-x)$

A primeira coisa que precisamos fazer é colocar um polinômio abaixo do outro, como uma multiplicação algébrica de polinômios:

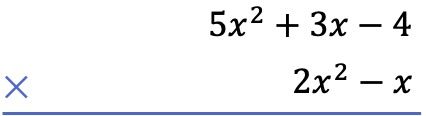
Segundo, multiplicamos cada termo do polinômio abaixo por cada termo do polinômio acima e colocamos os resultados ordenados por colunas do grau mais alto ao grau mais baixo:

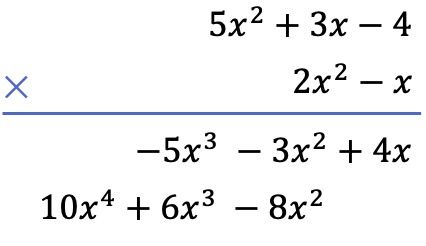
E por fim, adicionamos os termos alinhados verticalmente:

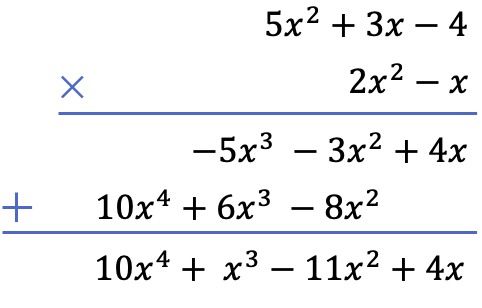
Agora que você viu os 2 métodos que existem para resolver uma multiplicação de polinômios, você sabia que também pode multiplicar frações por polinômios ? E não apenas multiplicações, mas todos os tipos de operações podem ser realizadas com esses tipos de frações. Clique neste link e descubra o que são frações algébricas .

Propriedades da multiplicação polinomial

A multiplicação de polinômios possui as seguintes características:

Propriedade comutativa : a ordem dos polinômios multiplicadores não modifica o resultado da multiplicação.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

Propriedade associativa : Quando três ou mais polinômios são multiplicados, o resultado do produto é o mesmo independente de como os fatores estão agrupados:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Propriedade distributiva : a soma de dois polinômios multiplicada por um terço é igual à soma de cada adição multiplicada pelo terceiro polinômio.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

O grau do polinômio resultante de uma multiplicação entre dois polinômios é igual à soma dos graus dos dois polinômios multiplicados.

Exercícios resolvidos sobre multiplicação de polinômios

Para que vocês possam praticar, deixo-vos com vários exercícios resolvidos sobre multiplicação de polinômios. Você pode tentar resolvê-los sozinho e verificar seus resultados com a solução proposta. Você pode então nos fazer todas as suas perguntas nos comentários, teremos o maior prazer em ajudá-lo.

Exercício 1

Calcule os seguintes produtos entre polinômios e escalares:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

Veja a solução

Para calcular a multiplicação de um polinômio por um número, deve-se multiplicar o número pelo coeficiente de cada elemento do polinômio. ENTÃO:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Exercício 2

Resolva as seguintes multiplicações entre polinômios e monômios:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

Veja a solução

Para resolver a multiplicação de um polinômio por um monômio, você deve multiplicar o referido monômio por cada termo do polinômio. ENTÃO:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Exercício 3

Determine o resultado das seguintes multiplicações entre polinômios:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

Veja a solução

Para calcular uma multiplicação de dois polinômios, precisamos multiplicar cada elemento do primeiro polinômio por cada elemento do segundo polinômio e depois agrupar termos semelhantes. ENTÃO:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Exercício 4

Encontre o resultado das seguintes multiplicações entre polinômios:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

Veja a solução

Para calcular uma multiplicação de dois polinômios, precisamos multiplicar cada elemento do primeiro polinômio por cada elemento do segundo polinômio e, em seguida, adicionar os termos semelhantes. ENTÃO:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Exercício 5

Calcule as seguintes multiplicações de polinômios:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

Veja a solução

Para fazer um produto de 2 polinômios, você deve multiplicar cada termo do primeiro polinômio por cada termo do segundo polinômio e depois agrupar os monômios semelhantes obtidos. Ainda:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Exercício 6

Resolva a seguinte multiplicação de 3 polinômios:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

Veja a solução

O funcionamento do problema consiste em 2 multiplicações de polinômios, mais precisamente é composto por dois binômios e um trinômio. Portanto, precisamos primeiro resolver um produto e depois multiplicar o resultado pelo polinômio restante.

Portanto, calculamos a primeira multiplicação:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

E agora resolvemos a multiplicação restante:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Exercício 7

Multiplique os seguintes polinômios por coeficientes racionais (com frações):

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

Veja a solução

Embora os polinômios tenham frações, ainda é uma multiplicação entre dois polinômios. Deve, portanto, ser resolvido como qualquer produto polinomial: multiplique todos os elementos e agrupe monômios semelhantes.

Portanto, multiplicamos os polinômios:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

E, por fim, somamos (ou subtraímos) os termos cujas partes literais são idênticas:

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

Para concluir este exercício com êxito, era importante que você dominasse as operações com frações. Mas se você tiver alguma dúvida sobre alguma etapa, pode perguntar nos comentários e nós responderemos o mais rápido possível.

Multiplicação (ou produto) de polinômios

Multiplique um polinômio por um número

Multiplicando um polinômio por um monômio

Multiplicação de dois polinômios

Multiplicação polinomial vertical

Propriedades da multiplicação polinomial

Exercícios resolvidos sobre multiplicação de polinômios

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Exercício 7

Deixe um comentário Cancelar resposta