Multiplicação da matriz

Nesta página veremos como multiplicar matrizes de dimensões 2×2, 3×3, 4×4, etc. Explicamos passo a passo o procedimento de multiplicação de matrizes através de um exemplo, a seguir você encontrará exercícios resolvidos para que também possa praticar. Finalmente, você aprenderá quando duas matrizes não podem ser multiplicadas e todas as propriedades desta operação matricial.

Como multiplicar duas matrizes?

Vejamos o procedimento para realizar a multiplicação de duas matrizes com um exemplo:

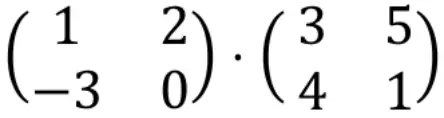
exemplo de como multiplicar duas matrizes de dimensão 2x2, operações com matrizes

Para calcular uma multiplicação de matrizes, as linhas da matriz esquerda devem ser multiplicadas pelas colunas da matriz direita.

Então, primeiro precisamos multiplicar a primeira linha pela primeira coluna. Para fazer isso, multiplicamos cada elemento da primeira linha por cada elemento da primeira coluna, um por um, e somamos os resultados. Então tudo isso será o primeiro elemento da primeira linha do array resultante. Veja o procedimento:

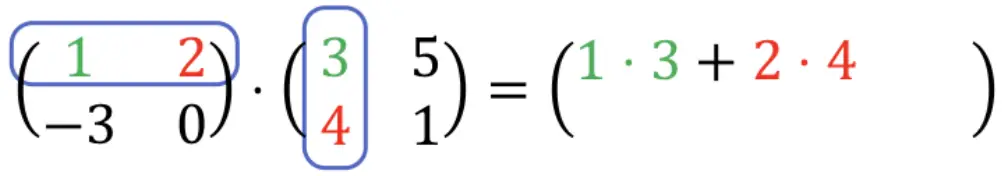
como resolver multiplicação de matrizes 2x2, operações com matrizes

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Então:

Agora precisamos multiplicar a primeira linha pela segunda coluna . Repetimos, portanto, o procedimento: multiplicamos cada elemento da primeira linha um por um por cada elemento da segunda coluna e somamos os resultados. E tudo isso será o segundo elemento da primeira linha do array resultante:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Então:

Depois de preencher a primeira linha da matriz resultante, passamos para a segunda linha. Multiplicamos, portanto , a segunda linha pela primeira coluna , repetindo o procedimento: multiplicamos um por um cada elemento da segunda linha por cada elemento da primeira coluna e somamos os resultados:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Ainda:

Finalmente, multiplicamos a segunda linha pela segunda coluna . Sempre com o mesmo procedimento: multiplicamos cada elemento da segunda linha um por um por cada elemento da segunda coluna e somamos os resultados:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Ainda:

E aqui termina a multiplicação das duas matrizes. Como você viu, é necessário multiplicar as linhas pelas colunas, repetindo sempre o mesmo procedimento: multiplicar cada elemento da linha por cada elemento da coluna um por um, e somar os resultados.

Exercícios resolvidos de multiplicação de matrizes

Exercício 1

Resolva o seguinte produto matricial:

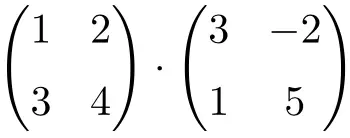
exercício resolvido produto passo a passo de matrizes 2x2, operações com matrizes

É um produto de matrizes de ordem 2:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}

Para resolver um produto matricial, você deve multiplicar as linhas da matriz esquerda pelas colunas da matriz direita.

Então primeiro multiplicamos a primeira linha pela primeira coluna. Para fazer isso, multiplicamos cada elemento da primeira linha por cada elemento da primeira coluna, um por um, e somamos os resultados. E tudo isso será o primeiro elemento da primeira linha do array resultante:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}

Agora vamos multiplicar a primeira linha pela segunda coluna, para obter o segundo elemento da primeira linha da matriz resultante:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}

Vamos para a segunda linha, então multiplicamos a segunda linha pela primeira coluna:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}

Por fim, multiplicamos a segunda linha pela segunda coluna , para calcular o último elemento da tabela:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}

Portanto, o resultado da multiplicação de matrizes é:

\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}

Exercício 2

Encontre o resultado da seguinte multiplicação de matriz quadrada 2×2:

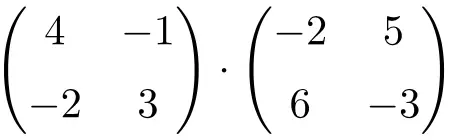
Exercício resolvido passo a passo em multiplicação de matrizes 2x2, operações matriciais

É um produto de matrizes de dimensão 2×2.

Para resolver a multiplicação, você deve multiplicar as linhas da matriz esquerda pelas colunas da matriz direita:

\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}

Exercício 3

Calcule a seguinte multiplicação de matrizes 3×3:

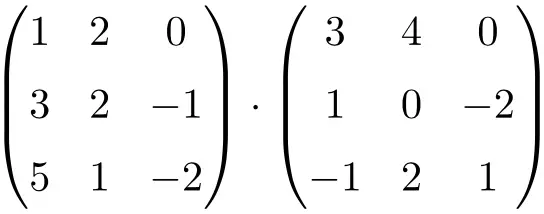
exercício resolvido multiplicação passo a passo de matrizes 3x3, operações matriciais

Para realizar a multiplicação de matrizes 3×3, você deve multiplicar as linhas da matriz esquerda pelas colunas da matriz direita:

\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}

Exercício 4

dada a matriz

A

:

\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}

Calcular:

\displaystyle 2A\cdot A^t

Vamos primeiro calcular a matriz transposta de

A

para fazer a multiplicação. E para fazer a matriz de transposição, precisamos transformar as linhas em colunas. Ou seja, a primeira linha da matriz torna-se a primeira coluna da matriz e a segunda linha da matriz torna-se a segunda coluna da matriz. Ainda:

\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

A operação matricial, portanto, permanece:

\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

Agora podemos fazer os cálculos. Primeiro calculamos

2A

(embora também possamos primeiro calcular

A \cdot A^t

):

\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =

\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

E, finalmente, resolvemos o produto das matrizes:

\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =

\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}

Exercício 5

Considere as seguintes matrizes:

\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}

Calcular:

\displaystyle A\cdot B - B \cdot A

É uma operação que combina subtração com multiplicações de matrizes de ordem 2:

\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}

Primeiro calculamos a multiplicação à esquerda:

\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =

\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}

Agora resolvemos a multiplicação à direita:

\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =

\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}

E finalmente subtraímos as matrizes:

\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =

\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}

Quando você não pode multiplicar duas matrizes?

Nem todas as matrizes podem ser multiplicadas. Para multiplicar duas matrizes, o número de colunas da primeira matriz deve corresponder ao número de linhas da segunda matriz.

Por exemplo, a seguinte multiplicação não pode ser realizada porque a primeira matriz possui 3 colunas e a segunda matriz possui 2 linhas:

\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}

Mas se invertermos a ordem, eles podem ser multiplicados. Porque a primeira matriz possui duas colunas e a segunda matriz possui duas linhas:

\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}

Propriedades de multiplicação de matrizes

Este tipo de operação matricial possui as seguintes características:

  • A multiplicação de matrizes é associativa:

\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)

  • A multiplicação de matrizes também tem a propriedade distributiva:

\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C

  • O produto de matrizes não é comutativo:

\displaystyle A \cdot B \neq B \cdot A

Por exemplo, a seguinte multiplicação de matrizes dá um resultado:

\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}

Mas o resultado do produto é diferente se invertermos a ordem de multiplicação das matrizes:

\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}

  • Além disso, qualquer matriz multiplicada pela matriz identidade resulta na mesma matriz. Isso é chamado de propriedade de identidade multiplicativa:

\displaystyle A \cdot I=A

\displaystyle I \cdot A=A

Por exemplo:

\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}

  • Finalmente, como você já deve imaginar, qualquer matriz multiplicada pela matriz zero é igual à matriz zero. Isso é chamado de propriedade multiplicativa de zero:

\displaystyle A \cdot 0=0

\displaystyle 0\cdot A=0

Por exemplo:

\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima