Aqui você encontrará a explicação do que são monômios semelhantes. Além disso, você poderá ver exemplos de monômios semelhantes e até praticar com exercícios resolvidos desse tipo de monômios.
O que são monômios semelhantes?
Obviamente, para entender o significado de monômios semelhantes, primeiro você precisa saber o que é um monômio . Portanto, recomendo que você dê uma olhada na página vinculada antes de continuar.
Então, que dois monômios são semelhantes significa o seguinte:
Monômios semelhantes são monômios que possuem exatamente a mesma parte literal. Em outras palavras, dois ou mais monômios são semelhantes quando são compostos pelas mesmas variáveis (letras) e pelos mesmos expoentes.
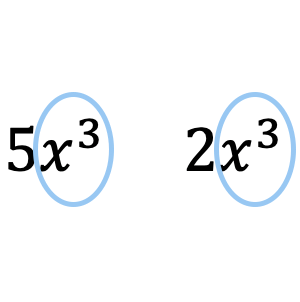
Como você pode ver no exemplo acima, o monômio
![]()
é semelhante ao monômio
![]()
porque ambos têm a mesma parte literal
![]()
mesmo que seus coeficientes sejam diferentes.
Uma das características dos monômios semelhantes é que eles são usados tanto para adicionar quanto para subtrair monômios , duas operações que você deve dominar sim ou sim. Clique em um dos dois links para ver como adicionar ou subtrair monômios. Além disso, em cada link você encontrará exemplos e exercícios resolvidos passo a passo.
Na verdade, você só pode adicionar e subtrair monômios se eles forem semelhantes. E é precisamente por isso que monômios semelhantes são tão importantes na matemática.
Exemplos de monômios semelhantes
Para que você possa entender completamente o conceito de monômios semelhantes, abaixo você pode ver vários exemplos de monômios semelhantes entre si.
Exemplo 1
![]()
Os 2 monômios anteriores são semelhantes porque suas partes literais são equivalentes
![]()
Exemplo 2
![]()
Os três monômios anteriores são semelhantes porque suas partes literais são iguais
![]()
Exemplo 3
![]()
![]()
Os quatro monômios anteriores são semelhantes entre si porque suas partes literais são idênticas
![]()
Exercício resolvido de monômios semelhantes
Combine pares de monômios que parecem semelhantes:
![Rendered by QuickLaTeX.com \begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ca52625823eec990ff41ecd05d5c1149_l3.png)
Monômios semelhantes são aqueles que possuem as mesmas partes literais. Portanto, pares de monômios semelhantes são:
![]()
![]()
![]()
![]()
Embora signifique algo completamente diferente, se você chegou até aqui, provavelmente também está interessado em saber o que é a decomposição polinomial de um número . Pois isso é algo que poucas pessoas conhecem, mas na verdade é muito útil para simplificar expressões matemáticas.