Matriz triangular superior e inferior

Nesta página você verá o que é uma matriz triangular e os diferentes tipos de matrizes triangulares junto com exemplos. Além disso, você descobrirá como calcular o determinante de uma matriz triangular e quais são as propriedades dessa matriz muito interessante. Por fim, explicamos também o que é uma matriz de Hessenberg, pois é uma matriz relacionada a matrizes triangulares.

O que é uma matriz triangular?

Definição de matriz triangular:

Uma matriz triangular é uma matriz quadrada em que todos os elementos acima ou abaixo da diagonal principal são zero (0).

Matrizes triangulares são muito utilizadas em cálculos de álgebra linear, pois inverter uma matriz triangular, calcular seu determinante, ou mesmo resolver sistemas de equações lineares com este tipo de matrizes é muito mais fácil do que com matrizes que possuem elementos diferentes de 0 em todas as posições. .

matriz triangular superior

Uma matriz triangular superior é uma matriz quadrada cujos elementos abaixo da diagonal principal são zero (0).

Exemplo de matriz triangular superior:

matriz triangular inferior

Uma matriz triangular inferior é uma matriz quadrada que possui um zero (0) em cada elemento que está acima da diagonal principal.

Exemplo de uma matriz triangular inferior:

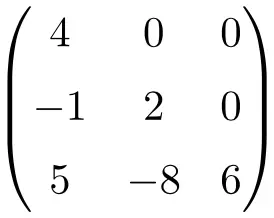
Às vezes, essas matrizes também são chamadas pela letra U, para a matriz triangular superior, e pela letra L, para a matriz triangular inferior. Embora esta nomenclatura seja usada principalmente em inglês, na verdade o U significa matriz triangular superior e o L significa matriz triangular inferior .

Exemplos de matrizes triangulares

Matriz triangular 2 × 2 dimensões

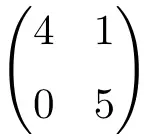
Exemplo de matriz triangular superior 2x2

Matriz triangular de ordem 3×3

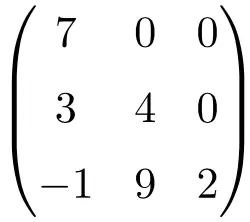
Exemplo de matriz triangular inferior 3x3

matriz triangular de tamanho 4×4

Exemplo de matriz triangular superior 4x4

Determinante de uma matriz triangular

O determinante de uma matriz triangular , seja ela triangular superior ou inferior, é o produto dos elementos da diagonal principal.

Dê uma olhada no seguinte exercício resolvido como basta calcular a multiplicação dos elementos da diagonal principal da matriz triangular para encontrar seu determinante:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Este teorema é facilmente demonstrado: basta calcular o determinante de uma matriz triangular por blocos (ou cofatores). Esta demonstração é detalhada abaixo usando uma matriz triangular genérica:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Por outro lado, sabemos que uma matriz é invertível se o seu determinante for diferente de 0. Assim, se nenhum elemento da diagonal principal for 0, a matriz triangular também será invertível e, consequentemente, será regular. matriz.

Propriedades da matriz triangular

Agora vamos ver quais são as propriedades das matrizes triangulares:

O produto de duas matrizes triangulares superiores é igual a uma matriz triangular superior. E vice-versa: multiplicar duas matrizes triangulares inferiores dá outra matriz triangular inferior.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

A transposta de uma matriz triangular superior é uma matriz triangular inferior e vice-versa: a transposta de uma matriz triangular inferior é uma matriz triangular superior.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Uma matriz triangular é invertível se todos os seus elementos da diagonal principal forem diferentes de zero, ou seja, se forem diferentes de zero. Nesse caso, a inversa de uma matriz triangular superior (inferior) também é uma matriz triangular superior (inferior).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Além disso, a diagonal principal da matriz invertida sempre conterá os inversos dos elementos da diagonal principal da matriz triangular original.

Qualquer matriz diagonal é uma matriz triangular superior e uma matriz triangular inferior, por exemplo:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Portanto, uma matriz escalar também é uma matriz triangular superior e inferior. Por exemplo, a matriz identidade:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Obviamente, a matriz zero também é uma matriz triangular superior e inferior, pois os elementos acima e abaixo da diagonal principal são 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Os autovalores (ou autovalores) de uma matriz triangular são os elementos da diagonal principal.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Uma matriz triangular superior ou inferior é sempre capaz de diagonalizar com base em autovetores (ou autovetores).

Qualquer matriz pode ser fatorada no produto de uma matriz triangular inferior e uma matriz triangular superior . Ou seja, qualquer matriz pode ser transformada em uma multiplicação de matrizes triangulares. Além disso, se a matriz for invertível, esta transformação é única. Para fatorar uma matriz, o método de decomposição LU é frequentemente usado.

Triangularizar uma matriz

Existem vários teoremas sobre matrizes que podem ser triangularizadas alterando a base. Porém, aqui veremos como triangular uma matriz aplicando transformações elementares nas retas , como no método de Gauss.

Por exemplo:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

E desta forma já triangularizamos a matriz original.

Lembre-se que as transformações elementares autorizadas entre linhas no método gaussiano são:

Substitua uma linha pela combinação linear de outras linhas.
Multiplique ou divida todos os termos consecutivos por um número diferente de 0.
Edite linhas de pedido.

Matriz de Hessenberg

A definição da matriz de Hessenberg é a seguinte:

A matriz de Hessenberg é uma matriz “quase” triangular, ou seja, todos os seus elementos são zero a partir da primeira subdiagonal (matriz de Hessenberg superior) ou da primeira superdiagonal (matriz de Hessenberg inferior).

Tenho certeza de que é melhor compreendido com um exemplo de matriz de Hessenberg superior e outro exemplo de matriz de Hessenberg inferior:

Matriz de Hessenberg superior

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Matriz inferior de Hessenberg

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Uma matriz que é uma matriz de Hessenberg superior e inferior é uma matriz tridiagonal .

Esta matriz tem o nome de Karl Hessenberg, um proeminente engenheiro e matemático alemão do século XX.

Por fim, este tipo de matriz tem a particularidade de que se for multiplicada por uma matriz triangular, o resultado é sempre uma matriz de Hessenberg.