Matriz singular ou degenerada

Nesta página você verá o que significa uma matriz ser singular ou degenerada. Além disso, mostramos vários exemplos para que você não tenha dúvidas e, por fim, explicamos todas as propriedades desse tipo de matriz.

O que é uma matriz singular ou degenerada?

A definição de uma matriz singular, também chamada de matriz degenerada, é a seguinte:

Uma matriz singular ou degenerada é uma matriz quadrada que não pode ser invertida e portanto seu determinante é igual a 0.

Assim, para saber quando uma matriz é singular, basta calcular o seu determinante: se o resultado for 0, a matriz é singular, por outro lado, se o determinante for diferente de 0, a matriz não é singular .

Se quiser saber mais sobre a matriz inversa, pode consultar esta página onde é explicado detalhadamente como inverter uma matriz usando o método Gauss , você também encontrará vários exemplos e exercícios resolvidos passo a passo para praticar.

Por outro lado, matrizes singulares também são chamadas de matrizes não regulares, porque significam exatamente o oposto de matriz regular .

Exemplos de matrizes singulares

Depois de vermos a explicação da matriz singular ou degenerada, vejamos alguns exemplos de matrizes singulares com diversas dimensões:

Exemplo de matriz singular 2×2

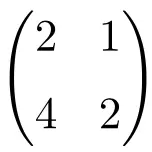
exemplo de uma matriz singular ou degenerada de dimensão 2x2

Podemos facilmente verificar que se trata de uma matriz singular calculando seu determinante:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

O determinante da matriz de ordem 2 é igual a 0, portanto é uma matriz singular.

Exemplo de matriz singular 3 × 3

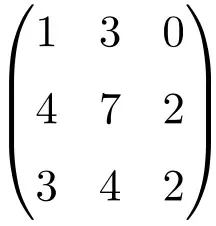
exemplo de uma matriz singular ou degenerada de dimensão 3x3

Devemos resolver o determinante da matriz para verificar que é uma matriz não invertível:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

O determinante da matriz de ordem 3 dá 0, é portanto uma matriz singular.

Exemplo de matriz singular 4 × 4

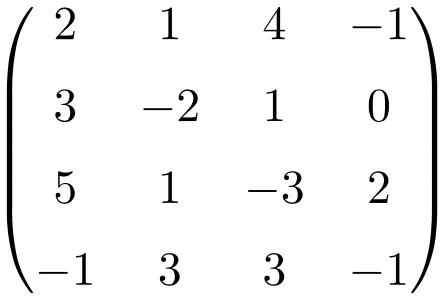
exemplo de uma matriz singular ou degenerada de dimensão 4x4

Fazendo o determinante da matriz mostramos que ela é uma matriz singular:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

O determinante da matriz de ordem 4 é zero, portanto sua matriz inversa não existe.

Atenção: Se tiver dúvidas sobre os cálculos de determinantes, pode consultar a página como calcular um determinante .

Propriedades de matrizes singulares

As características deste tipo de matrizes são as seguintes:

Pelo menos duas colunas ou duas linhas de uma matriz singular são combinações lineares e, portanto, lineares dependentes.

Qualquer matriz contendo uma linha ou coluna preenchida com zeros é uma matriz singular.

A classificação de uma matriz singular ou degenerada é menor que seu tamanho.

O produto matricial de uma matriz singular multiplicado por qualquer outra matriz dá outra matriz singular. Esta condição pode ser deduzida das propriedades dos determinantes:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Da mesma forma, a potência de uma matriz singular é igual a outra matriz singular, independentemente da potência à qual ela é elevada.

A transposta de uma matriz singular dá origem a outra matriz singular, pois o determinante de uma matriz transposta (ou transposta) é equivalente ao determinante da matriz não transposta:

$\text{det}(A^t) = \text{det}(A)=0$

Multiplicar uma matriz singular por um escalar não altera seu status de matriz degenerada.

O adjunto de uma matriz singular também é singular.

Matrizes triangulares e matrizes diagonais são matrizes degeneradas se pelo menos um elemento de sua diagonal principal for zero.

Obviamente, a matriz zero é uma matriz singular.

Da mesma forma, uma matriz nilpotente também é uma matriz singular.

Um sistema de equações lineares associado a uma matriz singular não tem solução ou tem infinitas soluções.

Por fim, uma matriz quadrada é singular se e somente se tiver pelo menos um autovalor (ou autovalor) igual a 0.