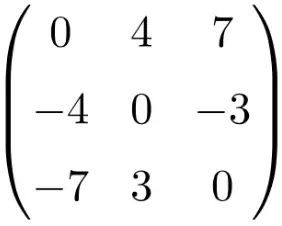Nesta página explicamos o que é uma matriz quadrada e você encontrará exemplos de matrizes quadradas. Além disso, você verá quais propriedades as matrizes quadradas possuem, as operações que podem ser feitas com elas e os diferentes tipos que existem.
O que é uma matriz quadrada?
Uma matriz quadrada é uma matriz que possui o mesmo número de linhas que colunas.
Exemplos de matrizes quadradas
matriz quadrada de ordem 2
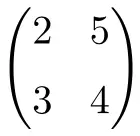
matriz quadrada de ordem 3
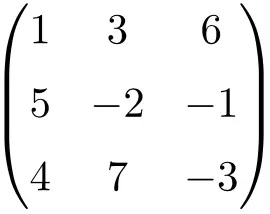
matriz quadrada de ordem 4
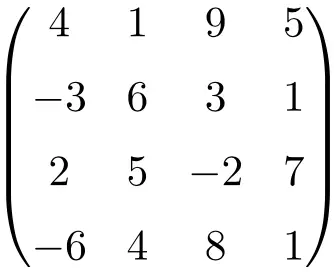
Como você pode ver, as matrizes quadradas geralmente são nomeadas pela sua ordem, ou seja, uma matriz quadrada de ordem 2 significa que é uma matriz de dimensão 2×2 (2 linhas e 2 colunas), ou falamos de uma matriz quadrada de ordem 3 o que indica que é de tamanho 3×3 (3 linhas e 3 colunas).
Diagonais de uma matriz quadrada
As diagonais das matrizes quadradas possuem nomes particulares, existe a diagonal principal e a diagonal secundária:
- A diagonal principal de uma matriz quadrada consiste nos elementos que vão do canto superior esquerdo ao canto inferior direito:

- A diagonal secundária de uma matriz quadrada corresponde aos elementos que vão do canto inferior esquerdo ao canto superior direito:

Propriedades de uma matriz quadrada
Matrizes quadradas são amplamente utilizadas em álgebra linear, por isso são tão importantes. Então vamos ver quais são as características que tornam esta classe de matrizes tão relevante:
- Qualquer matriz quadrada pode ser decomposta na soma de uma matriz simétrica e de uma matriz antissimétrica .
- Se duas matrizes quadradas são da mesma ordem, elas podem ser adicionadas ou subtraídas uma da outra:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- Duas matrizes quadradas podem ser multiplicadas em ambas as direções possíveis. Porém, o produto de matrizes quadradas não é comutativo, ou seja, o resultado da multiplicação mudará dependendo de qual lado for multiplicado. Observe no exemplo a seguir como o resultado depende das posições das matrizes:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Matrizes quadradas são as únicas que podem calcular o determinante. Portanto, um determinante só pode ser resolvido se for uma matriz quadrada. Por exemplo, para encontrar o determinante de uma matriz quadrada 3×3, você deve aplicar a regra de Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Lembre-se também que se o determinante da matriz for diferente de 0, significa que se trata de uma matriz regular , ou seja, é invertível. Por outro lado, se o determinante for zero, é uma matriz singular (que não possui inversa).
- Finalmente, matrizes quadradas podem ser diagonalizadas . Assim, uma mudança de base pode ser realizada para calcular os autovalores (ou autovalores) e os autovetores (ou autovetores) de uma matriz quadrada.
Operações com matrizes quadradas
Como vimos, o determinante de uma matriz só pode ser calculado se a matriz for quadrada. Da mesma forma, também existem certas operações que só podem ser realizadas se a matriz for de dimensão quadrada:
traço de uma matriz
O traço de uma matriz é a soma dos elementos que formam a diagonal principal de uma matriz quadrada.
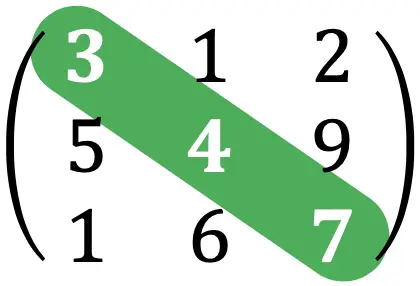
Por exemplo, o traço da matriz do exercício acima seria:
![]()
Tipos de matrizes quadradas
Então você tem os tipos mais importantes de matrizes quadradas que existem. Clique no tipo de dado para descobrir o que há de especial nele.
Como você pode ver, existem muitos tipos de matrizes quadradas e cada uma tem seu próprio nome por um motivo diferente.