Nesta página você encontrará a explicação da matriz zero, também chamada de matriz nula. Você também verá com exemplos que os valores de seus elementos são independentes da dimensão da matriz e, por fim, encontrará todas as propriedades deste tipo de matriz.
Qual é a matriz nula?
A matriz nula (ou matriz nula) é uma matriz cujos elementos são todos iguais a zero (0).
Portanto, pela definição de matriz zero, esta matriz pode ter todas as dimensões possíveis, desde que todos os seus números sejam zero. Veja os seguintes exemplos:
Exemplos de matrizes nulas
Exemplo de matriz nula 2 × 2
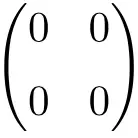
Exemplo de matriz nula 3 × 3
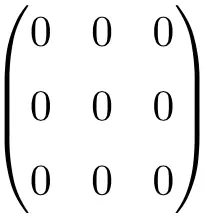
Exemplo de matriz nula 4 × 4
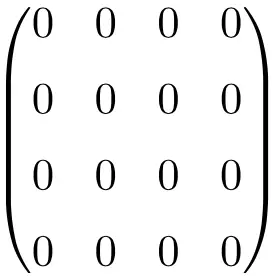
Pode agora parecer-lhe que esta matriz muito particular não importa, uma vez que é simplesmente uma matriz cheia de zeros. Porém, em matemática, mais especificamente na área de álgebra linear, é uma matriz muito útil porque facilita muito os cálculos.
Propriedades da matriz nula
Matrizes nulas (ou nulas) possuem as seguintes características:
- A matriz zero é o elemento neutro da operação de adição de matrizes, portanto:
![]()
- A multiplicação de matrizes tem a propriedade multiplicativa de zero, ou seja, o produto de qualquer matriz multiplicado pela matriz zero é igual a 0.
![]()
- Se a matriz for quadrada, a matriz zero é simétrica e antissimétrica .
- A matriz zero é a única matriz cuja classificação é zero.
- O determinante da matriz zero sempre avalia 0, portanto este tipo de matriz não possui inversa (é uma matriz singular).
- Obviamente, a matriz zero é um exemplo de matriz nilpotente .