Matriz Jacobiana e Jacobiana

Nesta página você encontrará o que é a matriz Jacobiana e como calculá-la usando um exemplo. Além disso, você tem vários exercícios resolvidos sobre matrizes Jacobianas para praticar. Você também verá por que o determinante da matriz Jacobiana, a Jacobiana, é tão importante. Por fim, explicamos as relações que esta matriz mantém com outras operações e as aplicações que possui.

Qual é a matriz Jacobiana?

A definição da matriz Jacobiana é a seguinte:

A matriz Jacobiana é uma matriz formada pelas derivadas parciais de primeira ordem de uma função.

A fórmula para a matriz Jacobiana é, portanto, a seguinte:

Portanto, as matrizes Jacobianas sempre terão tantas linhas quantas funções escalares

$(f_1,f_2,\ldots ,f_m)$

tem a função, e o número de colunas corresponderá ao número de variáveis

$(x_1, x_2, \ldots , x_n).$

Por outro lado, esta matriz também é conhecida como mapa diferencial Jacobiano ou mapa linear Jacobiano . Na verdade, às vezes também é escrito com a letra D em vez da letra J:

$\displaystyle J_f = D_f$

A título de curiosidade, a matriz Jacobiana leva o nome de Carl Gustav Jacobi, importante matemático e professor do século XIX que fez importantes contribuições para o mundo da matemática, particularmente na área da álgebra linear.

Exemplo de cálculo da matriz Jacobiana

Assim que vermos o conceito de matriz Jacobiana, veremos passo a passo como ela é calculada usando um exemplo:

Determine a matriz Jacobiana no ponto (1,2) da seguinte função:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

A primeira coisa que precisamos fazer é calcular todas as derivadas parciais de primeira ordem da função:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Agora aplicamos a fórmula da matriz Jacobiana. Neste caso, a função possui duas variáveis e duas funções escalares, portanto a matriz Jacobiana será uma matriz quadrada de dimensão 2×2:

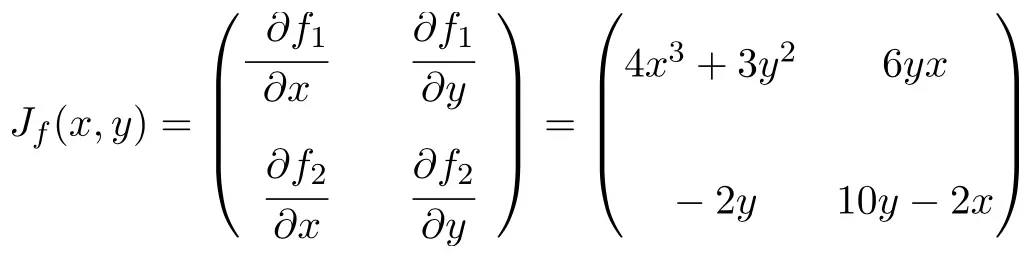
Assim que tivermos a expressão para a matriz Jacobiana, avaliamos-a no ponto (1,2):

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

E, por fim, realizamos as operações e obtemos a solução:

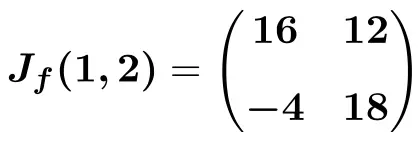
Depois de ver como encontrar a matriz Jacobiana de uma função, deixamos vários exercícios resolvidos passo a passo para que você possa praticar.

Problemas resolvidos de matrizes Jacobianas

Exercício 1

Encontre a matriz Jacobiana no ponto (0,-2) da seguinte função vetorial em 2 variáveis:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

veja solução

A função possui duas variáveis e duas funções escalares, então a matriz Jacobiana será uma matriz quadrada de tamanho 2×2:

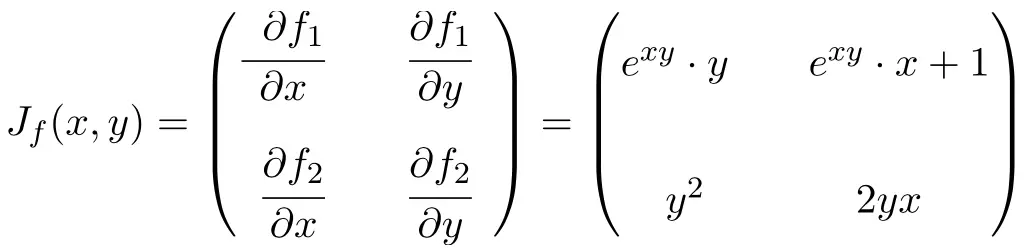
Depois de calcularmos a expressão para a matriz Jacobiana, avaliamos-a no ponto (0,-2):

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

E, por fim, realizamos as operações e obtemos o resultado:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Exercício 2

Calcule a matriz Jacobiana no ponto (2,-1) da seguinte função com 2 variáveis:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

veja solução

Neste caso, a função possui duas variáveis e duas funções escalares, portanto a matriz Jacobiana será uma matriz quadrada de ordem 2:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Assim que encontrarmos a expressão para a matriz Jacobiana, avaliamos-a no ponto (2,-1):

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

E, por fim, realizamos as operações e obtemos o resultado:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Exercício 3

Determine a matriz Jacobiana no ponto (2,-2,2) da seguinte função com 3 variáveis:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

veja solução

Neste caso, a função possui três variáveis e duas funções escalares, portanto, a matriz Jacobiana será uma matriz retangular de dimensão 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

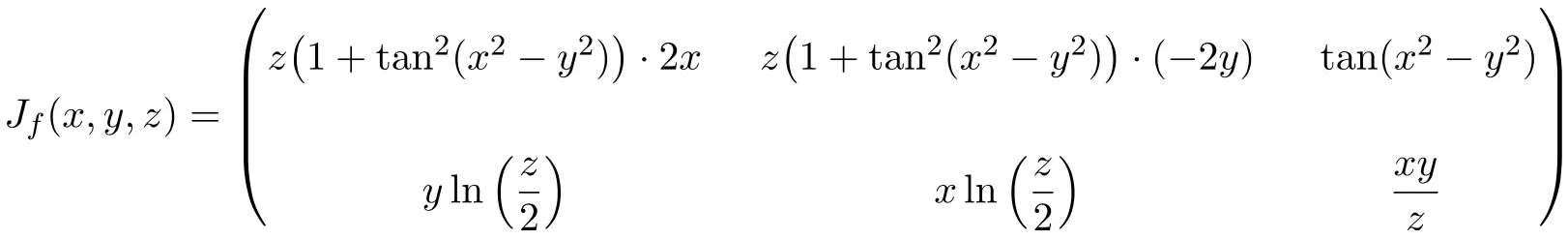
Exercício resolvido de matriz Jacobiana de 3 variáveis

Assim que tivermos a expressão para a matriz Jacobiana, avaliamos-a no ponto (2,-2,2):

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Realizamos os cálculos:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

E continuamos a operar até que não possa mais ser simplificado:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Exercício 4

Determine a matriz Jacobiana no ponto

$(\pi, \pi)$

da seguinte função multivariável:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

veja solução

Neste caso, a função possui duas variáveis e três funções escalares, portanto, a matriz Jacobiana será uma matriz retangular de dimensão 3×2:

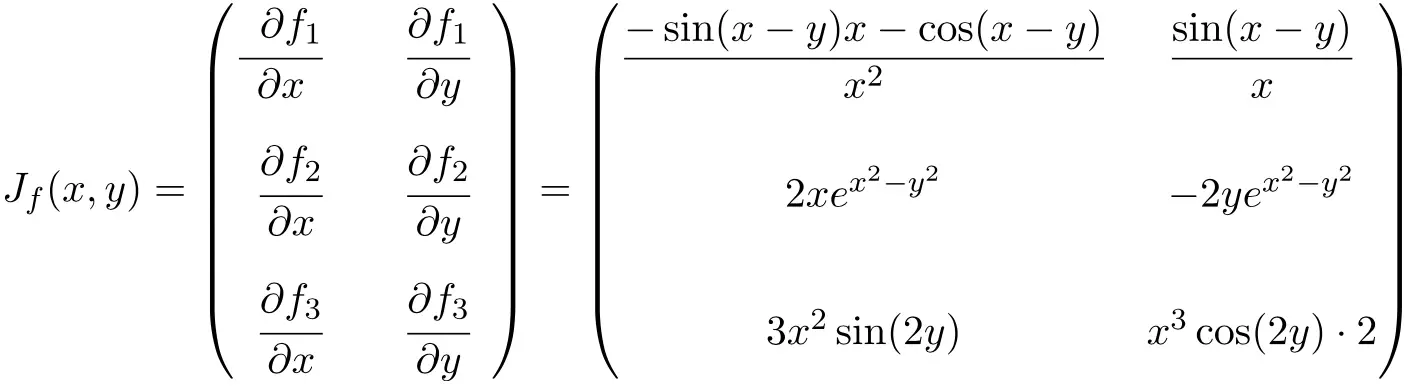
exercício resolvido passo a passo da matriz Jacobiana

Assim que tivermos a expressão para a matriz Jacobiana, nós a avaliamos até o ponto

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Realizamos as operações:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Assim a matriz Jacobiana da função vetorial no ponto considerado vale:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Exercício 5

Calcule a matriz Jacobiana no ponto

$(3,0,\pi)$

da seguinte função com 3 variáveis:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

veja solução

Neste caso, a função é de três variáveis e três funções escalares, portanto, a matriz Jacobiana será uma matriz quadrada de dimensão 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

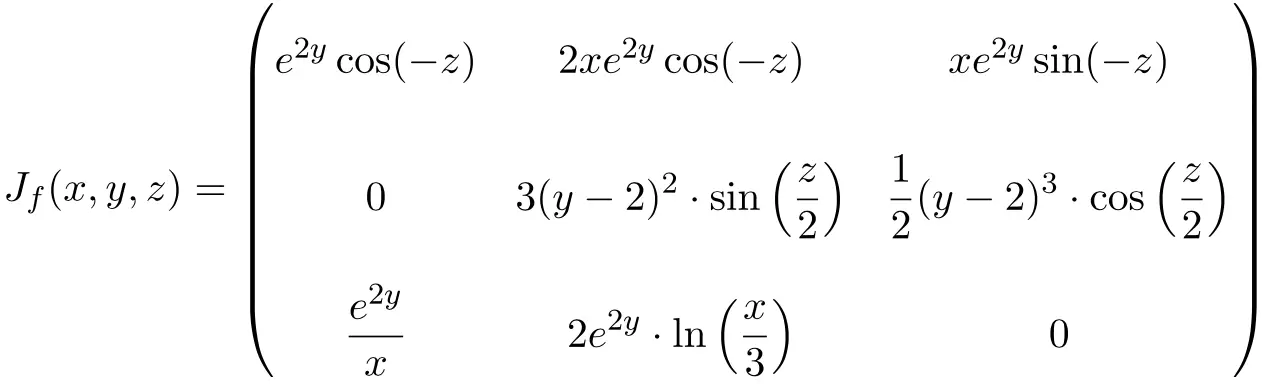
Exercício resolvido de matriz Jacobiana 3x3 com 3 variáveis

Uma vez encontrada a matriz Jacobiana, nós a avaliamos no ponto

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

Calculamos as operações:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

E o resultado da matriz Jacobiana no ponto é:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Determinante da matriz Jacobiana: a Jacobiana

O determinante da matriz Jacobiana é denominado determinante Jacobiano ou Jacobiano. Deve-se levar em consideração que a Jacobiana só pode ser calculada se a função tiver o mesmo número de variáveis que as funções escalares, pois então a matriz Jacobiana terá o mesmo número de linhas que de colunas e, portanto, será um quadrado matriz. .

Exemplo jacobiano

Vejamos um exemplo de cálculo do determinante Jacobiano de uma função com duas variáveis:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

Primeiro calculamos a matriz Jacobiana da função:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

E agora resolvemos o determinante da matriz 2×2:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

O Jacobiano e a invertibilidade de uma função

Agora que você viu o conceito do Jacobiano, provavelmente já pensou… bem, qual é o sentido?

Bem, o principal uso do Jacobiano é determinar se uma função pode ser invertida. O teorema da função inversa diz que se o determinante da matriz Jacobiana (a Jacobiana) for diferente de 0, isso significa que esta função é invertível.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Ressalta-se que esta condição é necessária mas não suficiente, ou seja, se o determinante for diferente de zero, podemos afirmar que a matriz pode ser invertida, porém, se o determinante for 0, não podemos saber se o função tem um inverso ou Não.

Por exemplo, no exemplo visto anteriormente de como encontrar o Jacobiano de uma função, o determinante dá

$4x^2+4y^2$

. Neste caso podemos afirmar que a função sempre pode ser invertida exceto no ponto (0,0), pois este ponto é o único onde o determinante Jacobiano é igual a zero e, portanto, não sabemos se a função inversa existe neste ponto.

Relação da matriz Jacobiana com outras operações

A matriz Jacobiana está relacionada ao gradiente e à matriz Hessiana de uma função:

Declive

Se a função for uma função escalar, a matriz Jacobiana será uma matriz linha que será equivalente ao gradiente :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Matriz hessiana

A matriz Jacobiana do gradiente de uma função é igual à matriz Hessiana :

$\displaystyle H_f = J(\nabla f)$

A Hessiana é uma matriz muito importante para a derivação de funções com mais de uma variável, pois é formada pelas segundas derivadas da função. Na verdade, pode-se dizer que a matriz Hessiana é a continuidade da matriz Jacobiana. Mas é tão importante que tenhamos uma página inteira que explica detalhadamente. Então se você quiser saber exatamente o que é essa matriz e por que ela é tão especial, você pode clicar no link.

Aplicações da matriz Jacobiana

Além da utilidade que vimos da Jacobiana, que determina se uma função é invertível, a matriz Jacobiana tem outras aplicações.

A matriz Jacobiana é utilizada para calcular os pontos críticos de uma função multivariada, que são então classificados em máximos, mínimos ou pontos de sela através da matriz Hessiana. Para encontrar os pontos críticos, você precisa calcular a matriz Jacobiana da função, igualá-la a 0 e resolver as equações resultantes.

$\displaystyle J_f(x)=0$

Adicionalmente, outra aplicação da matriz Jacobiana é encontrada na integração de funções com mais de uma variável, ou seja, em integrais duplas, triplas, etc. Já o determinante da matriz Jacobiana permite uma mudança de variável em integrais múltiplas de acordo com a seguinte fórmula:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Onde T é a função de mudança de variável que relaciona as variáveis originais com as novas.

Por fim, a matriz Jacobiana também é utilizada para fazer uma aproximação linear de qualquer função

$f$

em torno de um ponto

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Matriz jacobiana e jacobiana

Qual é a matriz Jacobiana?

Exemplo de cálculo da matriz Jacobiana

Problemas resolvidos de matrizes Jacobianas

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Determinante da matriz Jacobiana: a Jacobiana

Exemplo jacobiano

O Jacobiano e a invertibilidade de uma função

Relação da matriz Jacobiana com outras operações

Declive

Matriz hessiana

Aplicações da matriz Jacobiana

Deixe um comentário Cancelar resposta