Matriz Hessiana (ou Hesse) -

Esta página é certamente a explicação mais completa da matriz Hessiana que existe. Aqui é explicado o conceito de matriz Hessiana, como calculá-la com exemplos e há ainda vários exercícios resolvidos para praticar. Além disso, você poderá aprender como são calculados os valores máximo e mínimo de uma função multivariável, bem como se é uma função côncava ou convexa. E, finalmente, você também encontrará os utilitários e aplicativos da matriz Hessiana.

Qual é a matriz Hessiana?

A definição da matriz Hessiana (ou Hessiana) é a seguinte:

A matriz Hessiana é uma matriz quadrada de dimensão n × n composta pelas segundas derivadas parciais de uma função de n variáveis.

Essa matriz também é conhecida como Hessiana, ou mesmo em alguns livros de matemática é chamada de Discriminante. Mas a forma mais comum de chamá-la é a matriz Hessiana.

A fórmula para a matriz Hessiana é, portanto, a seguinte:

Portanto, a matriz Hessiana será sempre uma matriz quadrada cuja dimensão será igual ao número de variáveis da função. Por exemplo, se a função tiver 3 variáveis, a matriz Hessiana terá dimensão 3×3.

Além disso, o teorema de Schwarz (ou teorema de Clairaut) diz que a ordem de diferenciação não importa, ou seja, deriva parcialmente primeiro em relação à variável

$x_1$

então em relação à variável

$x_2$

equivale a diferenciar parcialmente em relação a

$x_2$

então respeite

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

Portanto, a matriz Hessiana é uma matriz simétrica , ou seja, possui uma simetria cujo eixo é a sua diagonal principal.

A título de curiosidade, a matriz Hessiana leva o nome de Ludwig Otto Hesse, um matemático alemão do século XIX que fez contribuições muito importantes ao campo da álgebra linear.

Exemplo de cálculo da matriz Hessiana

Vejamos um exemplo de como encontrar uma matriz Hessiana de dimensão 2 × 2:

Calcule a matriz Hessiana no ponto (1,0) da seguinte função:

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

Primeiro, precisamos calcular as derivadas parciais de primeira ordem:

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

Uma vez que já conhecemos as primeiras derivadas, calculamos todas as derivadas parciais de segunda ordem:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

Portanto, podemos agora encontrar a matriz Hessiana a partir da fórmula para matrizes 2 × 2:

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

Assim a matriz Hessiana avaliada no ponto (1,0) será:

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

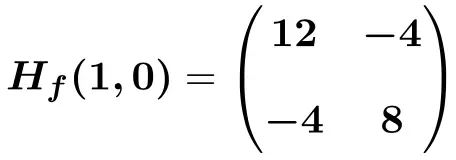
exemplos de matrizes de serapilheira ou juta

Problemas resolvidos de matrizes Hessianas

Exercício 1

Calcule a matriz Hessiana da seguinte função com 2 variáveis no ponto (1,1):

$\displaystyle f(x,y)=x^2y+y^2x$

veja solução

Primeiro, precisamos encontrar as derivadas parciais de primeira ordem da função:

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

Depois de já termos calculado as primeiras derivadas, procedemos à resolução de todas as derivadas parciais de segunda ordem:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

Assim a matriz Hessiana é definida da seguinte forma:

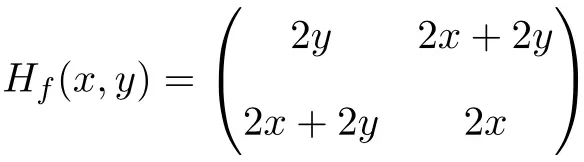
Exercício resolvido da matriz Hessiana ou Hessiana de dimensão 2x2

Finalmente, resta avaliar a matriz Hessiana no ponto (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

Exercício 2

Calcule o Hessian no ponto (1,1) da seguinte função em duas variáveis:

$\displaystyle f(x,y)= e^{y\ln x}$

veja solução

Primeiro, precisamos calcular as derivadas parciais de primeira ordem da função:

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

Assim que tivermos as primeiras derivadas, calculamos as derivadas parciais de segunda ordem da função:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

Assim, a matriz Hessiana da função é uma matriz quadrada de dimensão 2×2:

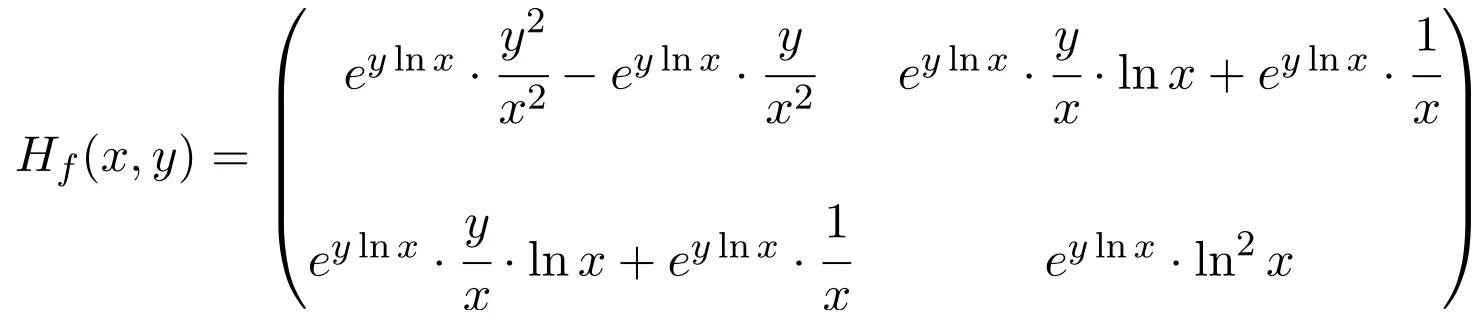
Exercício Hessiano resolvido ou matriz Hessiana de dimensão 2x2

Finalmente, resta avaliar a matriz Hessiana no ponto (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Exercício 3

Encontre a matriz Hessiana no ponto

$(0,1,\pi)$

da seguinte função com 3 variáveis:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

veja solução

Primeiro, calculamos as derivadas parciais de primeira ordem da função:

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

Assim que tivermos as primeiras derivadas, calculamos as derivadas parciais de segunda ordem da função:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

Para que a matriz Hessiana da função seja uma matriz quadrada de dimensão 3×3:

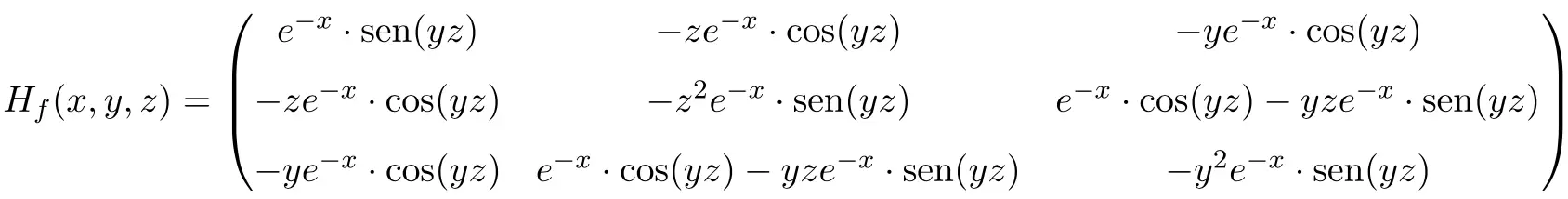
exemplo de serapilheira ou matriz de serapilheira de dimensão 3x3

Por fim, substituímos as variáveis pelos seus respectivos valores no ponto

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

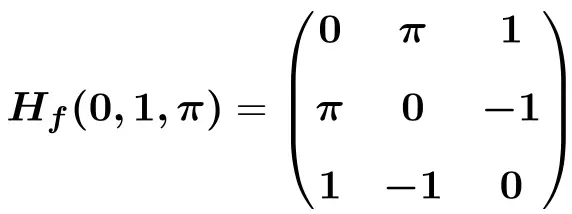
exercício resolvido passo a passo da matriz Hessiana ou Hessiana de dimensão 3x3

Exercício 4

Determine a matriz Hessiana no ponto (2,-1,1,-1) da seguinte função com 4 variáveis:

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

veja solução

O primeiro passo é encontrar as derivadas parciais de primeira ordem da função:

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

Agora resolvemos as derivadas parciais de segunda ordem da função:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

Assim, a expressão da matriz Hessiana 4×4 obtida resolvendo todas as derivadas parciais é a seguinte:

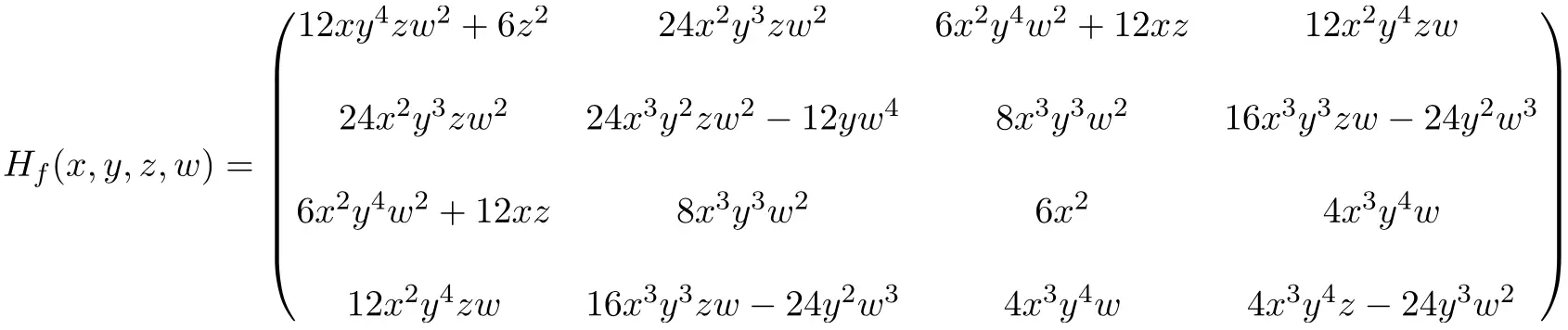
exemplo resolvido passo a passo de serapilheira ou matriz de serapilheira de dimensão 4x4

Por fim, substituímos as incógnitas pelos seus respectivos valores de pontos (2,-1,1,-1) e fazemos os cálculos:

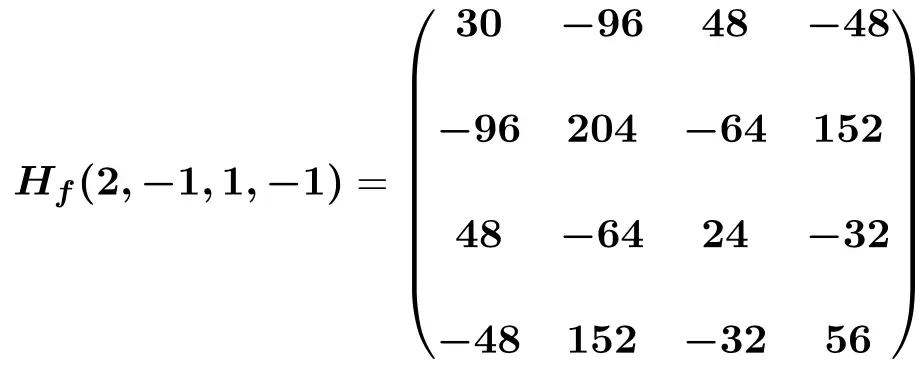
Exercício resolvido passo a passo da matriz Hessiana ou Hessiana de dimensão 4x4

Como saber quando a matriz Hessiana é positiva, negativa ou indefinida?

Como veremos mais tarde, saber se a matriz Hessiana é uma matriz positiva semidefinida, positiva definida, negativa semidefinida, negativa definida ou indefinida é muito útil. Então, vamos ver como podemos descobrir:

Critério de autovalores (ou autovalores)

Uma forma de saber que tipo de matriz é é percorrer os autovalores (ou autovalores) da matriz Hessiana:

A matriz Hessiana é positiva semidefinida se tiver autovalores (ou autovalores) iguais e maiores que zero. Ou seja, possui autovalores positivos e pelo menos um igual a 0:

$\lambda \geq 0$

A matriz Hessiana é positiva definida se todos os seus autovalores (ou autovalores) forem exclusivamente maiores que 0 (positivo):

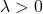$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li> A matriz Hessiana é <span style=$ negativa semidefinida se tiver autovalores (ou autovalores) iguais e menores que zero. Ou seja, possui autovalores negativos e pelo menos um igual a 0:

$\lambda \leq 0$

A matriz Hessiana é definida negativa se todos os seus autovalores (ou autovalores) forem menores que 0 (negativos):

$\lambda < 0$

A matriz Hessiana é indefinida quando possui autovalores positivos e negativos (ou autovalores):

$\lambda > 0 \qquad \lambda <0$

Critério de Sylvester

Outra forma de saber de que tipo é a matriz Hessiana é utilizar o critério de Sylvester, embora este teorema apenas nos permita saber se é definida positiva, definida negativa ou indefinida. Mas às vezes pode ser muito mais rápido de usar porque os cálculos geralmente são mais fáceis.

Assim, o critério de Sylvester é o seguinte:

Se todos os menores principais da matriz Hessiana forem maiores que 0, é uma matriz definida positiva .

Se os principais menores da matriz Hessiana com índice par forem maiores que 0 e aqueles com índice ímpar forem menores que 0, é uma matriz definida negativa .

Se todos os menores principais da matriz Hessiana forem diferentes de 0 e nenhuma das duas condições anteriores for atendida, é uma matriz indefinida .

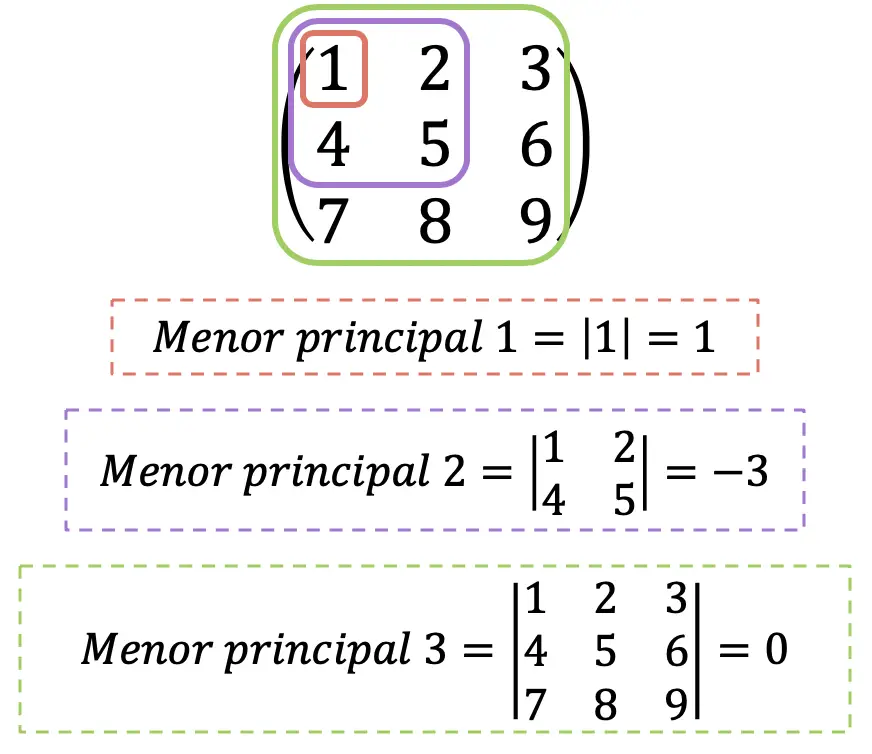
principais menores de uma matriz hessiana

Obviamente, o máximo menor principal da matriz Hessiana coincidirá sempre com o seu determinante. Apenas para fins informativos, o determinante da matriz Hessiana também é chamado de “o Hessiano”, embora não o façamos aqui para evitar confusão.

Como calcular o máximo ou mínimo de uma função com a matriz Hessiana

Depois de saber como calcular a matriz Hessiana, você provavelmente está se perguntando: e para que serve essa matriz?

Pois bem, uma das aplicações da matriz Hessiana é encontrar o máximo ou mínimo de uma função com mais de uma variável. Aqui está uma explicação passo a passo de como calcular máximos e mínimos:

Primeiro, são calculados os pontos críticos da função multivariável. Para isso, calculamos o gradiente ou a matriz Jacobiana da função, igualamos-o a 0 e resolvemos as equações.
A matriz Hessiana é calculada.
Os pontos críticos encontrados na etapa 1 são substituídos na matriz Hessiana. Obteremos assim tantas matrizes Hessianas quantos pontos críticos a função tiver.
Vemos que tipo de matriz é cada matriz Hessiana. Ou seja, procuramos ver se é definido positivo, definido negativo, indefinido, etc.
- Se a matriz Hessiana for positiva definida, o ponto crítico é um mínimo relativo da função.
- Se a matriz Hessiana for definida negativa, o ponto crítico é um máximo relativo da função.
- Se a matriz Hessiana for indefinida, o ponto crítico é um ponto de sela .

Exemplo de cálculo de máximos e mínimos de uma função multivariável

Para ver como isso é feito, aqui está um exemplo de cálculo e classificação dos extremos relativos de uma função usando a matriz Hessiana:

Encontre todos os extremos relativos da seguinte função multivariável:

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

A primeira coisa que precisamos fazer é calcular a matriz Jacobiana da função, que neste caso coincidirá com o gradiente por ser uma função escalar:

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

Devemos agora determinar os pontos críticos, para isso igualamos as equações obtidas a 0 e resolvemos o sistema de equações:

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

Portanto, o ponto crítico que encontramos é (0,-2).

Uma vez encontrado o ponto crítico da função, devemos calcular a matriz Hessiana:

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

E, obviamente, a matriz Hessiana avaliada no ponto crítico é a mesma:

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Para ver que tipo de matriz é, usaremos o critério de Sylvester. Portanto, resolvemos os principais menores da matriz:

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

O menor principal 1 (ímpar) é positivo e o menor principal 2 (par) é negativo, portanto, pelo critério de Sylvester, é uma matriz indefinida. E, portanto, o ponto crítico (0,-2) é um ponto de sela.

Determinando a concavidade ou convexidade de uma função com a matriz Hessiana

Outro uso da matriz Hessiana é saber se uma função é côncava ou convexa. E isso pode ser determinado pelo seguinte teorema:

Ser

$A \subseteq \mathbb{R}^n$

um conjunto aberto e

$f \colon A \to \mathbb{R}$

uma função cujas segundas derivadas são contínuas, sua concavidade e convexidade são definidas pela matriz Hessiana:

Função
$f$

é convexo em toda parte

$A$

se e somente se sua matriz Hessiana for positiva semidefinida em todos os pontos do conjunto.
Função
$f$

é estritamente convexo em todo

$A$

se e somente se sua matriz Hessiana for positiva definida em todos os pontos do conjunto.

✓ Portanto, se

$f$

é uma função convexa em um ponto onde a matriz Jacobiana também desaparece, este ponto é um mínimo local .

Função
$f$

é côncavo em geral

$A$

se e somente se sua matriz Hessiana for negativa semidefinida em todos os pontos do conjunto.
Função
$f$

é estritamente côncavo em geral

$A$

se e somente se sua matriz Hessiana for negativa definida em todos os pontos do conjunto.

✓ Portanto, se

$f$

é uma função côncava em um ponto onde a matriz Jacobiana também desaparece, este ponto é um máximo local .

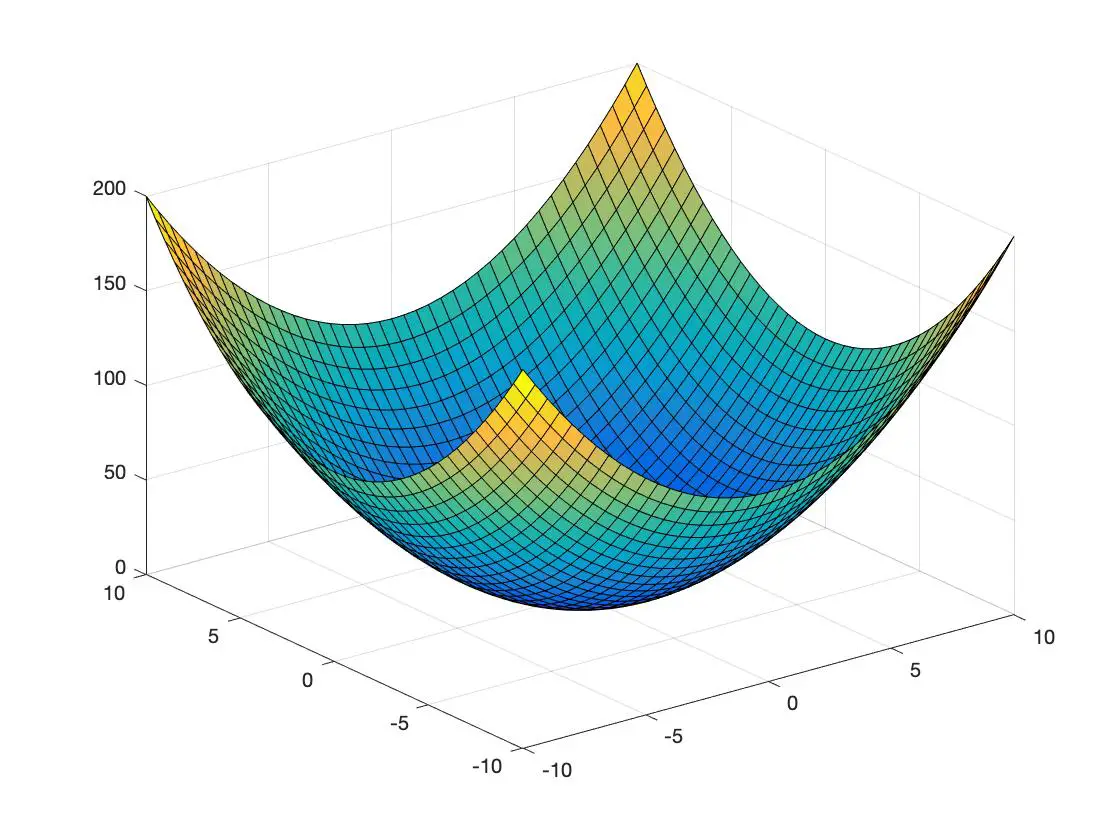
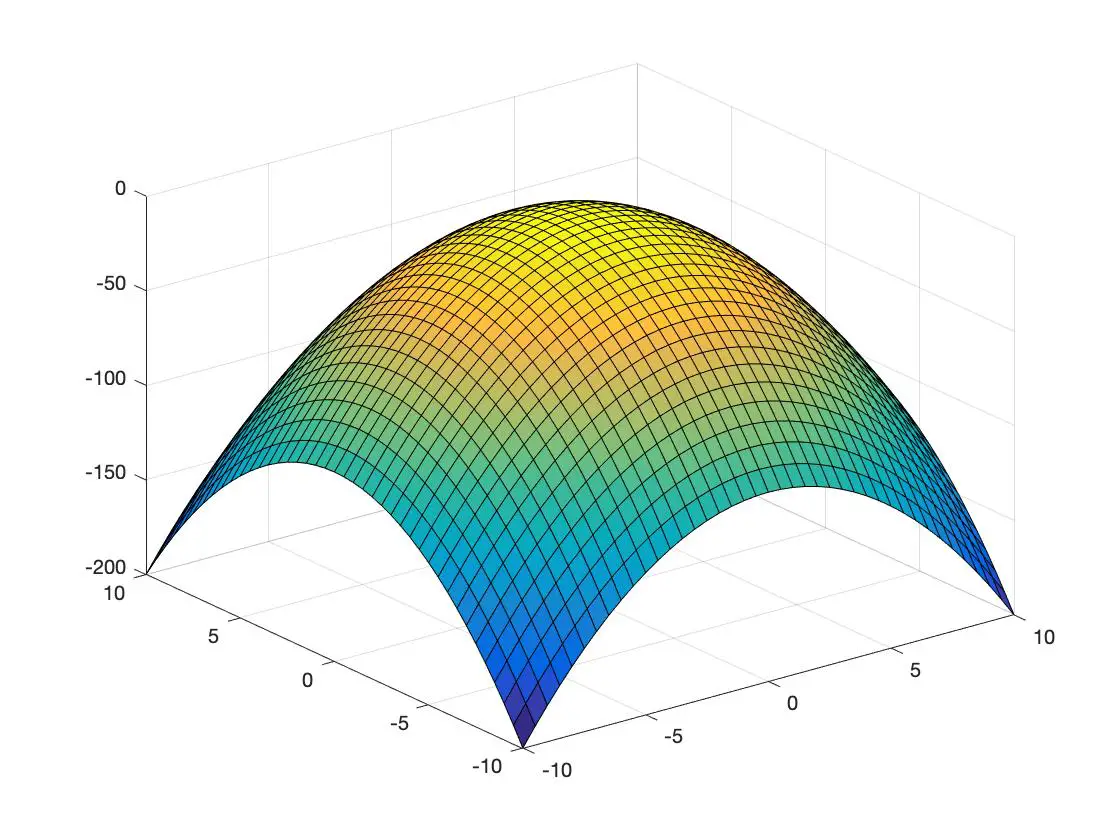
Abaixo você tem um exemplo de função convexa e outro de função côncava representada em um espaço tridimensional:

função convexa

função côncava

A imagem possui um atributo ALT vazio; seu nome de arquivo é concavidade-e-convexidade-de-uma-função-com-a-matriz-hessiana-1024x768.jpg

Mais aplicações da matriz Hessiana

Os principais usos da matriz Hessiana são os que já vimos, porém, ela também possui outras aplicações. Explicamos-los abaixo para os mais curiosos.

Polinômio de Taylor

A expansão do polinômio de Taylor para funções de 2 ou mais variáveis no ponto

$a$

começa assim:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

Como você pode ver, os termos de segunda ordem da expansão de Taylor são dados pela matriz Hessiana avaliada no ponto de expansão do polinômio.

Matriz de serapilheira com bordas

Outro uso da matriz Hessiana é calcular os mínimos e máximos de uma função multivariada

$f(x,y)$

restrito a outra função

$g(x,y)$

. Para resolver este problema, utiliza-se a matriz Hessiana limitada e segue-se o seguinte procedimento:

Passo 1: Calcula-se a função de Lagrange, que é definida pela seguinte expressão:

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

Passo 2: Os pontos críticos da função de Lagrange são encontrados. Para fazer isso, calculamos o gradiente da função de Lagrange, igualamos as equações a 0 e resolvemos as equações.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

Etapa 3: Para cada ponto encontrado, calculamos o Hessiano limitado, que é definido pela seguinte matriz:

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

Etapa 4: Determinamos para cada ponto crítico se é máximo ou mínimo:

Este será um máximo local da função
$f$

sob restrições de função

$g$

se o último nm (onde n é o número de variáveis em o número de restrições) os principais menores da matriz Hessiana com borda avaliada no ponto crítico têm sinais alternados começando com o sinal negativo.

Este será um mínimo local da função
$f$

sob restrições de função

$g$

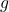
se o último nm (onde n é o número de variáveis em o número de restrições), os principais menores da matriz Hessiana acentuada avaliada no ponto crítico têm todos sinais negativos.

Deve-se ter em mente que os mínimos ou máximos relativos de uma função restrita para outra não precisam necessariamente ser assim para a função irrestrita. A matriz Hessiana com borda é, portanto, útil apenas para este tipo de problema.

Relacionamento com outras operações

Por fim, a matriz Hessiana também está ligada a outras operações ou matrizes importantes, principalmente com a matriz Jacobiana e com o operador de Laplace.

Relação com a matriz Jacobiana

A matriz Hessiana de uma função

$f$

é a matriz Jacobiana do gradiente da mesma função:

$\displaystyle H_f = J(\nabla f)$

Operador Laplace

O traço da matriz Hessiana é equivalente ao operador Laplace :

$\displaystyle tr( H_f) = \Delta f$

Esta igualdade pode ser facilmente comprovada, pois a definição do operador de Laplace é a divergência do gradiente de uma função:

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

Sua expressão é portanto:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

E esta soma é apenas o traço da matriz Hessiana, então a equivalência está provada.

Matriz hessiana (ou hesse)

Qual é a matriz Hessiana?

Exemplo de cálculo da matriz Hessiana

Problemas resolvidos de matrizes Hessianas

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Como saber quando a matriz Hessiana é positiva, negativa ou indefinida?

Critério de autovalores (ou autovalores)

Critério de Sylvester

Como calcular o máximo ou mínimo de uma função com a matriz Hessiana

Exemplo de cálculo de máximos e mínimos de uma função multivariável

Determinando a concavidade ou convexidade de uma função com a matriz Hessiana

Mais aplicações da matriz Hessiana

Polinômio de Taylor

Matriz de serapilheira com bordas

Relacionamento com outras operações

Relação com a matriz Jacobiana

Operador Laplace

Deixe um comentário Cancelar resposta