Matriz diagonal - Matoridade

Nesta página você verá o que é uma matriz diagonal e exemplos de matrizes diagonais. Além disso, você descobrirá como operar com este tipo de matrizes, como calcular facilmente seus determinantes e como invertê-los. Existem também propriedades e aplicações de matrizes diagonais. E, finalmente, há as explicações de uma matriz bidiagonal e de uma matriz tridiagonal.

O que é uma matriz diagonal?

Uma matriz diagonal é uma matriz quadrada em que todos os elementos que não estão na diagonal principal são zero (0). Os elementos da diagonal principal podem ou não ser zero.

Assim que soubermos a definição exata de uma matriz diagonal, veremos exemplos de matrizes diagonais:

Exemplos de matrizes diagonais

Exemplo de uma matriz diagonal de dimensão 2 × 2

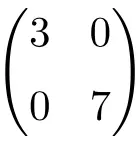
Exemplo de matriz diagonal de ordem 3×3

Exemplo de matriz diagonal de tamanho 4×4

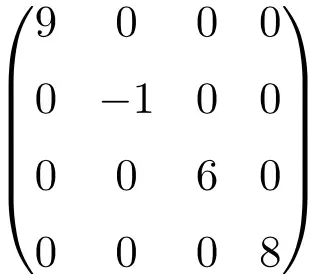
Esses tipos de matrizes são geralmente escritos indicando os elementos da diagonal:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Operações com matrizes diagonais

Uma das razões pelas quais as matrizes diagonais são tão importantes para a álgebra linear é a facilidade com que permitem realizar cálculos. É por isso que eles são tão usados em matemática.

Adicionando e subtraindo matrizes diagonais

Adicionar (e subtrair) duas matrizes diagonais é muito simples: basta adicionar (ou subtrair) os números nas diagonais.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Por exemplo:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Multiplicação de matriz diagonal

Para resolver uma multiplicação ou produto matricial de duas matrizes diagonais, basta multiplicar os elementos das diagonais.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Por exemplo:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Poder de matrizes diagonais

Para calcular a potência de uma matriz diagonal, precisamos elevar cada elemento da diagonal ao expoente:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Por exemplo:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Determinante de uma matriz diagonal

O determinante de uma matriz diagonal é o produto dos elementos da diagonal principal.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Veja o seguinte exercício resolvido no qual encontramos o determinante de uma matriz diagonal simplesmente multiplicando os elementos de sua diagonal principal:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Este teorema é fácil de provar: basta calcular o determinante de uma matriz diagonal por blocos (ou cofatores). Esta demonstração é detalhada abaixo usando uma matriz diagonal genérica:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Inverter uma matriz diagonal

Uma matriz diagonal é invertível se e somente se todos os elementos da diagonal principal forem diferentes de 0 . Neste caso dizemos que a matriz diagonal é uma matriz regular.

Além disso, a inversa de uma matriz diagonal será sempre outra matriz diagonal com as inversas da diagonal principal:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Da característica anterior, podemos deduzir que o determinante da inversa de uma matriz diagonal é o produto das inversas da diagonal principal:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Propriedades de matrizes diagonais

Qualquer matriz diagonal também é uma matriz simétrica .

Uma matriz diagonal é uma matriz triangular superior e inferior .

A matriz identidade é uma matriz diagonal:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Da mesma forma, a matriz zero também é uma matriz diagonal, pois todos os seus elementos que não estão na diagonal são zeros. Embora os números na diagonal sejam 0.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Os autovalores (ou autovalores) de uma matriz diagonal são os elementos de sua diagonal principal.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Uma matriz quadrada é diagonal se e somente se for triangular e normal .

O adjunto de uma matriz diagonal é outra matriz diagonal.

Aplicações de matriz diagonal

Como vimos, resolver cálculos com matrizes diagonais é muito simples, pois muitos zeros estão envolvidos nas operações. Por esse motivo, são muito úteis no campo da matemática e são amplamente utilizados.

Por esse mesmo motivo, tantos estudos foram feitos sobre como diagonalizar uma matriz e, de fato, até foi desenvolvido um método para diagonalizar matrizes (usando o polinômio característico).

Portanto, matrizes diagonalizáveis também são bastante relevantes. Como o teorema da decomposição espectral, que estabelece as condições para quando uma matriz pode ser diagonalizada e quando não o é.

matriz bidiagonal

Uma matriz bidiagonal é uma matriz quadrada em que todos os elementos que não estão na diagonal principal ou na diagonal superior ou inferior são 0.

Por exemplo:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

matriz bidiagonal superior

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

matriz bidiagonal inferior

Quando a diagonal principal e a primeira superdiagonal estão ocupadas, falamos de uma matriz bidiagonal superior. Por outro lado, quando a diagonal principal e a primeira subdiagonal estão ocupadas, falamos de uma matriz bidiagonal inferior.

matriz tridiagonal

Uma matriz tridiagonal é uma matriz quadrada cujos únicos elementos diferentes de zero são os da diagonal principal e as diagonais adjacentes acima e abaixo.

Por exemplo:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Assim, todas as matrizes diagonais, bidiagonais e tridiagonais são exemplos de matrizes de banda . Porque uma matriz de banda é aquela matriz que possui todos os seus elementos diferentes de zero em torno da diagonal principal.

O que é uma matriz diagonal?

Exemplos de matrizes diagonais

Operações com matrizes diagonais

Adicionando e subtraindo matrizes diagonais

Multiplicação de matriz diagonal

Poder de matrizes diagonais

Determinante de uma matriz diagonal

Inverter uma matriz diagonal

Propriedades de matrizes diagonais

Aplicações de matriz diagonal

matriz bidiagonal

matriz tridiagonal

Deixe um comentário Cancelar resposta