Matriz anti-hermitiana (ou anti-hermitiana)

Nesta página você verá o que é uma matriz anti-hermitiana, também chamada de matriz anti-hermitiana. Você encontrará exemplos de matrizes anti-Hermitianas, todas as suas propriedades e a forma deste tipo de matrizes quadradas complexas. Finalmente, você encontrará a explicação de como decompor qualquer matriz complexa na soma de uma matriz anti-Hermitiana mais outra matriz Hermitiana.

O que é uma matriz anti-hermitiana ou anti-hermitiana?

Uma matriz anti-Hermitiana , ou também chamada de matriz anti-Hermitiana, é uma matriz quadrada com números complexos cuja transposta conjugada é igual à mesma matriz, mas de sinais diferentes.

A^*=-A

Ouro

A^*

é a matriz conjugada transposta de

A

.

A título de curiosidade, este tipo de matriz é assim chamada porque preenche a condição oposta da matriz Hermitiana , cujo nome vem do importante matemático francês Charles Hermite, professor e pesquisador de matemática do século XIX que fez importantes estudos inclusive em o campo da álgebra linear.

Exemplos de matrizes anti-hermitianas

Depois de vermos a definição de matriz anti-hermitiana (ou matriz anti-hermitiana) veremos alguns exemplos de matrizes anti-hermitianas de diferentes dimensões:

Exemplo de uma matriz anti-Hermitiana de ordem 2×2

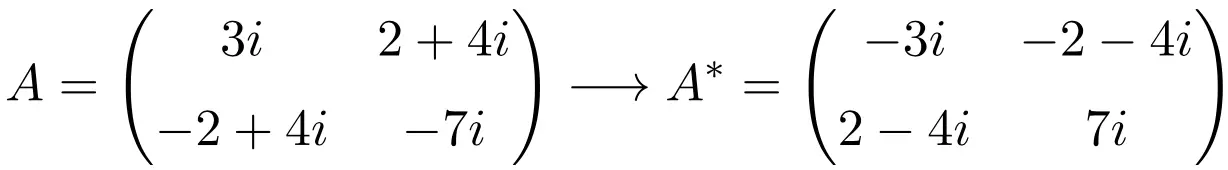
matriz anti-hermitiana ou anti-hermitiana de dimensão 2x2

Exemplo de uma matriz anti-hermitiana de dimensão 3×3

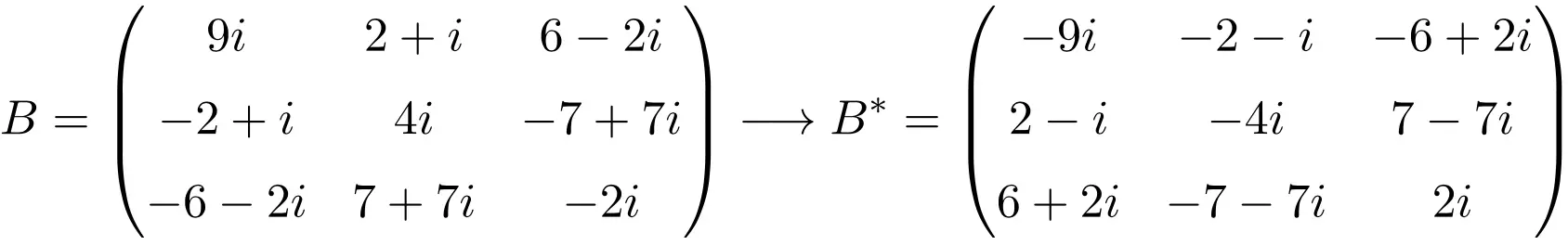
matriz anti-hermitiana ou anti-hermitiana de dimensão 3x3

Exemplo de uma matriz anti-hermitiana de tamanho 4×4

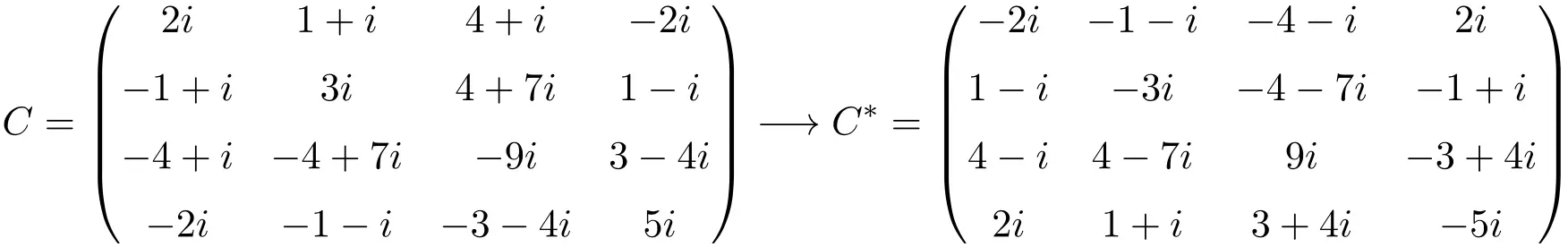
matriz anti-hermitiana ou anti-hermitiana de dimensão 4x4

Como você pode ver, as matrizes A, B e C são anti-Hermitianas porque a matriz transposta conjugada de cada uma é igual à própria matriz, mas com todos os elementos alterados de sinal.

Estrutura de uma matriz anti-hermitiana

Se você já viu os exemplos anteriores, as matrizes anti-Hermitianas sempre têm a mesma estrutura: são compostas por números imaginários (sem parte real) na diagonal principal, e o elemento complexo localizado na i-ésima linha e na j-ésima linha linha. coluna deve ter a mesma parte imaginária e a mesma parte real, mas com sinal alterado como o elemento da j-ésima linha e da i-ésima coluna.

Embora isto possa parecer um pouco complicado, certamente é melhor compreendido pelo exemplo a seguir:

Estrutura de uma matriz anti-hermitiana de dimensão 2×2

\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}

Como você pode ver, os elementos da diagonal principal de uma matriz anti-Hermitiana são totalmente imaginários e os elementos da diagonal secundária possuem a mesma parte imaginária e a parte real mudou de sinal.

Portanto, a parte real de uma matriz anti-Hermitiana deve ser antissimétrica e a parte imaginária simétrica.

Propriedades da matriz anti-hermitiana

Veremos agora quais são as propriedades deste tipo de matriz quadrada complexa:

  • Cada matriz anti-hermitiana é um exemplo de matriz normal . Embora nem todas as matrizes normais sejam matrizes anti-hermíticas.
  • Qualquer matriz anti-Hermitiana é diagonalizável. Além disso, a matriz diagonal resultante contém apenas elementos puramente imaginários.
  • Portanto, os autovalores (ou autovalores) de uma matriz anti-Hermitiana são sempre números imaginários.
  • Da mesma forma, os autovetores (ou autovetores) de diferentes autovalores de uma matriz anti-Hermitiana são ortogonais.
  • Uma matriz de números reais, ou seja, que nenhum elemento tem parte imaginária, é anti-Hermitiana se e somente se for uma matriz antissimétrica .
  • Uma matriz anti-Hermitiana pode ser expressa como a soma de uma matriz antissimétrica real e uma matriz simétrica imaginária.

A =B+Ci

  • A soma (ou subtração) de duas matrizes anti-Hermitianas é igual a outra matriz anti-Hermitiana.
  • O resultado do produto de uma matriz anti-Hermitiana e um escalar é outra matriz anti-Hermitiana se o escalar for um número real.
  • A potência de uma matriz anti-Hermitiana é igual a uma matriz anti-Hermitiana se o expoente for ímpar; por outro lado, se for elevado a um expoente par, o resultado será uma matriz Hermitiana.
  • Sim

    A

    é uma matriz anti-hermitiana, então o produto

    iA

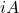
    é uma matriz Hermitiana.

Decomposição de uma matriz complexa em uma matriz anti-Hermitiana e uma matriz Hermitiana

Qualquer matriz contendo números complexos pode ser decomposta na soma de uma matriz anti-Hermitiana mais outra matriz Hermitiana . Mas para isso você precisa conhecer as seguintes características desses tipos de matrizes:

  • A soma de uma matriz quadrada complexa mais seu conjugado transposto é equivalente a uma matriz Hermitiana (ou Hermitiana):

C + C^* = \text{Matriz Hermitiana}

  • A diferença entre uma matriz quadrada complexa e seu conjugado transposto é igual a uma matriz anti-Hermitiana:

C - C^* = \text{Matriz Antihermitiana}

  • Portanto, todas as matrizes complexas podem ser decompostas na soma de uma matriz Hermitiana e uma matriz anti-Hermitiana. Este teorema é conhecido como decomposição de Teoplitz :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Onde C é a matriz complexa que queremos decompor, C* seu conjugado transposto e finalmente A e B são respectivamente as matrizes Hermitiana e anti-Hermitiana nas quais a matriz C é decomposta.

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima