Limites laterais - Matoridade

Neste artigo explicamos o que é o limite lateral de uma função (com exemplos). Também ensinamos como calcular os limites laterais esquerdo e direito de uma função, tanto gráfica quanto numericamente. Além disso, você poderá treinar com exercícios resolvidos passo a passo dos limites laterais.

Quais são os limites laterais?

Os limites laterais de uma função num ponto estudam o comportamento da função em torno desse ponto. Existe o limite lateral esquerdo e o limite lateral direito, que analisa o valor da função à esquerda e à direita do ponto considerado respectivamente.

Limites laterais esquerdo e direito

Como vimos na definição dos limites laterais, existem dois tipos: limites laterais esquerdos e limites laterais direitos.

O limite esquerdo da função é expresso por um sinal de menos no ponto onde o limite é analisado e, por outro lado, o limite direito é indicado pelo sinal de mais.

Limite lateral à esquerda

$\displaystyle\lim_{x\to a^{\color{orange}\bm{-}\color{black}}}f(x)$

Limite lateral à direita

$\displaystyle\lim_{x\to a^{\color{orange}\bm{+}\color{black}}}f(x)$

Veja o exemplo a seguir para entender melhor o significado dos limites laterais:

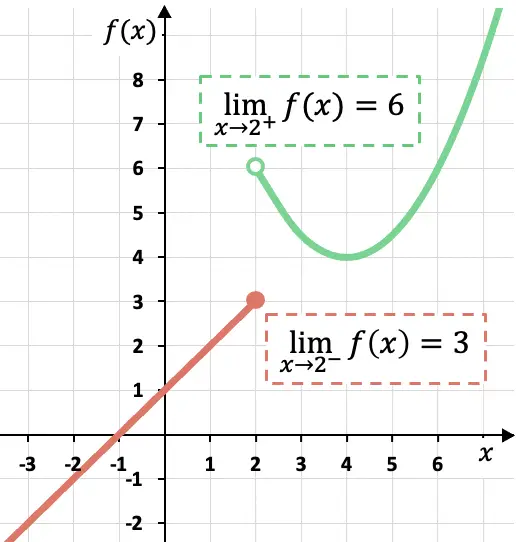
Como você pode ver na representação gráfica desta função por partes, os limites laterais dependem do lado em que são calculados.

Nesse caso, a função se aproxima de 3 quando x se aproxima de 2 pela esquerda, já que a função assume valores mais próximos de 3 quando x se aproxima de x=2 pela sua esquerda.

Por outro lado, o limite lateral da função em x=2 pela reta vale 6. Porque se nos aproximarmos do ponto x=2 pela sua reta, a função assume valores cada vez mais próximos de f(x)= 6.

Por outro lado, você deve saber que os limites laterais têm as mesmas propriedades dos limites normais. No link a seguir você pode ver quais são as propriedades dos limites:

➤ Veja: propriedades de limite

limites laterais iguais

Acabamos de ver um exemplo onde os limites laterais de uma função são diferentes, mas… o que acontece se os limites laterais forem iguais?

Se ambos os limites laterais de uma função num ponto existem e são iguais , o limite da função existe nesse ponto e o resultado do limite é o valor dos limites laterais.

Em outras palavras, para que o limite de uma função exista em um ponto, a seguinte condição deve ser atendida:

$\displaystyle\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L \ \iff \ \lim_{x\to a}f(x)=L$

Portanto, se os limites laterais de uma função num ponto forem diferentes, o limite da função nesse ponto não existe.

Além disso, que exista o limite de uma função em um ponto é uma condição essencial para que ela seja uma função contínua em um ponto .

Vamos resolver um exemplo para finalizar o entendimento do conceito de limites laterais:

Os limites laterais no ponto x=-2 da função representada graficamente coincidem, pois o valor da função tende para 3 quer nos aproximemos de x=-2 pela esquerda ou pela direita. Portanto, o limite da função em x=-2 é igual a 3.

$\displaystyle\lim_{x\to -2^-}f(x)=\lim_{x\to -2^+}f(x)=3 \ \longrightarrow \ \lim_{x\to -2}f(x)=3$

Por outro lado, no ponto x=4 os limites laterais são diferentes, pois pela esquerda a função se aproxima de f(x)=3 mas pela direita a função se aproxima de f(x)=2. O limite da função neste ponto, portanto, não existe.

$\displaystyle\lim_{x\to 4^-}f(x)=3 \neq \lim_{x\to 4^+}f(x)=2 \ \longrightarrow \ \cancel{\exists} \ \lim_{x\to 4}f(x)$

Cálculo dos limites laterais

Dada a definição dos limites laterais, veremos como eles são calculados numericamente resolvendo o seguinte exemplo:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}$

Se calcularmos o limite normalmente, obteremos a indeterminação de um número real dividido por 0:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}=\frac{3}{2-2}=\frac{3}{0}=\infty$

Porém, ao calcular os limites laterais, não obtemos nenhuma indeterminação.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\ \color{red}\bm{?}\color{black} \qquad \lim_{x\to 2^+}\frac{3}{x-2}=\ \color{red}\bm{?}$

Para calcular o limite lateral da função à esquerda em x=2, você deve pegar um número menor que x=2, mas muito próximo dele, por exemplo x=1,999.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{\color{red}\bm{1,999}\color{black}-2}$

Neste caso o denominador será um número negativo com um valor muito pequeno mas nem sequer zero, e é geralmente representado por um zero e um sinal de menos na frente dele:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{\color{red}\bm{-0}\color{black}}$

Portanto, o resultado do limite lateral é menos infinito, pois qualquer número dividido por 0 dá infinito, e positivo dividido por negativo dá negativo:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{-0}=\color{red}\bm{-\infty}\color{black}$

Podemos verificar que a função se aproxima de menos infinito computando imagens da função com valores mais próximos de x=2 a partir da esquerda.

$\begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}$

Da mesma forma, para encontrar o limite da função no ponto x=2 à direita, podemos aplicar o mesmo raciocínio: tomamos um valor maior que 2 mas muito próximo, como 2001.

$\displaystyle\lim_{x\to 2^+}\frac{3}{x-2}=\frac{3}{2,001-2}=\frac{3}{+0}=+\infty$

Da mesma forma, podemos verificar que a função tende ao infinito calculando imagens da função com valores cada vez mais próximos de x=2 à direita.

$\begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}$

No gráfico a seguir você pode ver representada a função analisada. Como você pode ver, o limite lateral da função no ponto x=2 à esquerda é menos infinito, e o limite lateral da função no ponto x=2 à direita é mais infinito.

Problemas de limite lateral corrigidos

Exercício 1

Encontre os limites laterais da seguinte função definida por partes nos pontos onde a definição muda (x=-2 ex=4).

veja solução

Os limites laterais não coincidem no ponto x=-2, à esquerda a função tende para f(x)=5 e, por outro lado, à direita a função é constante e vale 3.

$\displaystyle\lim_{x\to -2^-}f(x)=5$

$\displaystyle\lim_{x\to -2^+}f(x)=3$

Os limites laterais também são diferentes à medida que x se aproxima de 4. A função por partes se aproxima de 3 pela esquerda, mas se aproxima de -2 pela direita.

$\displaystyle\lim_{x\to 4^-}f(x)=3$

$\displaystyle\lim_{x\to 4^+}f(x)=-2$

Exercício 2

Determine se o limite existe quando x se aproxima de 3 da seguinte função por partes e, em caso afirmativo, qual é o seu valor.

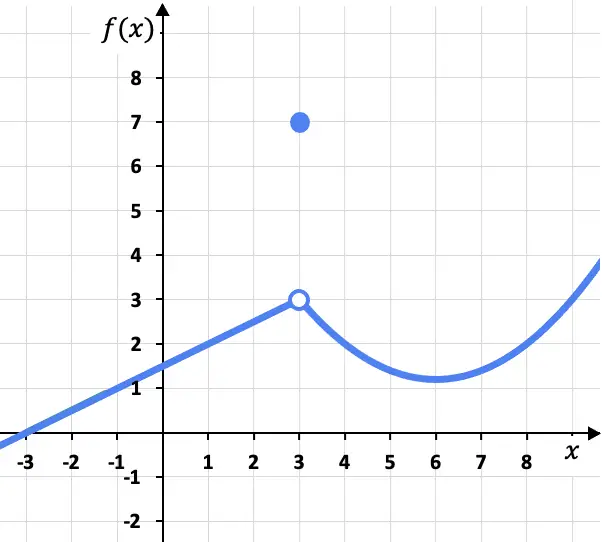
Limites laterais de uma função por partes

veja solução

Neste problema, os limites laterais no ponto x=3 à esquerda e à direita são idênticos, pois a função tende para o mesmo valor (f(x)=3) quer seja abordada pela esquerda ou pela direita . seu lado direito:

$\displaystyle\lim_{x\to 3^-}f(x)=3$

$\displaystyle\lim_{x\to 3^+}f(x)=3$

Portanto, de acordo com a definição matemática do limite, o limite da função quando x tende a 3 é igual a 3, porque os dois limites laterais neste mesmo ponto coincidem neste valor:

$\displaystyle\lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=3 \ \longrightarrow \ \lim_{x\to 3}f(x)=3$

Embora o limite da função em x=3 seja 3, deve-se levar em conta que a função neste ponto não é 3, mas sim que f(3)=7. Como veremos mais tarde, isto significa que a função não é contínua em x=3, mas sim tem uma descontinuidade evitável.

Exercício 3

Calcule os limites laterais da seguinte função racional no ponto x=4.

$f(x)=\cfrac{-2x+3}{x-4}$

veja solução

Para calcular o limite quando x tende para 4 pela esquerda, tomamos um valor menor que 4, mas muito próximo dele, por exemplo 3.999:

$\displaystyle\lim_{x\to 4^-}\frac{-2x+3}{x-4}=\frac{-2\cdot 3,999+3}{3,999-4}=\frac{-4,998}{-0}=+\infty$

Portanto, o limite lateral quando x se aproxima de 4 pela esquerda é mais infinito.

E para resolver o limite quando x tende para 4 pela direita, avaliamos a função em um valor maior que 4 mas muito próximo dele, por exemplo 4.001:

$\displaystyle\lim_{x\to 4^+}\frac{-2x+3}{x-4}=\frac{-2\cdot 4,001+3}{4,001-4}=\frac{-5,002}{+0}=-\infty$

Portanto, o limite lateral quando x se aproxima de 4 pela direita é menos infinito.

Exercício 4

Encontre o limite, se existir, da seguinte função por partes definida no ponto x=2:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p> </p> <div class=$

veja solução

Neste caso, a definição do problema pede-nos para determinar o limite onde a função por partes muda de expressão, por isso precisamos de determinar o limite no lado esquerdo utilizando a primeira expressão e o limite no lado direito utilizando a segunda expressão.

$\displaystyle\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}\frac{-3x+5}{x-3}=\frac{-3\cdot 2+5}{2-3}=\frac{-1}{-1}=1$

O limite da função em x=2 à esquerda coincide com o limite da função à direita, então o limite da função existe e é igual a 1:

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^+}f(x)=1 \ \longrightarrow \ \lim_{x\to 2}f(x)=1$

Quais são os limites laterais?

Limites laterais esquerdo e direito

limites laterais iguais

Cálculo dos limites laterais

Problemas de limite lateral corrigidos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta