▷ Como resolver limites no infinito (+25 exercícios resolvidos)

Aqui você encontrará como resolver todos os tipos de limites no infinito: funções polinomiais, racionais, exponenciais, com raízes, indeterminações no infinito… Além disso, você poderá treinar com 25 exercícios resolvidos passo a passo sobre limites quando x tendem ao infinito. .

Limite de uma função quando x tende ao infinito

O limite de uma função quando x se aproxima do infinito , seja positivo ou negativo, pode ser um valor real, mais infinito, menos infinito ou inexistente. Para resolver os limites no infinito, você precisa substituir x pelo infinito.

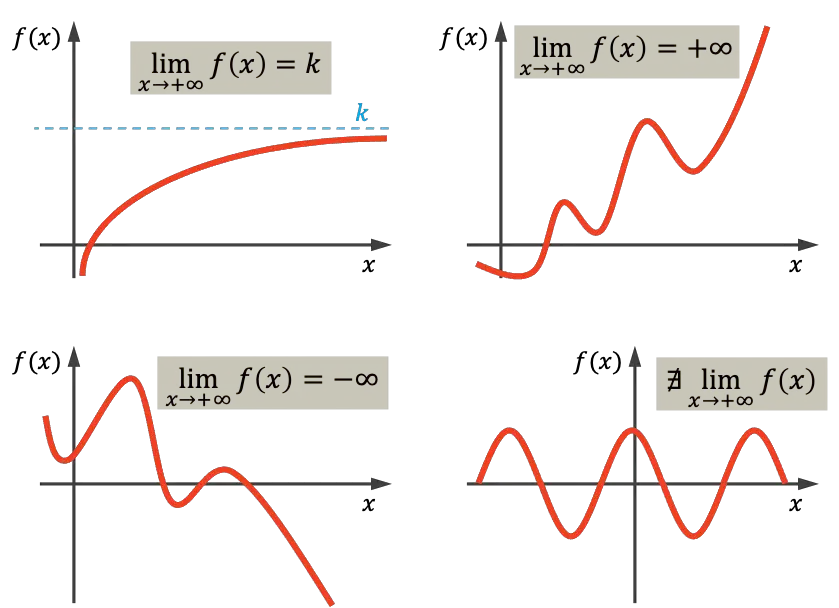
Como você pode ver no primeiro gráfico, a função mostrada tende ao valor real k em direção ao infinito, porque se aproxima de k à medida que x cresce. A função no canto superior direito tende ao infinito à medida que x se aproxima do infinito, porque cresce indefinidamente à medida que x aumenta de valor. Por outro lado, o gráfico no canto inferior esquerdo diminui sem parar e, portanto, tende para menos infinito. Por fim, a última função é periódica e não tende a nenhum valor, portanto não há limite para o infinito neste caso.

Como resolver limites no infinito

Para resolver um limite ao infinito em funções polinomiais, devemos substituir x por infinito apenas no termo de maior grau da função.

Por exemplo, observe o seguinte cálculo de um limite ao infinito, onde substituímos apenas o infinito no monômio do grau mais alto:

$\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}$

Como você pode ver no exemplo, +∞ ao quadrado dá +∞, já que um número muito grande (+∞) elevado à potência de 2 sempre dará um número muito grande (+∞).

E o mesmo acontece com a multiplicação: se você multiplicar um número muito grande (+∞), sempre obterá um número muito grande (+∞). Por exemplo:

$3\cdot (+\infty)= +\infty.$

Atenção: para calcular limites ao infinito é importante levar em consideração os seguintes elementos:

→ Um número negativo elevado a um expoente par é positivo. Portanto, menos infinito elevado a um expoente par dá mais infinito:

$(-\infty)^2 = +\infty$

→ Um número negativo elevado a um expoente ímpar é negativo. Portanto, menos infinito elevado a um expoente ímpar é menos infinito:

$(-\infty)^3 = -\infty$

→ Multiplicar um número negativo altera o sinal do infinito:

$-2(+\infty) = - \infty$

→ Qualquer número dividido por

$\pm \infty$

dá 0:

$\cfrac{5}{\infty} = 0$

Exemplos de limites ao infinito

Para que você possa ver como os limites ao infinito são resolvidos em polinômios, abaixo estão vários desses limites resolvidos:

$\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}$

Limites indeterminados ao infinito

Os limites ao infinito nem sempre serão tão fáceis de calcular, pois às vezes obteremos a indeterminação do infinito entre o infinito ou a indeterminação do infinito menos o infinito.

$\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty$

Quando obtemos este tipo de indeterminações (ou formas indeterminadas), não podemos conhecer o resultado diretamente, mas devemos realizar um procedimento preliminar para encontrar o valor limite. Veremos então como os limites indeterminados no infinito são resolvidos.

Indeterminação infinita entre o infinito

Para encontrar o resultado da indeterminação infinito dividido pelo infinito devemos comparar o grau do numerador e o grau do denominador da fração:

Se o grau do polinômio do numerador for menor que o grau do polinômio do denominador, a indeterminação infinita sobre o infinito é igual a zero.
Se o grau do polinômio do numerador for equivalente ao grau do polinômio do denominador, a indeterminação infinita sobre o infinito é o quociente dos coeficientes principais dos dois polinômios.
Se o grau do polinômio do numerador for maior que o grau do polinômio do denominador, a indeterminação infinita entre o infinito dá mais ou menos infinito (o sinal depende dos termos principais dos dois polinômios).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> Por exemplo, no limite a seguir, o polinômio do numerador é de segundo grau, enquanto o polinômio do denominador é de terceiro grau, então a solução para o limite é 0. <p class=$ $\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Veja este outro exemplo, em que os dois polinômios da função racional são de segundo grau, portanto devemos dividir os coeficientes dos termos de grau superior para calcular o limite no infinito.

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Finalmente, no próximo limite, a função do numerador tem um grau maior que a do denominador, então a indeterminação do infinito no infinito dá o infinito. Além disso, um infinito positivo é obtido do numerador, mas um infinito negativo do denominador, então o resultado do limite é negativo (o positivo entre o negativo é negativo).

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Indeterminação infinita entre o infinito com raízes

Por outro lado, o grau de uma função irracional (função com raízes) é o quociente entre o grau do termo principal e o índice do radical.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Portanto, se o limite de uma função com raízes dá indeterminação infinita entre o infinito , devemos aplicar as mesmas regras explicadas acima em relação aos graus do numerador e do denominador, mas levando em consideração que o grau de um polinômio com raízes é calculado de forma diferente.

Veja o seguinte exemplo do limite infinito de uma função com radicais:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

O grau do numerador é 2 e o grau do denominador é 4 (8/2=4), então o limite é 0 porque o grau do numerador é menor que o grau do denominador.

Indeterminação infinita entre o infinito com funções exponenciais

O crescimento de uma função exponencial é muito maior que o crescimento de uma função polinomial, portanto devemos considerar que o grau de uma função exponencial é maior que o grau de uma função polinomial.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Assim, se a indeterminação infinito dividido por infinito resulta de um limite com funções exponenciais, devemos simplesmente aplicar as mesmas regras explicando os graus do numerador e do denominador, mas tendo em conta que uma função exponencial é de ordem superior a um polinómio. Além disso, se tivermos funções exponenciais no numerador e no denominador da divisão, a função exponencial com maior base será a de maior ordem. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

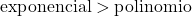
Neste exemplo, o denominador é formado a partir de uma função exponencial, portanto é de ordem superior ao numerador. Portanto, a forma indeterminada infinito entre o infinito dá 0.

Infinito menos indeterminação infinita

Resolver a indeterminação infinita menos infinita depende se a função tem frações ou raízes. Então vamos ver como resolver esse tipo de indeterminação para esses dois casos diferentes.

Indeterminação infinita menos infinita com frações

Quando ocorre uma indeterminação infinita menos infinita em uma adição ou subtração de frações algébricas , devemos primeiro fazer a adição ou subtração das frações e depois calcular o limite.

Vamos ver como calcular a indeterminação infinito menos infinito em uma função com frações resolvendo um exemplo passo a passo:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

Primeiro tentamos calcular o limite:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Mas obtemos a indeterminação ∞-∞.

Devemos primeiro subtrair as frações. Para isso, reduzimos as frações a um denominador comum, ou seja, multiplicamos o numerador e o denominador de uma fração pelo denominador da outra:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

E agora que as duas frações têm o mesmo denominador, podemos combiná-las numa única fração:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

Operamos no numerador e no denominador:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

E finalmente calculamos o limite novamente:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Neste caso a indeterminação infinita entre o infinito dá +∞ porque o grau do numerador é maior que o grau do denominador.

Indeterminação infinita menos infinita com raízes

Quando ocorre indeterminação infinita menos infinita na adição ou subtração radical , devemos primeiro multiplicar e dividir a função pela expressão radical conjugada e depois resolver o limite.

Vamos ver como resolver a indeterminação infinito menos infinito em uma função irracional seguindo um exemplo passo a passo:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

Primeiro tentamos resolver o limite da função com radicais:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

No entanto, obtemos a forma indeterminada ∞-∞. Então para saber quanto de indeterminação é infinito menos infinito você tem que aplicar o procedimento explicado.

Como a função possui radicais, multiplicamos e dividimos toda a função pela expressão irracional conjugada:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

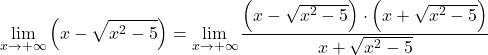
A expressão algébrica do numerador corresponde à identidade notável do produto de uma soma e uma diferença, podemos portanto simplificar a expressão:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

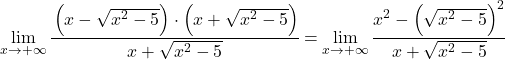
Agora simplificamos a raiz do limite, já que é elevado ao quadrado:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

Operamos no numerador da fração:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

E por fim, refazemos o cálculo do limite:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

O resultado do limite é portanto 0, porque qualquer número dividido pelo infinito é igual a zero.

Exercícios resolvidos sobre limites no infinito

Exercício 1

Encontre os seguintes limites da função gráfica:

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

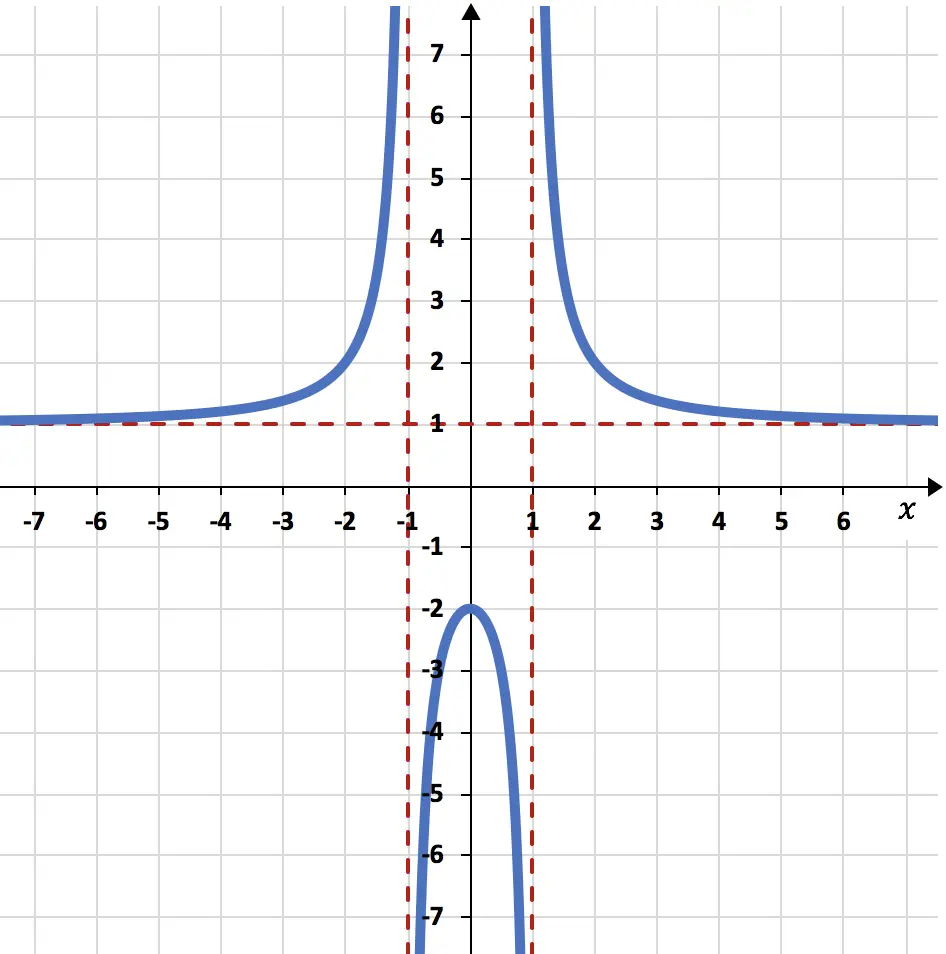
limites ao infinito a partir da representação de uma função

Veja a solução

O limite da função quando x tende para menos infinito e mais infinito dá 1:

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

Os limites laterais da função à esquerda e à direita no ponto x=-1 são respectivamente mais infinito e menos infinito:

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

Finalmente, os limites laterais da função quando x tende a 1 valem menos infinito e mais infinito:

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

Exercício 2

Resolva o limite quando x se aproxima de mais o infinito da seguinte função:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

Veja a solução

Para resolver o limite no infinito, precisamos substituir x pelo infinito no termo de maior grau do polinômio:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

Exercício 3

Calcule o limite ao infinito da seguinte função polinomial:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

Veja a solução

Para resolver o limite no infinito, substituímos x por infinito no termo de grau mais alto do polinômio e realizamos os cálculos:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

Exercício 4

Resolva o limite pelo menos infinito da seguinte função polinomial:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

Veja a solução

Para calcular o limite no infinito, substituímos x por menos infinito no grau mais alto do termo do polinômio e avaliamos a função:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

Como menos infinito é elevado ao quadrado, o sinal do infinito torna-se positivo.

Exercício 5

Encontre o limite no infinito da seguinte função racional:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

Veja a solução

Para determinar o limite ao infinito, substituímos x por mais infinito no termo do maior grau do numerador e denominador da fração:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

Lembre-se de que qualquer número dividido por mais ou menos infinito é igual a 0.

Exercício 6

Resolva o seguinte limite no infinito:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

Veja a solução

Para calcular o limite quando x tende para ±∞ de uma função, basta olhar para o monômio do grau mais alto da função:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

Exercício 7

Calcule o limite da seguinte função quando x se aproxima do infinito negativo:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

Veja a solução

Neste caso, basta substituir o termo quadrático por infinito:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

Exercício 8

Encontre o limite da seguinte função exponencial quando x se aproxima do infinito:

$\displaystyle \lim_{x \to +\infty} 2^x$

Veja a solução

Embora seja uma função exponencial, o processo para resolver o limite é o mesmo: substitua x pelo infinito.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

Exercício 9

Resolva o limite infinito da seguinte função exponencial:

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

Veja a solução

Para resolver esse limite você deve usar as propriedades das frações:

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

Exercício 10

Resolva o seguinte limite no infinito:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Veja a solução

O limite dá indeterminação menos infinito entre mais infinito. O grau do numerador é maior que o grau do denominador, então o limite indeterminado é igual a mais infinito. Porém, como a divisão é infinito negativo por infinito positivo, o resultado é infinito negativo.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Exercício 11

Corrija o seguinte limite indeterminado:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Veja a solução

Neste problema, a forma indeterminada infinito sobre infinito é obtida a partir do quociente de dois polinômios de mesmo grau, portanto o resultado do limite indeterminado é a divisão de seus coeficientes principais:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Exercício 12

Calcule o seguinte limite pelo menos até o infinito:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Veja a solução

O grau de expressão algébrica do numerador é menor que o grau de expressão do denominador, então a indeterminação +∞/+∞ dá 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Exercício 13

Resolva o seguinte limite indeterminado de uma função com raízes:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Veja a solução

A expressão do numerador está sob radical, seu grau é portanto 7/3. Por outro lado, o polinômio denominador é quadrático. E como 7/3>2, o limite dá mais infinito:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Exercício 14

Determine o limite infinito da seguinte função com frações:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Veja a solução

Neste exercício obtemos indeterminação menos infinito dividido por menos infinito com o grau do numerador maior que o grau do denominador, portanto:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Exercício 15

Encontre o limite pelo menos infinito da seguinte função:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Veja a solução

O polinômio denominador é quadrático, enquanto o polinômio numerador é linear. Portanto, a indeterminação infinita dividida pelo infinito dá 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Exercício 16

Resolva o limite pelo menos infinito da seguinte função:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Veja a solução

O numerador é um grau maior que o denominador, então o resultado da forma indeterminada ∞/∞ será infinito. Além disso, o sinal do infinito será negativo porque positivo entre negativo se traduz em negativo:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Exercício 17

Resolva o seguinte limite no infinito:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Veja a solução

A função exponencial é de ordem superior à função polinomial, então o limite dará infinito. Porém, dividindo o positivo pelo negativo, o sinal do infinito será negativo:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Exercício 18

Calcule o limite infinito da seguinte função com raiz quadrada:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

Veja a solução

O numerador é composto por uma raiz quadrada, portanto seu grau é 2/2=1. Então, o grau do numerador é igual ao do denominador, então a indeterminação infinita entre o infinito é resolvida da seguinte forma:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

Exercício 19

Resolva o limite infinito da seguinte função com dois radicais:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Veja a solução

O grau do numerador é 7/3=2,33 e o grau do denominador é 5/2=2,5. Portanto, como o grau do numerador é menor que o grau do denominador, o limite infinito indeterminado entre o infinito é 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Exercício 20

Calcule o seguinte limite:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Veja a solução

Independentemente do grau do numerador, como temos uma função exponencial no denominador, o resultado da forma indeterminada infinito sobre infinito é 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Exercício 21

Determine o limite infinito da seguinte função racional:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Veja a solução

Primeiro, tentamos calcular o limite substituindo o infinito na função:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Mas encontramos a indeterminação ∞ – ∞. Portanto, reduzimos as frações a um denominador comum:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

E como as duas frações agora têm o mesmo denominador, podemos combiná-las em uma única fração:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

Fazemos os parênteses do numerador:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

E finalmente, determinamos o limite:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

Neste caso a indeterminação ∞/∞ dá +∞ porque o grau do numerador é maior que o grau do denominador.

Exercício 22

Resolva o limite da seguinte função fracionária quando x se aproxima de 0:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Veja a solução

Primeiro tentamos calcular o limite normalmente:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Mas obtemos a forma indeterminada ∞-∞. Devemos, portanto, reduzir as frações da função a um denominador comum.

Neste caso, x ⁴ é um múltiplo de x ² , então simplesmente multiplicando o numerador e o denominador da segunda fração por x ² garantiremos que ambas as frações tenham o mesmo denominador:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Agora podemos subtrair as duas frações:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Tentamos resolver o limite novamente:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Mas acabamos com a indeterminação de uma constante começando do zero. É portanto necessário calcular os limites laterais da função.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

Concluindo, como os dois limites laterais da função no ponto x=0 dão -∞, a solução do limite é -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Exercício 23

Resolva o limite infinito da seguinte função com raízes:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Veja a solução

Tentando resolver o limite, obtemos a indeterminação infinito menos infinito:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Portanto, como existem radicais na função, ela deve ser multiplicada e dividida pela expressão radical conjugada:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

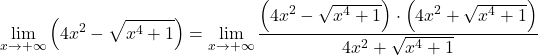
No numerador temos o produto notável de uma soma e uma diferença, que é igual à diferença dos quadrados. Ainda:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

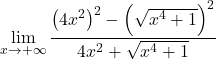
Simplificamos o radical ao quadrado:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

Operamos no numerador:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

E finalmente encontramos o limite:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

Neste caso o infinito indeterminado dividido pelo infinito é mais infinito porque o grau do numerador é maior que o grau do denominador (lembre-se que a raiz quadrada reduz o grau em dois:

$\sqrt{x^4} = x^{4/2} = x^2$

Exercício 24

Resolva o limite quando x se aproxima do infinito da seguinte função irracional:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Veja a solução

Primeiro, tentamos calcular o limite normalmente:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Mas isto resulta na indeterminação da diferença de infinitos. Portanto, como a função possui raízes, devemos multiplicar e dividir a expressão pelo radical conjugado:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

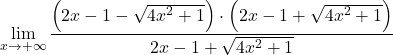
Agrupamos a igualdade notável do numerador da fração:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

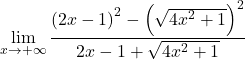
Resolvemos a raiz quadrada:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Resolvemos a identidade notável do quadrado de uma diferença:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Operamos no numerador:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

E finalmente calculamos o valor do limite no infinito:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Mesmo que haja um x ao quadrado no denominador, seu grau é na verdade 1 porque está dentro de uma raiz:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Portanto, o resultado da indeterminação -∞/+∞ é a divisão dos coeficientes do x de maior grau, pois o grau do numerador é igual ao grau do denominador.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Observe que, como existem dois termos de primeiro grau no denominador

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

, para resolver a indeterminação -∞/+∞ é necessário tomar todos os coeficientes dos termos de primeiro grau, ou seja, o

$2$

$2x$

e a

$\sqrt{4}$

$\sqrt{4x^2}.$

Exercício 25

Calcule o limite quando x se aproxima de 1 da seguinte função com frações:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

Veja a solução

Ao tentar fazer o limite obtemos o limite indeterminado do infinito menos infinito:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Devemos portanto reduzir as frações a um denominador comum, ou por outras palavras, devemos multiplicar o numerador e o denominador de uma fração pelo denominador da outra:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

E como agora as duas frações têm o mesmo denominador, podemos juntá-las:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Operamos:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

E tentamos resolver o limite novamente:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Mas encontramos a indeterminação zero dividida por zero. Devemos, portanto, fatorar os polinômios do numerador e do denominador:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Agora simplificamos a fração removendo o fator que se repete no numerador e no denominador:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

E finalmente, resolvemos o limite:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Limites ao infinito

Limite de uma função quando x tende ao infinito

Como resolver limites no infinito

Exemplos de limites ao infinito

Limites indeterminados ao infinito

Indeterminação infinita entre o infinito

Indeterminação infinita entre o infinito com raízes

Indeterminação infinita entre o infinito com funções exponenciais

Infinito menos indeterminação infinita

Indeterminação infinita menos infinita com frações

Indeterminação infinita menos infinita com raízes

Exercícios resolvidos sobre limites no infinito

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Exercício 7

Exercício 8

Exercício 9

Exercício 10

Exercício 11

Exercício 12

Exercício 13

Exercício 14

Exercício 15

Exercício 16

Exercício 17

Exercício 18

Exercício 19

Exercício 20

Exercício 21

Exercício 22

Exercício 23

Exercício 24

Exercício 25

Deixe um comentário Cancelar resposta