Neste artigo explicamos como resolver a indeterminação infinita menos infinita (∞-∞). Você encontrará exemplos dessa indeterminação com diversos tipos de funções e, além disso, poderá praticar com exercícios resolvidos passo a passo de indeterminação infinita menos infinita.
Resolvendo indeterminação infinita menos infinita
Quando o limite de uma função dá infinito menos infinito, significa que é uma indeterminação (ou uma forma indeterminada). Ou seja , o limite de uma função que dá indeterminação menos infinito não pode ser determinado realizando o cálculo direto, mas sim um procedimento preliminar deve ser realizado.
Portanto, para resolver a indeterminação infinita menos infinita, devemos primeiro aplicar um procedimento que depende do tipo de função: se for uma função polinomial, pode ser calculada por comparação, se for uma função racional, as frações devem ser reduzidas a um denominador comum e, se for uma função irracional, deve ser multiplicado pelo conjugado.
![]()
A seguir veremos com exemplos como a indeterminação infinito menos infinito é resolvida em cada tipo de função.
Indeterminação infinita menos infinita em funções polinomiais
Em um polinômio, a indeterminação infinito menos infinito é igual ao infinito de maior ordem, ou seja, o termo de maior ordem determina o sinal positivo ou negativo do infinito.
Por exemplo, observe o limite da seguinte função polinomial que fornece a forma indeterminada infinito menos infinito:
![]()
Neste caso, o termo x 2 é de segundo grau e o termo 3x é de primeiro grau, portanto o monômio x 2 é dominante por ser de ordem superior. Portanto, o resultado do limite é o infinito obtido deste termo.
Dê uma olhada nestes outros exemplos:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bfb5cd294a19de382f74738af6be724_l3.png)
Em suma, quando estabelecemos limites ao infinito em funções polinomiais , devemos simplesmente substituir o infinito no termo de maior grau , ignorando todos os outros termos.
Indeterminação infinita menos infinita com frações
Quando ocorre a indeterminação infinito menos infinito em uma adição ou subtração de frações algébricas , devemos primeiro fazer a adição ou subtração das frações e depois calcular o limite.
Vamos ver como calcular a indeterminação infinito menos infinito em uma função com frações resolvendo um exemplo passo a passo:
![]()
Vamos tentar calcular o limite primeiro:
![]()
Mas obtemos a indeterminação ∞-∞.
Então primeiro precisamos fazer a subtração de frações. Para isso, reduzimos as frações a um denominador comum, ou seja, multiplicamos o numerador e o denominador de uma fração pelo denominador da outra:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68e489c5833478cb20929ea07ae2971d_l3.png)
E agora que ambas as frações têm o mesmo denominador, podemos combiná-las numa única fração:
![]()
Operamos no numerador e no denominador:
![]()
E finalmente, calculamos o limite novamente:
![]()
Neste caso a indeterminação infinita entre o infinito dá +∞ porque o grau do numerador é maior que o grau do denominador.
➤ Veja: o que é o infinito entre o infinito?
indeterminação infinito menos infinito com raízes
Quando a indeterminação infinito menos infinito ocorre na adição ou subtração radical , devemos primeiro multiplicar e dividir a função pela expressão radical conjugada e, em seguida, resolver o limite.
Veremos como resolver a indeterminação infinito menos infinito em uma função irracional usando um exemplo passo a passo:
![]()
Vamos primeiro tentar resolver o limite da função com radicais:
![]()
No entanto, obtemos a forma indeterminada ∞-∞. Então, para saber quanto de indeterminação é infinito menos infinito, precisamos aplicar o procedimento explicado.
Como a função possui radicais, multiplicamos e dividimos toda a função pela expressão irracional conjugada:
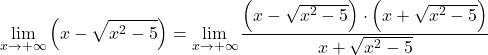
A expressão algébrica do numerador corresponde à identidade notável do produto de uma soma por uma diferença, podemos portanto simplificar a expressão:
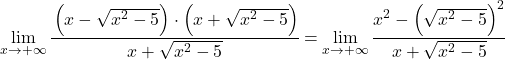
Agora simplificamos a raiz do limite, já que é elevado ao quadrado:
![]()
Operamos no numerador da fração:
![]()
![]()
E por fim, refazemos o cálculo do limite:
![]()
O resultado do limite é portanto 0, porque qualquer número dividido pelo infinito é igual a zero.
Resolvidos problemas de indeterminação infinita menos infinita
Exercício 1
Resolva o seguinte limite quando x se aproxima de mais infinito:
![]()
Neste limite, o termo de ordem mais elevada é de terceiro grau, por isso focamos no infinito obtido deste termo.
![]()
Exercício 2
Calcule o limite da seguinte função polinomial quando x se aproxima do infinito negativo:
![]()
O infinito negativo ao cubo permanece negativo, mas quando elevado ao quadrado torna-se positivo. mais tarde Embora seus sinais sejam modificados pelos coeficientes à sua frente:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-172f2927f65e61079b13abd02234f1c7_l3.png)
Então, a forma indeterminada infinito menos infinito é definida pelo termo de ordem mais alta (-5x 3 ), do qual obtemos infinito positivo:
![]()
Exercício 3
Determine o limite ao infinito da seguinte função racional:
![]()
Primeiro, tentamos calcular o limite substituindo o infinito na função:
![]()
Mas acabamos com a indeterminação ∞ – ∞. Portanto, reduzimos as frações a um denominador comum:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e2820674bc86d085f6deec7fdf9adf8_l3.png)
E como ambas as frações agora têm o mesmo denominador, podemos combiná-las em uma fração:
![]()
Fazemos os parênteses do numerador:
![]()
E, finalmente, determinamos o limite:
![]()
Neste caso a indeterminação ∞/∞ dá +∞ porque o grau do numerador é maior que o grau do denominador.
Exercício 4
Resolva o limite da seguinte função fracionária quando x se aproxima de 0:
![]()
Primeiro tentamos calcular o limite normalmente:
![]()
Mas obtemos a forma indeterminada ∞-∞. Portanto, precisamos reduzir as frações da função a um denominador comum.
Neste caso, x 4 é um múltiplo de x 2 , então simplesmente multiplicando o numerador e o denominador da segunda fração por x 2 obteremos que ambas as frações têm o mesmo denominador:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-876115dc1fb49e81373d70be5fdcfb5e_l3.png)
Agora podemos subtrair as duas frações:
![]()
Tentamos resolver o limite novamente:
![]()
Mas acabamos com a indeterminação de uma constante dividida por zero. É portanto necessário calcular os limites laterais da função.
![]()
![]()
Concluindo, como os dois limites laterais da função no ponto x=0 dão -∞, a solução do limite é -∞:
![]()
Exercício 5
Resolva o limite ao infinito da seguinte função com raízes:
![]()
Tentando resolver o limite, obtemos a indeterminação infinito menos infinito:
![]()
Portanto, como existem radicais na função, precisamos multiplicá-la e dividi-la pela expressão radical conjugada:
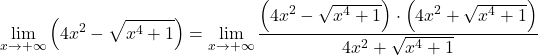
No numerador temos o produto notável de uma soma por uma diferença, que é igual à diferença dos quadrados. Ainda:
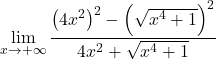
Simplificamos o radical ao quadrado:
![]()
Operamos no numerador:
![]()
![]()
E, finalmente, encontramos o limite:
![]()
Neste caso a indeterminação infinita dividida pelo infinito é mais infinita porque o grau do numerador é maior que o grau do denominador (lembre-se que a raiz quadrada reduz o grau em dois:
![]()
).
Exercício 6
Resolva o limite quando x se aproxima do infinito da seguinte função irracional:
![]()
Primeiro, tentamos calcular o limite normalmente:
![]()
Mas nos dá como resultado a indeterminação da diferença dos infinitos. Portanto, como a função possui raízes, precisamos multiplicar e dividir a expressão pelo radical conjugado:
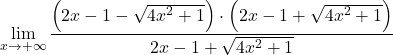
Agrupamos a igualdade notável do numerador da fração:
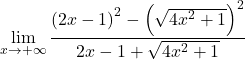
Resolvemos a raiz quadrada:
![]()
Resolvemos a identidade notável do quadrado de uma diferença:
![]()
Operamos no numerador:
![]()
![]()
E, por fim, calculamos o valor do limite no infinito:
![]()
Mesmo que haja um x ao quadrado no denominador, seu grau é na verdade 1 porque está dentro de uma raiz:
![]()
Portanto, o resultado da indeterminação -∞/+∞ é a divisão dos coeficientes do x de grau superior, pois o grau do numerador é igual ao grau do denominador.
![]()
Observe que, como existem dois termos de primeiro grau no denominador
![]()
E
![]()
, para resolver a indeterminação -∞/+∞ é necessário tomar todos os coeficientes dos termos de primeiro grau, ou seja, o
![]()
de
![]()
e a
![]()
de
![]()
Exercício 7
Calcule o limite quando x se aproxima de 1 da seguinte função com frações:
![]()
Tentando fazer o limite, obtemos o limite indeterminado do infinito menos infinito:
![]()
Devemos portanto reduzir as frações a um denominador comum, ou por outras palavras, devemos multiplicar o numerador e o denominador de uma fração pelo denominador da outra:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-75bf3ffa177f32711c5509ce5fe5992d_l3.png)
E como as duas frações agora têm o mesmo denominador, podemos juntá-las:
![]()
Operamos:
![]()
![]()
E tentamos resolver o limite novamente:
![]()
Mas encontramos a indeterminação zero dividida por zero. Devemos, portanto, fatorar os polinômios do numerador e do denominador:
![]()
Agora simplificamos a fração removendo o fator que se repete no numerador e no denominador:
![]()
E, finalmente, resolvemos o limite:
![]()