Identidades notáveis (ou produtos notáveis) -

Aqui você encontrará a explicação da resolução de todos os tipos de identidades notáveis (ou produtos notáveis). Você poderá ver quais são as fórmulas de todas as identidades notáveis, bem como exemplos e exercícios resolvidos passo a passo. Além disso, mostraremos para que servem essas famosas regras matemáticas.

👉👉 Abaixo explicamos cada identidade notável passo a passo, mas se preferir pode ir direto para a tabela 😉 onde todas as fórmulas estão resumidas . 👈👈

O que são identidades notáveis (ou produtos notáveis)?

Identidades notáveis , também chamadas de produtos notáveis ou igualdades notáveis , são regras matemáticas que permitem resolver diretamente operações com polinômios.

As fórmulas de identidade notáveis mais comuns são o quadrado de uma soma , o quadrado de uma diferença (ou subtração) e a soma vezes a diferença .

identidades ou igualdades de produtos notáveis

Mas a seguir não apenas ensinaremos como calcular esses produtos notáveis, mas também mostraremos todos os tipos de identidades notáveis que existem.

Fórmulas (ou produtos) de identidade notáveis

Depois de vermos a definição de produtos notáveis (ou igualdades notáveis), veremos quais são as fórmulas para identidades notáveis. Por outro lado, se você estiver interessado em demonstrações de fórmulas, poderá visualizá-las clicando nos botões “ver demonstração”.

quadrado de uma soma

O quadrado de uma soma , ou soma ao quadrado , é uma das principais identidades notáveis. Mais precisamente, é um binômio com dois termos positivos elevado a 2, ou seja, sua expressão algébrica é (a+b) ² .

Portanto, a fórmula do quadrado de uma soma é:

identidades notáveis ao quadrado com uma soma

Veja a demonstração da fórmula

Se partirmos de um binômio positivo elevado a 2:

$(a+b)^2$

Matematicamente, o quadrado acima é equivalente ao fator

$(a+b)$

multiplicado por si mesmo:

$(a+b)^2=(a+b)\cdot (a+b)$

Então, multiplicamos polinômios usando a propriedade distributiva:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Dos quatro termos obtidos,

$ab$

$ba$

parecem semelhantes para que possamos agrupá-los:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Tanto que já chegamos à expressão da fórmula da soma quadrada, da qual ela é derivada:

$(a+b)^2= a^2+2ab+b^2$

A título de curiosidade, o desenvolvimento da expressão para este tipo de produto notável é denominado trinômio quadrado perfeito.

De modo que o quadrado de uma soma é igual ao quadrado do primeiro termo, mais o dobro do produto do primeiro pelo segundo, mais o quadrado do segundo.

Portanto, para resolver uma soma quadrada, não basta elevar cada adição a ambas, mas, além disso, as duas adições devem ser multiplicadas entre si e por 2. É importante lembrar disso porque um erro muito típico deste tipo do produto É notável esquecer este termo.

identidades polinomiais e binomiais notáveis

Exemplo:

Calcule a seguinte identidade notável aplicando sua fórmula correspondente:

$(x+5)^2$

Como acabamos de ver, a fórmula para a igualdade notável de uma soma quadrada é:

$(a+b)^2=a^2+2ab+b^2$

Portanto, devemos primeiro identificar os parâmetros

$a$

$b$

da fórmula. Nesse caso,

$a$

representa o

$x$

do par e

$b$

corresponde ao número 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Então, agora que sabemos os valores de

$a$

e de

$b,$

podemos usar a fórmula de um binômio quadrado positivo para encontrar o resultado:

exemplos de identidades quadradas notáveis

quadrado de uma diferença

O quadrado de uma diferença , ou diferença ao quadrado , é outra das 3 identidades notáveis mais utilizadas. Em particular, corresponde a um binômio formado por um termo positivo e outro negativo elevado a 2, ou seja, sua expressão algébrica é (ab) ² .

Portanto, a fórmula do quadrado de uma diferença (ou quadrado de uma subtração) é a seguinte:

Veja a demonstração da fórmula

Da expressão binomial de uma subtração quadrada:

$(a-b)^2$

Obviamente, a potência anterior é igual ao produto do fator

$(a-b)$

multiplicado por si mesmo:

$(a-b)^2= (a-b)\cdot (a-b)$

Agora multiplicamos os dois parênteses aplicando a propriedade distributiva:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Então você só precisa agrupar termos semelhantes para finalizar a verificação da fórmula:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Então a fórmula do quadrado de uma diferença é provada matematicamente:

$(a-b)^2=a^2-2ab+b^2$

De modo que o quadrado de uma diferença é igual ao quadrado do primeiro termo, menos o dobro do produto do primeiro pelo segundo, mais o quadrado do segundo.

Quanto à notável igualdade da soma ao quadrado, não devemos esquecer de colocar o termo médio da fórmula, pois a seguinte equação está incorreta:

Exemplo:

Resolva a seguinte igualdade notável de uma diferença quadrada:

$(x-3)^2$

É o produto notável de uma subtração ao quadrado, portanto é necessário aplicar sua fórmula correspondente:

$(a-b)^2=a^2-2ab+b^2$

A seguir, devemos identificar quais são os valores das incógnitas.

$a$

$b$

da fórmula. Nesse caso,

$a$

é a variável

$x$

$b$

corresponde ao número 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Observe que o sinal negativo não faz parte do parâmetro

$b,$

mas você deve sempre pegar o número sem o sinal para aplicar corretamente esta fórmula.

Portanto, já conhecemos os valores de

$a$

e de

$b$

, é portanto suficiente substituir esses valores na fórmula para resolver a identidade notável:

exemplos e exercícios resolvidos passo a passo de igualdades notáveis

soma por diferença

O produto de uma soma e uma diferença é uma das 3 identidades notáveis mais utilizadas. Como o próprio nome sugere, é um binômio positivo multiplicado pelo seu binômio conjugado (mesmo binômio mas com o sinal intermediário alterado), ou seja, a expressão algébrica deste tipo de produto notável é (a +b) · (ab) .

A fórmula para a identidade notável do produto de uma soma por uma diferença é a seguinte:

identidades, produtos e igualdades notáveis das escolas secundárias 2, 3 e 4 que

Veja a demonstração da fórmula

Começando pelo produto de uma soma pela subtração de dois termos quaisquer:

$(a+b)\cdot (a-b)$

Para demonstrar a fórmula, basta multiplicar o primeiro parêntese pelo segundo parêntese usando a propriedade distributiva:

$\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}$

Agora agrupamos termos semelhantes:

$a^2 -ab+ba-b^2=a^2-b^2$

E conseguimos assim a expressão de uma igualdade notável. Assim é demonstrada a fórmula para este notável tipo de identidade:

$(a+b)\cdot (a-b) =a^2-b^2$

Assim, o produto da soma pela diferença de duas grandezas é igual à diferença dos quadrados dessas grandezas. Ou, por outras palavras, multiplicar a soma de dois termos diferentes subtraindo esses mesmos dois termos é equivalente a elevar ao quadrado cada um dos 2 termos e subtraí-los.

Exemplo:

Encontre, usando a fórmula correspondente, o seguinte produto notável da soma pela diferença de dois termos diferentes:

$(x+2)\cdot (x-2)$

Como vimos acima, a fórmula para a igualdade notável de uma soma multiplicada por uma diferença é a seguinte:

$(a+b)\cdot (a-b) =a^2-b^2$

Primeiramente o que precisamos fazer é identificar os valores das letras

$a$

$b$

da fórmula. Nesse caso

$a$

corresponde à variável

$x$

$b$

corresponde ao número 2.

$\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

E quando já sabemos quais valores os parâmetros assumem

$a$

$b,$

Aplicamos a fórmula do produto da soma pela diferença:

quadrado de um trinômio

O quadrado de um trinômio (polinômio formado por 3 termos) é igual ao quadrado do primeiro termo, mais o quadrado do segundo termo, mais o quadrado do terceiro termo, mais duas vezes o primeiro pelo segundo, mais duas vezes o primeiro pelo terceiro, mais o dobro do segundo pelo terceiro.

Quais são as fórmulas para todas as identidades, produtos ou igualdades notáveis?

Veja a demonstração da fórmula

De qualquer trinômio ao quadrado:

$(a+b+c)^2$

O quadrado acima pode ser fatorado no trinômio multiplicado por ele mesmo:

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Agora resolvemos a multiplicação polinomial:

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

E por fim, agrupamos termos semelhantes:

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

Desta forma, já chegamos à expressão da fórmula, então fica demonstrada a fórmula do quadrado de um trinômio:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Exemplo:

Encontre a seguinte igualdade notável:

$\left(x^2+x+3\right)^2$

A fórmula do quadrado de um trinômio é:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Como em todas as igualdades notáveis, primeiro você deve identificar os valores das incógnitas na fórmula. Neste exercício

$a$

Leste

$x^2,$

o coeficiente

$b$

corresponder ao

$x,$

$c$

é o termo independente 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

E quando já sabemos os valores, basta substituir esses valores na fórmula e fazer os cálculos:

calculadora de identidades, produtos e igualdades notáveis

Identidades (ou produtos) notáveis ao cubo

Acabamos de estudar todas as identidades notáveis ao quadrado, ou seja, todos os tipos de identidades notáveis que são formadas por potências elevadas a 2. Bom, agora vamos analisar as identidades notáveis ao cubo. É claro que as fórmulas de identidade ao cubo são um pouco mais complicadas, mas também são muito úteis.

cubo de uma soma

O notável produto cúbico de uma soma é um binômio (polinômio com apenas dois monômios) elevado a 3 cujos dois elementos são positivos. Portanto, algebricamente, o cubo de uma soma é expresso como (a+b) ³ .

A fórmula para a igualdade notável do cubo de uma soma é:

Quais são todos os produtos, identidades ou vínculos notáveis?

Veja a demonstração da fórmula

Partindo de um binômio positivo ao cubo:

$(a+b)^3$

A potência acima pode ser fatorada no produto do fator

$(a+b)$

pelo seu quadrado:

$(a+b)^3=(a+b)\cdot (a+b)^2$

Da mesma forma, como vimos em notáveis igualdades quadradas, o binômio

$(a+b)$

Pode ser resolvido com a fórmula do quadrado de uma soma:

$(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)$

Então multiplicamos os dois polinômios:

$\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}$

Finalmente, só temos que agrupar termos semelhantes:

$a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3$

E assim se verifica a fórmula para a identidade notável de uma soma binomial ao cubo:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Resumindo, uma soma elevada a 3 é igual ao cubo do primeiro, mais três vezes o quadrado do primeiro pelo segundo, mais três vezes o primeiro pelo quadrado do segundo, mais o cubo do segundo.

Exemplo:

Resolva a seguinte identidade notável de uma soma ao cubo usando sua fórmula correspondente:

$(x+2)^3$

Neste problema temos um binômio elevado a 3 cujos dois termos são positivos. Devemos, portanto, usar a fórmula para uma soma ao cubo:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Agora precisamos encontrar o valor dos parâmetros

$a$

$b$

da fórmula. Nesse caso,

$a$

corresponde à variável

$x$

$b$

é o número 2.

$\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Com o qual calculamos o produto notável substituindo os valores de

$a$

e de

$b$

na fórmula:

10 exemplos de produtos ou identidades notáveis

cubo de uma diferença

O cubo de uma diferença , ou cubo de uma subtração , é um binômio elevado a 3 que possui um termo com sinal negativo. Portanto, a expressão matemática para este notável tipo de produto é (ab) ³ .

A fórmula para o cubo de uma diferença (ou subtração) é:

identidades, produtos ou igualdades cúbicas notáveis

Veja a demonstração da fórmula

Obviamente, a prova desta fórmula é muito semelhante à do produto notável de uma soma ao cubo. Mas neste caso, partimos de um binômio cúbico negativo:

$(a-b)^3$

Claramente, a potenciação anterior pode ser decomposta no produto do fator

$(a-b)$

multiplicado pelo seu quadrado:

$(a-b)^3=(a-b)\cdot (a-b)^2$

Assim, como estudamos em identidades quadradas notáveis, o binômio

$(a-b)$

Pode ser calculado com a fórmula do quadrado da diferença:

$(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)$

Agora produzimos o produto dos dois polinômios:

$\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}$

E o último passo é agrupar termos semelhantes:

$a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3$

Assim se verifica a fórmula da identidade notável de um binômio subtraído elevado ao cubo:

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

Portanto, uma diferença (ou subtração) elevada a três é igual ao cubo do primeiro, menos três vezes o quadrado do primeiro pelo segundo, mais três vezes o primeiro pelo quadrado do segundo, menos o cubo do segundo.

Exemplo:

Calcule o próximo binômio ao cubo (diferença) usando sua fórmula correspondente:

$(3x-2)^3$

Neste exercício, temos um par com um elemento positivo e um elemento negativo. Devemos, portanto, usar a fórmula para uma diferença ao cubo:

$(a-b)^3 = a^3-3a^2b+3ab^2 -b^3$

Primeiro, como sempre, identificamos o valor das incógnitas

$a$

$b$

da fórmula. Nesse caso

$a$

representa o monômio

$3x$

$b$

é o termo independente do binômio, ou seja, 2.

$\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}$

Observe que o parâmetro

$b$

é simplesmente igual a 2, sem o sinal negativo do número. É importante ter isso em mente para aplicar corretamente a fórmula.

Finalmente, encontramos a identidade notável colocando os valores de

$a$

e de

$b$

na fórmula:

desenvolver identidades, produtos e igualdades notáveis

Tabela resumo de identidades notáveis

Em resumo, fizemos uma tabela com todas as identidades (ou produtos) notáveis que vimos, assim será mais fácil para você estudá-las. 😉

fórmulas de identidades ou igualdades de produtos notáveis

Exercícios resolvidos de identidades (ou produtos) notáveis

Para que você termine de entender a noção de identidades notáveis, também chamadas de produtos notáveis ou igualdades notáveis, preparamos diversos exercícios resolvidos passo a passo. Você pode tentar fazê-los e depois verificar se se saiu bem com as soluções dos exercícios.

⬇⬇ Não esqueça que você pode nos tirar todas as suas dúvidas abaixo nos comentários! ⬇⬇

Exercício 1

Expanda as seguintes identidades notáveis (soma de quadrados):

$\text{A)} \ (x+3)^2$

$\text{B)} \ (6x+2)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

veja solução

Todas as identidades notáveis no problema são somas quadradas, portanto neste caso devemos aplicar sempre a mesma fórmula:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Exercício 2

Desenvolva os seguintes produtos notáveis (diferenças ao quadrado):

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

veja solução

Todos os produtos notáveis neste exercício são subtrações ao quadrado, portanto só precisamos aplicar uma fórmula:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

Exercício 3

Desenvolva as seguintes igualdades notáveis (produtos de somas por diferenças):

$\text{A)} \ (x+5)(x-5)$

$\text{B)} \ (2x+6)(2x-6)$

$\text{C)} \ (x+7)(x-7)$

$\text{D)} \ (x-4y)(x+4y)$

veja solução

Como todas as igualdades notáveis neste exercício são multiplicações de somas por diferenças, todas elas são resolvidas com a mesma fórmula:

$(a+b)\cdot (a-b) =a^2-b^2$

$\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}$

$\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}$

$\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}$

$\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}$

Exercício 4

Resolva todas as seguintes identidades notáveis:

$\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)$

$\text{B)} \ \left(4x^2+2y^3\right)^2$

$\text{C)} \ \left(6x^3-4y^4\right)^2$

$\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)$

$\text{E)} \ \left(5x^2-9x\right)^2$

veja solução

$\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

$\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}$

$\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}$

Exercício 5

Calcule os seguintes produtos notáveis:

$\text{A)} \ (x+4)^3$

$\text{B)} \ \left(x^2-5\right)^3$

$\text{C)} \ \left(2x-1\right)^3$

$\text{D)} \ (5x+2)^3$

veja solução

Para encontrar todos os produtos notáveis do problema é necessário aplicar as fórmulas de soma e diferença ao cubo conforme os casos:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

$\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}$

Exercício 6

Resolva as seguintes igualdades notáveis:

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

veja solução

Para resolver todas essas identidades notáveis, precisamos usar a fórmula do quadrado de um trinômio, que é:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Exercício 7

Calcule as seguintes identidades notáveis com raízes e frações (alta dificuldade):

$\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

$\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)$

veja solução

A seção A) consiste em uma subtração ao quadrado, portanto para resolvê-la deve-se aplicar sua fórmula correspondente e, além disso, deve-se lembrar que se uma raiz for quadrada ela é simplificada:

$\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

A seção B) trata da adição por subtração e os monômios possuem coeficientes fracionários, com os quais este produto notável deve ser determinado usando a fórmula de adição por subtração e as propriedades das frações:

$\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}$

A notável igualdade na seção C) é uma soma elevada a 2 e, da mesma forma, é composta de frações. Portanto, para calculá-lo precisamos usar a fórmula da soma quadrada mais as propriedades das frações:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

A última identidade notável trata de uma soma vezes uma diferença com coeficientes irracionais, então aplicamos a fórmula para uma soma vezes uma diferença e depois simplificamos as raízes quadradas:

$\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}$

Outros tipos de identidade notáveis

Todas as identidades notáveis que discutimos acima são as mais comumente usadas. No entanto, em matemática existem outros tipos de produtos notáveis que também são interessantes de conhecer, pois são utilizados para diversos fins.

soma de cubos

A soma dos cubos corresponde a um binômio cujos dois termos são positivos e, além disso, suas raízes cúbicas são exatas. Portanto, a expressão algébrica para uma soma de cubos é a ³ +b ³ .

identidades, produtos ou vínculos notáveis resolvidos

A fórmula deste produto notável é utilizada para fatorar um polinômio, ou seja, através da fórmula transformamos um polinômio em produto de um binômio por um trinômio.

Para que você possa ver como isso é feito, aqui está um exemplo de aplicação desta notável identidade:

$x^3+8$

Na verdade, a expressão anterior consiste numa adição de cubos porque a raiz cúbica do monômio

$x^3$

é exato (não fornece número decimal) e o número 8 também:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{8} = 2$

$x^3+8=x^3+2^3$

Portanto, podemos usar a fórmula da soma de cubos perfeitos para transformar a expressão cúbica em produto de um binômio por um trinômio:

$a^3+b^3 = (a+b)(a^2-ab+b^2)$

$\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}$

diferença de cubos

A diferença (ou subtração) de cubos é um binômio composto por um termo positivo e um termo negativo cujas raízes cúbicas são exatas. Em outras palavras, uma diferença de cubos é expressa na forma a ³ -b ³ .

Exercícios resolvidos para fatorar polinômios com identidades notáveis

Vamos dar um exemplo para você ver como esse notável tipo de identidade é resolvido:

$x^3-27$

É uma diferença de cubos porque tanto a raiz cúbica do monômio

$x^3$

como 27 estão corretos:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{27} = 3$

$x^3-27=x^3-3^3$

Você pode, portanto, usar a fórmula da diferença de cubos perfeitos para fatorar o binômio:

$a^3-b^3 = (a-b)(a^2+ab+b^2)$

$\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}$

Produto de binômios com um termo comum

Este produto notável é usado para converter um produto de dois binômios que possuem um termo comum em um polinômio quadrático.

identidades, produtos ou igualdades notáveis pdf

Aqui está um exemplo elaborado deste tipo de produto notável:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

mais identidades

Embora as identidades notáveis sejam as mais famosas por serem as mais comuns, deve-se notar que também existem mais identidades com outros nomes. Aqui está uma lista de outras identidades menos conhecidas, caso você esteja curioso:

Identidades de Lagrange:

$(a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2$
$(a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2$

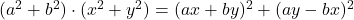
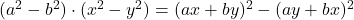
Identidades Legendre:

$(a+b)^2+(a-b)^2=2(a^2+b^2)$
$(a+b)^2-(a-b)^2=4ab$
$(a+b)^4-(a-b)^4=8ab(a^2+b^2)$

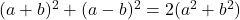
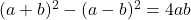
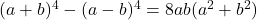
Identidade de Argand:

$(x^2+x+1)(x^2-x+1) = x^4+x^2+1$

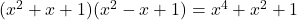
Identidades gaussianas:

$a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)$
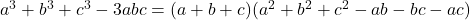
$a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]$

Aplicativos de identidade notáveis

Se você chegou até aqui, significa que já sabe fazer cálculos com identidades notáveis. Brilhante! Mas sério… para que servem as identidades notáveis? E quando são usadas identidades notáveis?

Como vimos ao longo deste artigo, o principal objetivo das identidades notáveis é simplificar os cálculos. Isto quer dizer que graças a produtos notáveis podemos resolver diretamente certas potências de polinômios complexos sem ter que realizar operações difíceis.

Mas igualdades notáveis também têm outras funções, como fatorar polinômios e completar quadrados. A seguir veremos em que consiste cada uma dessas aplicações.

Fatoração de polinômios

Alguns tipos muito específicos de polinômios podem ser fatorados com identidades notáveis. Por exemplo, se encontrarmos um polinômio composto por dois termos que são quadrados perfeitos (suas raízes quadradas são exatas), podemos fatorá-lo usando a notável fórmula de igualdade do produto de uma soma por uma diferença:

$a^2-b^2 =(a+b)(a-b)$

$x^2-9 =(x+3)(x-3)$

Da mesma forma, trinômios que respeitam as identidades notáveis do quadrado de uma adição ou subtração podem ser fatorados:

$a^2+2ab+b^2=(a+b)^2$

$x^2+4x+4=(x+2)^2$

$a^2-2ab+b^2=(a-b)^2$

$x^2-10x+25=(x-5)^2$

Da mesma forma, uma vez fatorado um polinômio, as raízes (ou zeros) desse polinômio podem ser encontradas. Mesmo assim, esse conceito é um pouco mais complicado de entender, então se você tiver mais interesse, recomendamos pesquisar a explicação no mecanismo de busca do nosso site (canto superior direito), pois temos um artigo completo explicando isso.

conclusão quadrada

Completar quadrados é um procedimento matemático usado para converter um trinômio quadrático na soma de um quadrado mais (ou menos) um número.

Dado qualquer trinômio:

$ax^2+bx+c$

Então o trinômio pode ser transformado na seguinte expressão:

$a(x+h)^2+k$

onde os parâmetros

$h$

$k$

são calculados com as seguintes fórmulas:

$h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2$

Mesmo que não lhe pareça, essas duas fórmulas são deduzidas de identidades notáveis. Assim, graças aos produtos notáveis, os quadrados podem ser completados.

Como exemplo, aplicaremos este procedimento ao seguinte trinômio:

$2x^2+4x+3$

Calculamos os parâmetros

$h$

$k:$

$h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1$

$k=c-ah^2 = 3-2\cdot 1^2 = 1$

E, portanto, o polinômio permanece:

$2(x+1)^2+1$

O que são identidades notáveis (ou produtos notáveis)?

Fórmulas (ou produtos) de identidade notáveis

quadrado de uma soma

Exemplo:

quadrado de uma diferença

Exemplo:

soma por diferença

Exemplo:

quadrado de um trinômio

Exemplo:

Identidades (ou produtos) notáveis ao cubo

cubo de uma soma

Exemplo:

cubo de uma diferença

Exemplo:

Tabela resumo de identidades notáveis

Exercícios resolvidos de identidades (ou produtos) notáveis

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Exercício 7

Outros tipos de identidade notáveis

soma de cubos

diferença de cubos

Produto de binômios com um termo comum

mais identidades

Aplicativos de identidade notáveis

Fatoração de polinômios

conclusão quadrada

Deixe um comentário Cancelar resposta