Aqui você encontrará tudo sobre a hipérbole: o que é, quais são seus elementos característicos, como encontrar sua equação, exemplos, exercícios resolvidos, etc.
O que é hipérbole?
A hipérbole é uma curva aberta com dois ramos, cuja definição matemática é a seguinte:
Na geometria analítica, uma hipérbole é o lugar geométrico dos pontos do plano que atende à seguinte condição: o valor absoluto da diferença nas distâncias entre qualquer ponto da hipérbole e dois pontos fixos (chamados focos) deve ser constante.
Além disso, o valor da subtração destas duas distâncias é sempre equivalente à distância entre os dois vértices da hipérbole.
![]()

Abaixo veremos o que significa o coeficiente
![]()
de uma hipérbole.
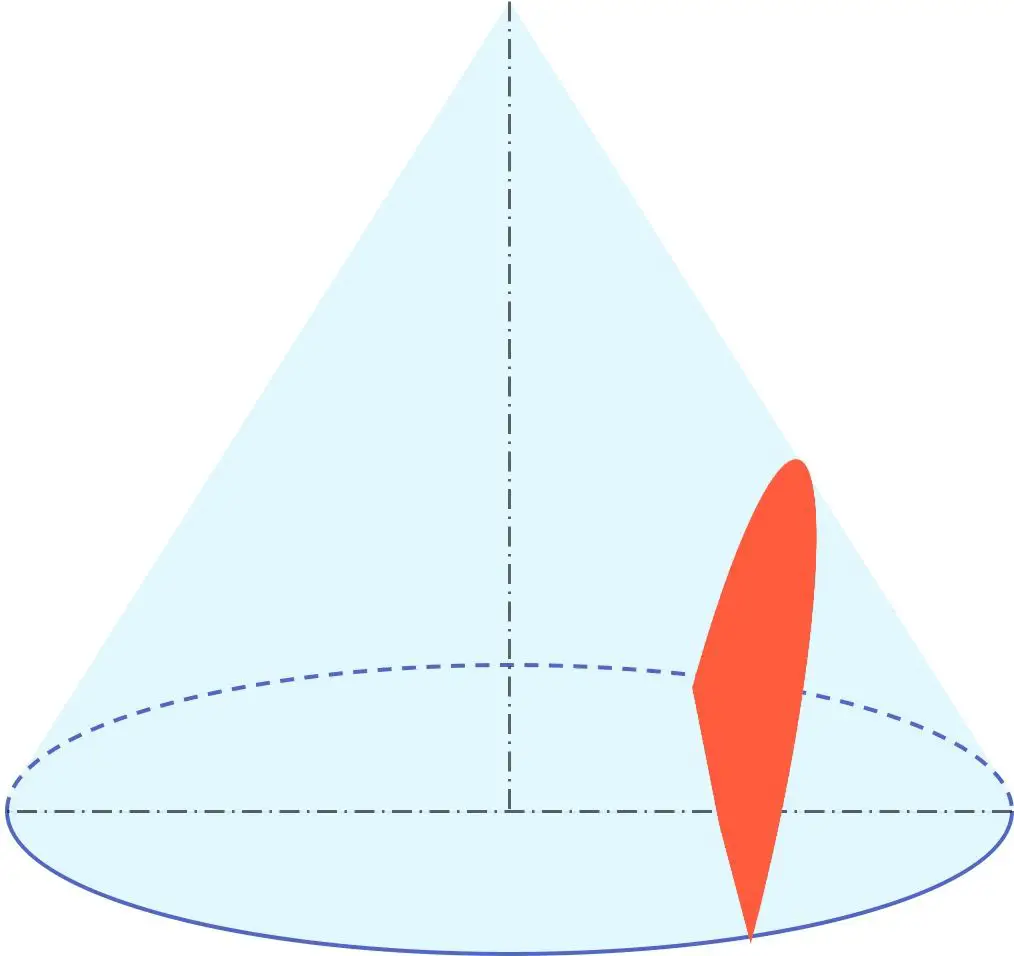
Além disso, a hipérbole faz parte do grupo geométrico denominado cônicas junto com a circunferência, a elipse e a parábola. Portanto, uma hipérbole é uma seção cônica, ou seja, pode ser obtida a partir de um cone.
Em particular, uma hipérbole é o resultado da seção de um cone por um plano com ângulo menor que o ângulo formado pelo gerador do cone em relação ao seu eixo de revolução.
Elementos de uma hipérbole
As características de uma hipérbole dependem do seguinte:
- Os focos : são dois pontos fixos característicos de cada hipérbole (pontos F e F’ no gráfico abaixo). O valor absoluto da diferença entre as distâncias de qualquer ponto da hipérbole a cada foco é constante e igual a

- Eixo focal ou principal : é a reta que passa pelos dois focos da hipérbole. Corresponde a um eixo de simetria da referida figura geométrica. Também chamado de eixo transversal ou transversal.
- Eixo secundário : é a bissetriz do segmento FF’ (reta que passa pelos pontos B e B’). Além disso, é uma linha perpendicular ao eixo focal e é outro eixo de simetria da hipérbole
- Centro (O) : é o ponto de intersecção dos dois eixos e o ponto médio dos dois vértices e dos dois focos. Como a hipérbole tem dois eixos de simetria, ela também é o centro de simetria.
- Vértices (A e A’) : são os pontos de intersecção dos ramos da hipérbole com o eixo focal.
- Raios vetoriais (R) : são os segmentos que vão de qualquer ponto da hipérbole até cada foco.
- Distância focal : é o comprimento do segmento composto entre os dois focos.
- Eixo maior ou eixo real: é o segmento que vai do ponto A ao ponto A’, seu comprimento equivale a

- Eixo pequeno ou eixo imaginário: é o segmento que vai do ponto B ao ponto B’, seu comprimento equivale a
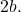
- Assíntotas : são as linhas pontilhadas mostradas no gráfico. Veremos a seguir como eles são calculados.
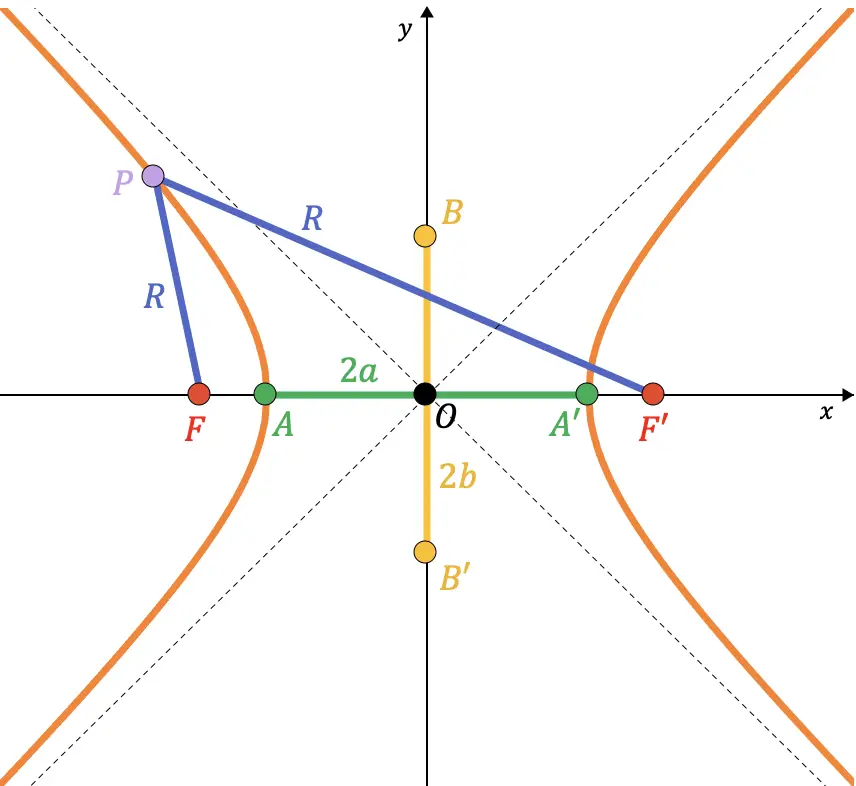
Relação entre os elementos de uma hipérbole
Em primeiro lugar, dizemos que semieixo significa metade de um eixo. Por exemplo, o semieixo verdadeiro é o segmento que vai do ponto A ao centro da hipérbole, cujo comprimento é
![]()
Assim, existe uma relação muito importante entre o semieixo real, o semieixo imaginário e a meia distância focal. Na verdade, a fórmula que vamos deduzir a seguir é muito utilizada para resolver exercícios e problemas de hipérbole.
Você deve saber que os pontos B e B’ de uma hipérbole correspondem aos pontos de intersecção do eixo principal e do círculo imaginário de raio
![]()
(distância semifocal) do centro ao ponto A. Portanto, como você pode ver na representação gráfica a seguir, o segmento que une o ponto A e o ponto B coincide com o raio do referido círculo (
![]()
):
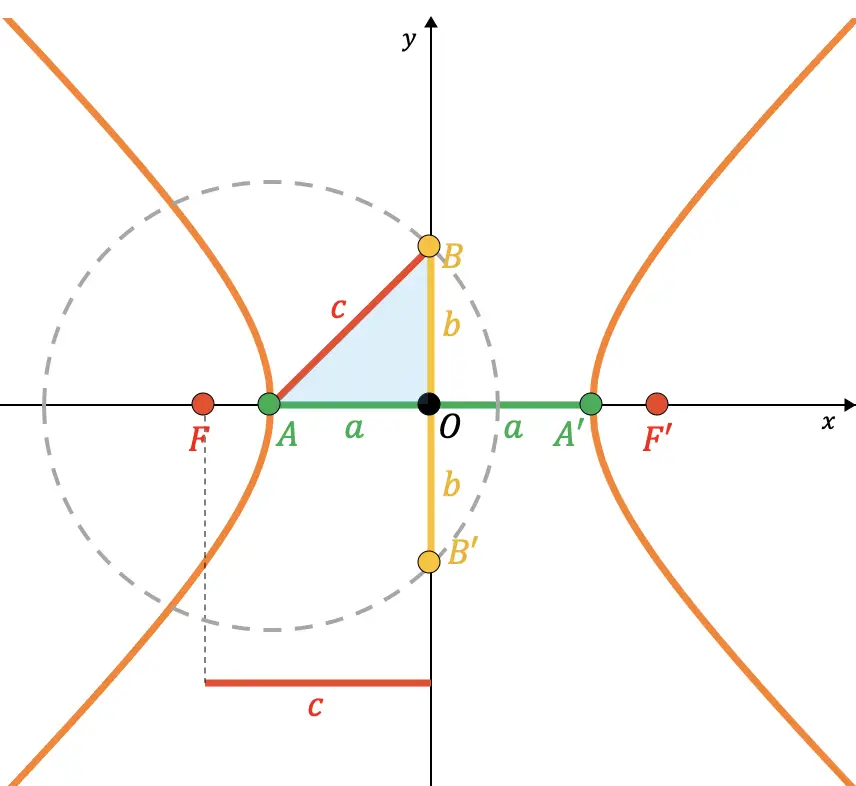
Portanto, pode ser demonstrado a partir do teorema de Pitágoras que a relação entre os parâmetros
![]()
E
![]()
é o seguinte:
![]()
equação da hipérbole
Existem vários tipos de equações de hipérbole, pois dependendo de suas propriedades uma ou outra é utilizada para expressá-la matematicamente. A seguir, analisaremos cada um detalhadamente.
Primeiro, temos a equação ordinária da hipérbole. Em segundo lugar, veremos uma variante da equação ordinária, esta é a equação reduzida ou canônica da hipérbole. A seguir, estudaremos como é a equação geral de uma hipérbole. E por fim, analisaremos as equações de dois casos especiais de hipérboles: a hipérbole equilátera e as hipérboles conjugadas .
Equação ordinária da hipérbole
Quando queremos definir por uma equação uma hipérbole com centro exterior na origem das coordenadas (ponto (0,0)), devemos utilizar a seguinte fórmula:
A fórmula para a equação ordinária da hipérbole em coordenadas cartesianas é a seguinte:
![]()
Ouro:
-

E

são as coordenadas do centro da hipérbole:
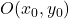
-

é o comprimento do semieixo maior da hipérbole.
-

é o comprimento do semieixo menor da hipérbole.
Com esta equação você pode descrever hipérboles cujo eixo focal é horizontal (ramos abertos para a esquerda e para a direita), que é o que normalmente são as hipérboles. Mas se trabalharmos com um eixo focal vertical (ramos abertos de cima para baixo), o sinal negativo passa da variável y para a variável x :
![]()
Ouro
![]()
E
![]()
são, como antes, as coordenadas do centro da hipérbole e os termos
![]()
E
![]()
eles ainda são o semieixo maior e o semieixo menor da hipérbole, embora, ao contrário de antes, estes dois agora serão orientados verticalmente e horizontalmente, respectivamente.
Equação canônica ou reduzida da hipérbole
Este tipo de equação de hipérbole é muito semelhante à equação ordinária, a única diferença é que a equação canônica é usada para expressar analiticamente hipérboles cujo centro é o ponto (0,0). Portanto, utilizamos a equação canônica ou reduzida da hipérbole quando o centro da hipérbole é a origem das coordenadas.
Deduziremos agora a fórmula para a equação reduzida da hipérbole a partir de sua equação ordinária:
![]()
Se o centro da hipérbole for a origem das coordenadas, ou seja, o ponto (0,0), o seguinte será sempre verdadeiro:
![]()
![]()
Assim, a fórmula da equação canônica ou reduzida da hipérbole será:
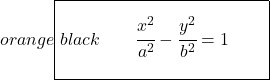
Como antes, se o eixo focal fosse vertical em vez de horizontal, a variável negativa seria x :
![]()
Equação geral da hipérbole
A fórmula para a equação geral de uma hipérbole é a seguinte:
![]()
No entanto, para que a equação acima seja uma hipérbole, os coeficientes
![]()
E
![]()
Devem ser diferentes de zero e, ao mesmo tempo, ter sinal oposto.
Equação da hipérbole equilátera
Uma hipérbole equilátera é uma hipérbole em que o comprimento do semieixo real é equivalente ao comprimento do semieixo imaginário, isso significa que
![]()
Portanto, a equação de uma hipérbole equilátera é:
![]()
Além disso, as assíntotas das hipérboles equiláteras são perpendiculares entre si. E as equações dessas retas são as seguintes:
![]()
![]()
Se olharmos com atenção, essas duas equações são as bissetoras do primeiro (e terceiro) quadrante e do segundo (e quarto) quadrante, respectivamente. Portanto, se girarmos uma hipérbole equilátera 45° para a esquerda, suas assíntotas ocuparão o lugar dos eixos coordenados:
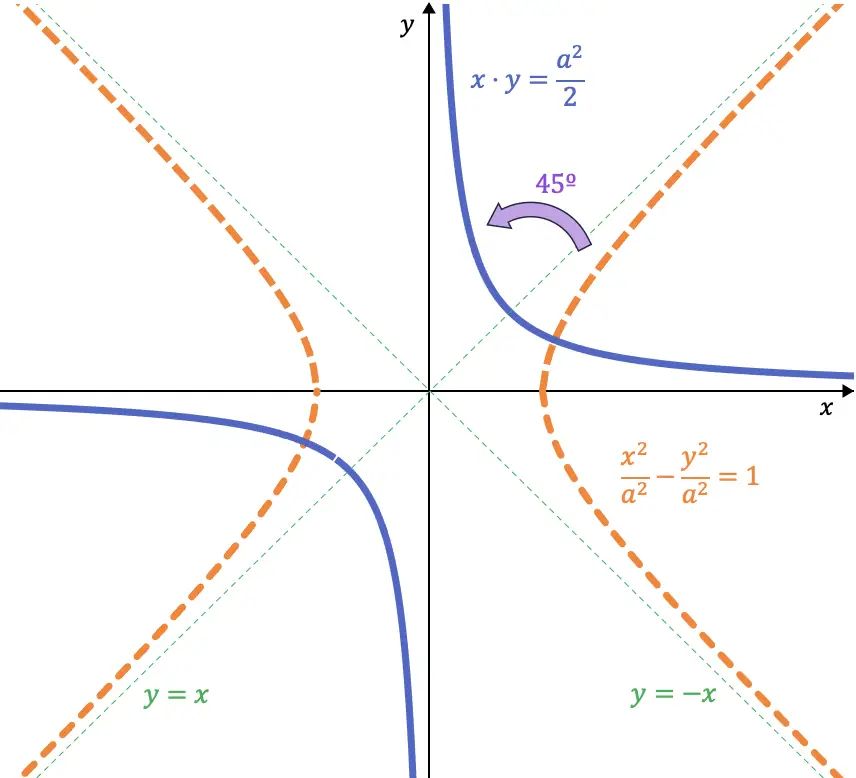
Então, quando fazemos a volta de 45º, a equação da hipérbole é:
![]()
hipérboles conjugadas
Duas hipérboles são conjugadas se o eixo real de uma for equivalente ao eixo imaginário da outra . Portanto, a única diferença entre as equações de duas hipérboles conjugadas é qual variável é negada, pois os coeficientes dos denominadores devem permanecer os mesmos.
Aqui está um exemplo das equações de duas hipérboles conjugadas entre si:
![]()
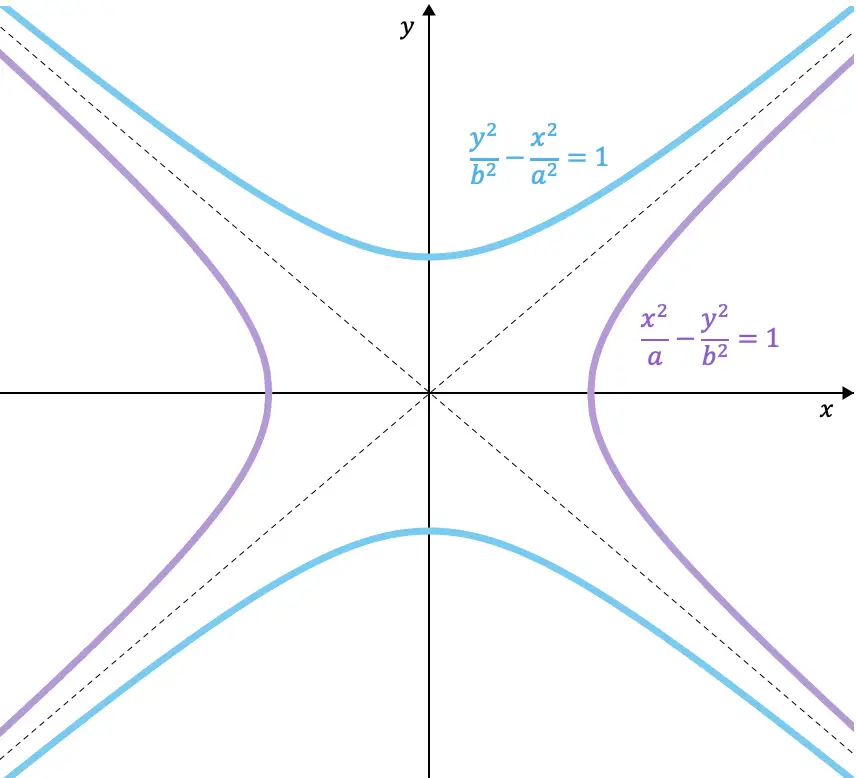
Além disso, como você pode ver nas hipérboles representadas graficamente, as hipérboles conjugadas compartilham as mesmas assíntotas.
Assíntotas da hipérbole
Como você viu nos gráficos anteriores, cada hipérbole possui duas assíntotas. Lembre-se de que uma assíntota é uma linha reta que se aproxima muito de uma função, mas nunca a intercepta ou a toca.
Assim, as fórmulas que correspondem às assíntotas das hipérboles são:
![]()
![]()
Para que as assíntotas de qualquer hipérbole possam ser facilmente determinadas usando seus coeficientes
![]()
E
![]()
que são respectivamente os comprimentos do semieixo real e do semieixo imaginário da hipérbole.
Excentricidade da hipérbole
A excentricidade de uma hipérbole é um parâmetro característico que determina quão aberta ou fechada ela é. Numericamente, a excentricidade de uma hipérbole é calculada dividindo sua meia distância focal por seu semieixo real:
![]()
A excentricidade de qualquer hipérbole é sempre maior que 1:
Finalmente, deve-se notar que a excentricidade de uma hipérbole equilátera é sempre igual a
![]()
Problemas de hipérbole resolvidos
Abaixo você pode praticar os conceitos que vimos com problemas e exercícios resolvidos de hipérboles e da equação da hipérbole.
Exercício 1
Qual é a equação da hipérbole com centro no ponto (-1,3), comprimento do semieixo real de 3 unidades e comprimento do semieixo imaginário (paralelo ao eixo Y) de 7 unidades?
Para encontrar a equação da hipérbole, basta aplicar a fórmula da equação ordinária da hipérbole:
![]()
Substituímos as coordenadas do centro da hipérbole na equação:
![]()
![]()
E por fim, substituímos os valores das incógnitas
![]()
E
![]()
![]()
![]()
Exercício 2
Encontre as coordenadas do centro, dos vértices, dos focos, do valor da excentricidade e das assíntotas da hipérbole cuja equação é definida por:
![]()
Em primeiro lugar, deve-se notar que a variável negativa na equação é a variável y , portanto os ramos da hipérbole se abrirão para a direita e para a esquerda (eixo focal paralelo ao eixo X).
Em segundo lugar, a equação corresponde à equação canônica (ou reduzida) da hipérbole, portanto seu centro é a origem das coordenadas.
![]()
Uma vez conhecido o centro da hipérbole, para calcular todo o resto precisamos encontrar o valor do semieixo real (parâmetro
![]()
) e o semieixo imaginário (parâmetro
![]()
). Podemos deduzir ambos da fórmula da equação canônica (ou reduzida) da hipérbole:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Portanto, se existe uma distância de 5 unidades entre o centro e os vértices, isso implica que os vértices das hipérboles são:
![]()
Para determinar as coordenadas de cada ponto focal, você deve saber o valor da meia distância focal (parâmetro
![]()
). E, para isso, podemos utilizar a fórmula que liga os elementos de uma hipérbole:
![]()
![]()
![]()
Existe, portanto, um espaço de 13 unidades entre o centro e as residências. Assim, as coordenadas de cada domicílio são:
![]()
Então, para calcular a excentricidade da hipérbole, precisamos usar sua fórmula correspondente:
![]()
E, por fim, encontramos as assíntotas da hipérbole com suas fórmulas:
![]()
![]()
Exercício 3
Calcule a equação da hipérbole com centro na origem das coordenadas sabendo que a diferença nas distâncias de um ponto da hipérbole aos focos F(-4,0) e F(4,0) é de 6 unidades.
Primeiramente, como a hipérbole tem centro na origem das coordenadas, usaremos a equação canônica ou reduzida:
![]()
Então, de acordo com a definição de hipérbole, o valor absoluto da diferença das distâncias de um de seus pontos aos focos (que neste caso é 6) deve ser igual ao comprimento do eixo real (
![]()
). Ainda:
![]()
![]()
![]()
![]()
Por outro lado, o centro da hipérbole é o ponto (0,0) e o foco é o ponto (4,0). Para que a distância aos dois pontos (parâmetro
![]()
) são 4 unidades.
![]()
Agora podemos saber o valor do parâmetro
![]()
com a relação matemática entre os 3 coeficientes característicos da hipérbole:
![]()
![]()
![]()
![]()
Portanto, a equação da hipérbole é:
![]()
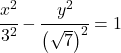
![]()