Nesta página você encontrará uma explicação do que é um plano, como ele é calculado e todas as suas propriedades. Além disso, você poderá ver exemplos de planos, quais são as posições relativas entre dois planos, como determinar o ângulo entre 2 planos e, por fim, como expressar numericamente qualquer plano usando as equações dos planos.
O que é um plano?
Na geometria analítica, a definição do plano é a seguinte:
Um plano é um objeto geométrico que possui duas dimensões (comprimento e largura).
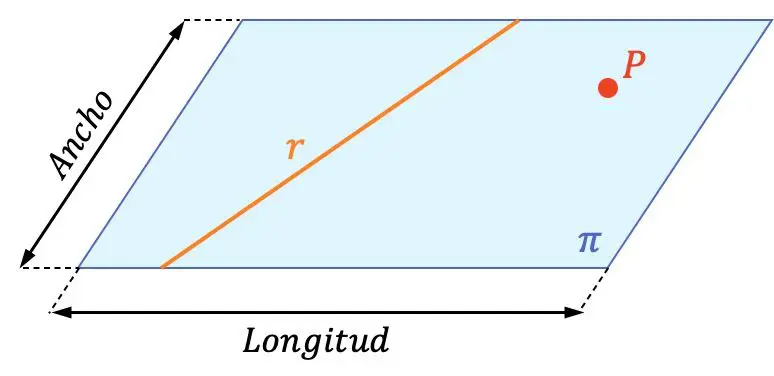
Portanto, um plano contém infinitas retas e infinitos pontos. Na representação gráfica acima você pode ver a diferença entre um plano, uma linha e um ponto. Você também pode verificar se a linha
![]()
e a dica
![]()
estão contidos no plano
![]()
Como você pode ver no plano gráfico, os planos geralmente são nomeados com letras gregas:
![]()
Um exemplo de plano que usamos muito em matemática é o plano cartesiano. O plano cartesiano é o plano definido pelo eixo das abscissas (eixo X) e pelo eixo das ordenadas (eixo Y). Um dos usos do plano cartesiano é que ele é usado para descrever a posição de um objeto em um sistema de referência.
Determinando um plano
Agora que vimos o significado de plano, vamos ver como qualquer plano no espaço tridimensional (em R3) pode ser determinado.
Um plano é inteiramente determinado pelos seguintes elementos geométricos:
- Três pontos não alinhados.
- Uma linha reta e um ponto externo.
- Duas linhas paralelas ou duas linhas que se cruzam.
Em relação ao último ponto, você provavelmente já sabe o que significa duas retas serem paralelas. Mas o significado das retas secantes é menos conhecido, então se você tiver alguma dúvida aqui, você pode conferir o que são retas secantes .
Portanto, se tivermos alguma das 3 condições anteriores, significa que podemos traçar um plano.
propriedades do plano
O plano atende às seguintes características:
- Um plano contém uma infinidade de pontos.
- Um plano contém uma infinidade de linhas.
- Um plano é ilimitado, ou seja, é uma superfície que se estende no espaço sem limites.
- Dois planos que se cruzam determinam uma linha.
- Uma reta que tem um ponto em um plano não está necessariamente contida nele. Para que uma reta faça parte de um plano, ela deve ter pelo menos dois pontos no plano.
- Planos infinitos cruzam uma linha reta.
- Um semiplano é cada uma das 2 partes em que um plano é dividido quando é cortado por uma de suas linhas.
equações planas
Na geometria analítica, a equação de um plano é uma equação que permite que qualquer plano seja expresso matematicamente. Então, para encontrar a equação de um plano, você só precisa de um ponto e dois vetores linearmente independentes pertencentes a esse plano.

Porém, como vimos acima na explicação do conceito de plano, existem diversas formas de determinar um plano. Bem, da mesma forma, também existem diferentes maneiras de expressar analiticamente um plano.
Assim todos os tipos de equações do plano são: a equação vetorial , as equações paramétricas , a equação implícita (ou geral) e a equação canônica (ou segmental) do plano.
A seguir veremos detalhadamente a explicação e fórmula de todas as equações do plano.
Equação vetorial do plano
Considere um ponto e dois vetores de direção de um plano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
A fórmula para a equação vetorial de um plano é:
![]()
Ou equivalente:
![]()
Ouro
![]()
E
![]()
são dois escalares, ou seja, dois números reais.
Equações paramétricas do plano
A fórmula para a equação paramétrica de um plano é:
![]()
Ouro:
-
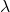
E
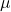
são dois escalares, ou seja, dois números reais.
-
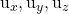
são os componentes de um dos dois vetores norteadores do plano
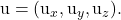
-
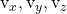
são os componentes do outro vetor diretor do plano
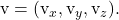
Equação implícita ou geral do plano
Considere um ponto e dois vetores de direção de um plano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
A equação implícita, geral ou cartesiana de um plano é obtida resolvendo o seguinte determinante e igualando o resultado a 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Assim, a equação implícita ou geral do plano resultante será a seguinte:
![]()
Este tipo de equação plana também é chamada de equação plana cartesiana.
Equação canônica ou segmentar do plano
A fórmula para a equação canônica ou segmentar de um plano é a seguinte:
![]()
Ouro:
-

é o ponto de intersecção entre o plano e o eixo X.
-

é o ponto de intersecção entre o plano e o eixo Y.
-

É aqui que o plano cruza o eixo Z.
A equação canônica (ou equação segmental) do plano também pode ser obtida a partir de sua equação geral:
![]()
Primeiro, resolvemos o coeficiente D da equação:
![]()
Em seguida, dividimos toda a equação do plano pelo valor do parâmetro D com sinal alterado:
![]()
![]()
E, utilizando as propriedades das frações, chegamos à seguinte expressão:
![]()
Deduzimos, portanto, desta expressão as fórmulas que permitem calcular diretamente os termos da equação canônica ou segmentar de um plano:
![]()
conseqüentemente, para poder formar esta variante das equações do plano, os coeficientes A, B e C devem ser diferentes de zero, evitando assim indeterminações das frações.
Posição relativa de dois planos
Na geometria analítica, existem apenas três posições relativas possíveis entre dois planos: planos secantes, planos paralelos e planos coincidentes.
- Planos que se cruzam : Dois planos estão se cruzando se eles se cruzarem apenas em uma linha.
- Planos paralelos : Dois planos são paralelos se não se cruzam em nenhum ponto.
- Planos Coincidentes : Dois planos são coincidentes se todos tiverem pontos em comum.
planos que se cruzam

planos paralelos

planos coincidentes

Além disso, se dois planos que se cruzam se cruzam em um ângulo de 90º, são dois planos perpendiculares entre si .
Ângulo entre dois planos
O ângulo entre dois planos é igual ao ângulo formado pelos vetores normais desses planos. Portanto, para encontrar o ângulo entre dois planos, calcula-se o ângulo formado por seus vetores normais, uma vez que são equivalentes.
Então, uma vez que sabemos exatamente em que consiste o ângulo entre dois planos, vamos ver a fórmula para calcular o ângulo entre dois planos no espaço, que é deduzida da fórmula do ângulo entre dois vetores:
Dada a equação geral (ou implícita) de dois planos diferentes:
![]()
![]()
O vetor normal de cada plano é:
![]()
![]()
E o ângulo formado por esses dois planos é determinado calculando o ângulo formado por seus vetores normais usando a seguinte fórmula:
![]()
Obviamente, uma vez calculado o cosseno do ângulo formado pelos dois planos a partir da fórmula, devemos inverter o cosseno para encontrar o valor desse ângulo.
Por outro lado, quando os dois planos são perpendiculares ou paralelos, não é necessário aplicar a fórmula, pois o ângulo entre os 2 planos pode ser determinado diretamente:
- O ângulo entre dois planos paralelos é 0º, pois seus vetores normais têm a mesma direção.
- O ângulo entre dois planos perpendiculares é 90º, porque seus vetores normais também são perpendiculares (ou ortogonais) entre si e, portanto, formam um ângulo reto.