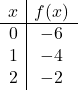Funções de valor absoluto -

Esta página explica o que é uma função de valor absoluto. Você também aprenderá como definir uma função de valor absoluto por partes e como representar esses tipos de funções em um gráfico. Além disso, você verá exemplos de funções de valor absoluto e poderá praticar com exercícios e problemas resolvidos passo a passo.

O que são funções de valor absoluto?

A definição de uma função de valor absoluto é a seguinte:

O valor absoluto de uma função transforma todas as suas imagens em imagens positivas. Portanto, o caminho de uma função absoluta nunca pode ter valores negativos.

A função a seguir é um exemplo de função de valor absoluto:

$f(x)=\lvert 5x \rvert$

Se ao avaliar a função em um ponto obtivermos um resultado positivo, ele permanece positivo:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Por outro lado, se o resultado for negativo torna-se positivo:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Funções de valor absoluto geralmente são dadas no ensino médio, pois suas características as tornam um pouco difíceis de entender.

Como definir por partes uma função com um valor absoluto

Uma função de valor absoluto pode ser expressa como uma função por partes. Para fazer isso, você deve alterar o sinal da função nos intervalos que é negativo.

Vejamos um exemplo de como passar de uma função de valor absoluto para uma função por partes:

Expresse a seguinte função com um valor absoluto como uma função por partes:

$f(x) = \lvert 4 - x^2 \rvert$

A primeira coisa que precisamos fazer é determinar quando a função é negativa. Para fazer isso, definimos a expressão algébrica em valor absoluto igual a 0 e resolvemos a equação:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Representamos agora os valores obtidos na reta:

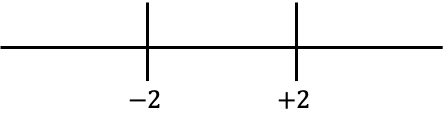
E olhamos qual sinal tem a função sem o valor absoluto em cada intervalo da reta:

$x<-2$

Tomamos qualquer ponto menor que -2, por exemplo

$x=-3:$

$4-(-3)^2$

$-5$

Negativo

$-2 < x < 2$

Tomamos qualquer ponto entre -2 e +2, por exemplo

$x=0:$

$4-0^2$

$+4$

Positivo

$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> Por exemplo, tomamos qualquer ponto maior que 2 <p class=$ $x=3:$

$4-3^2$

$-5$

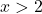
Negativo

Como vimos, a função sem o valor absoluto seria negativa nos intervalos

$x<-2$

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> Portanto, precisamos expressar a função em travessões alterando seu sinal nestes intervalos: 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> Observe que em alguns intervalos você deve incluir igualdade. Por exemplo, aqui colocamos no segundo intervalo <p class=$ $-2 \le x \le 2$

. Mas você pode colocá-lo em qualquer intervalo que desejar desde que haja empate em todos os pontos críticos. Em outras palavras, seria a mesma coisa se tivéssemos definido a função da seguinte forma:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Como representar uma função com valor absoluto

Para representar uma função com valor absoluto em um gráfico, precisamos seguir os passos descritos abaixo:

Represente a função como se ela não tivesse valor absoluto.
Nos intervalos em que a função é negativa, ou seja, fica abaixo do eixo X, desenhe a função simétrica.
Exclua a parte da função que está abaixo do eixo X.

Vamos ver um exemplo de como representar graficamente uma função com valor absoluto

Faça um gráfico da seguinte função em valor absoluto:

$f(x) = \lvert -x+2 \rvert$

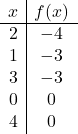
Para representar uma função com valor absoluto, devemos primeiro representar a função sem valor absoluto. Fazemos, portanto, a tabela de valores da função sem o valor absoluto:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

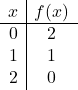
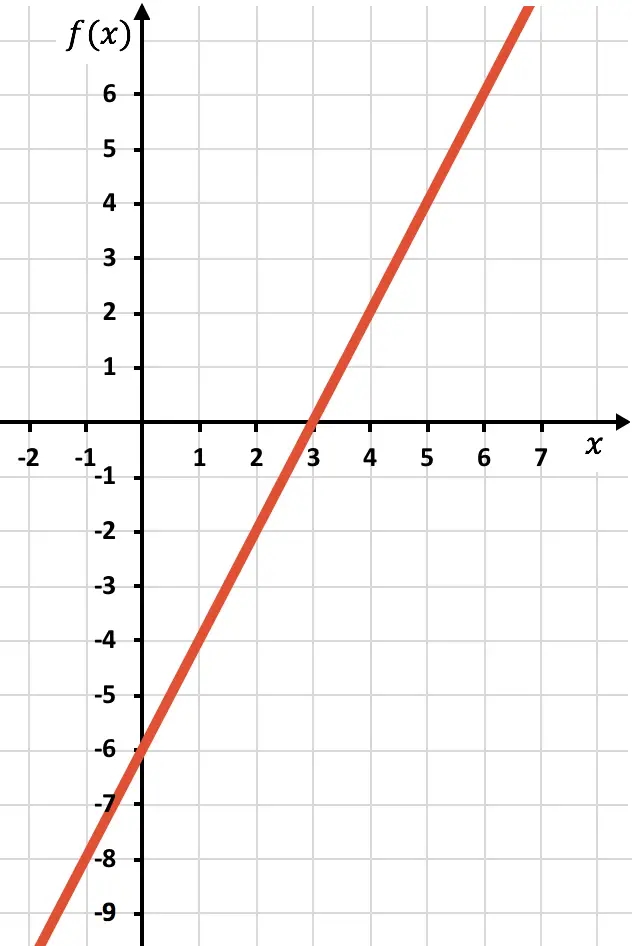
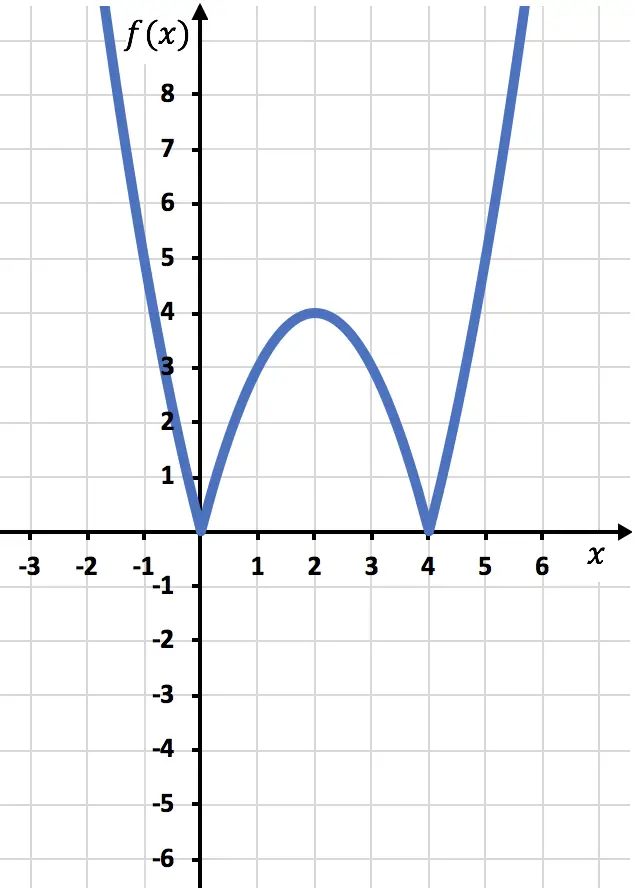
Representamos graficamente os pontos e desenhamos a reta como se fosse uma função normal:

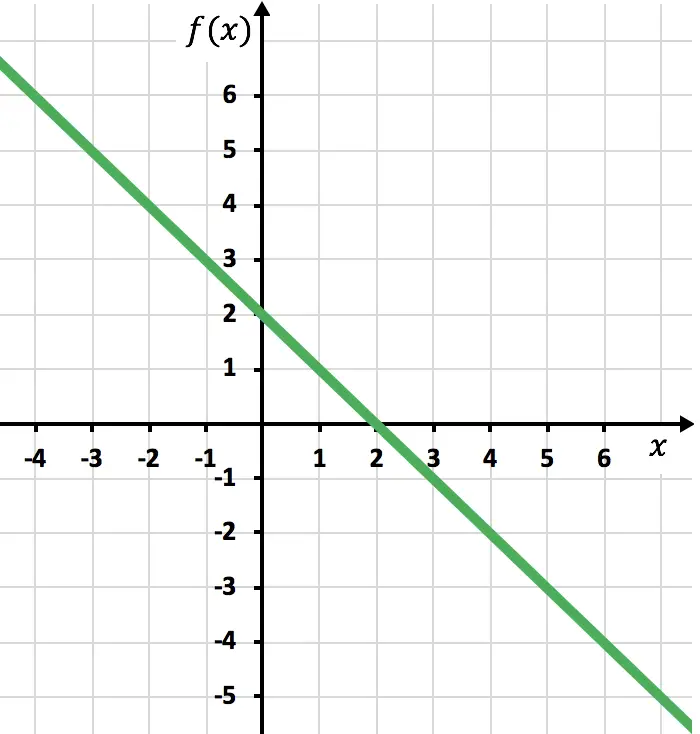
Agora precisamos desenhar a função simétrica onde a função é negativa, ou seja, onde está abaixo do eixo x. Portanto, invertemos a função a partir de x=2:

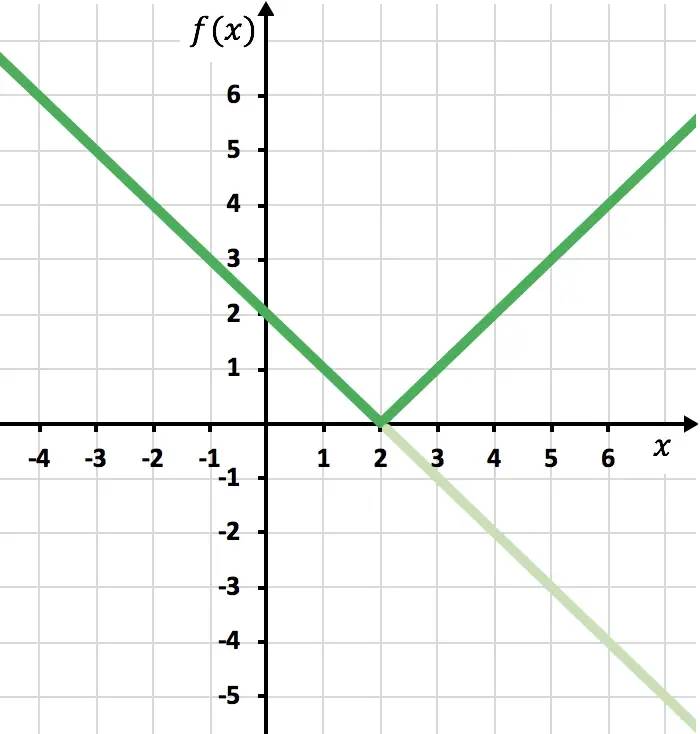
como representar uma função com um valor absoluto

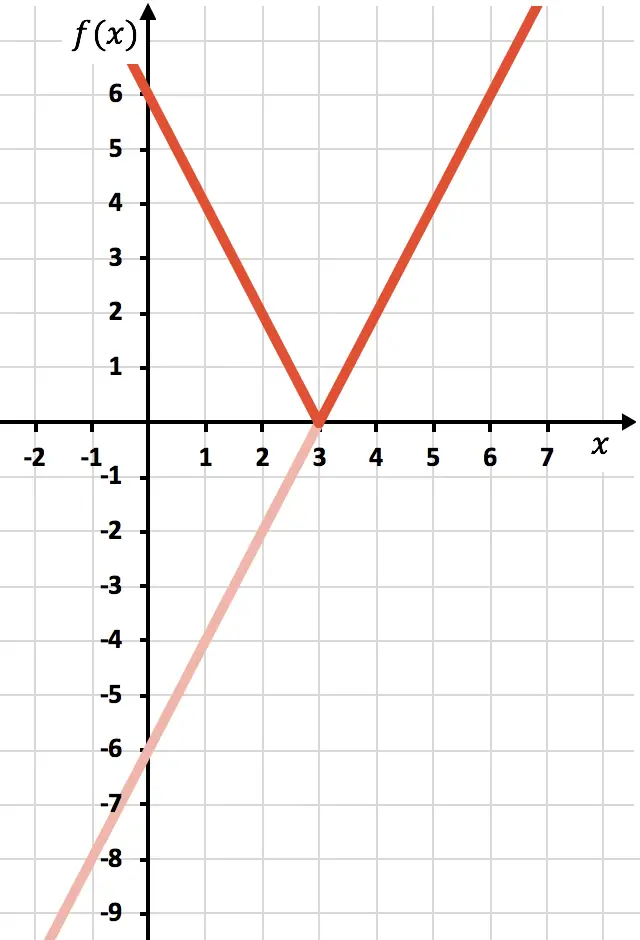
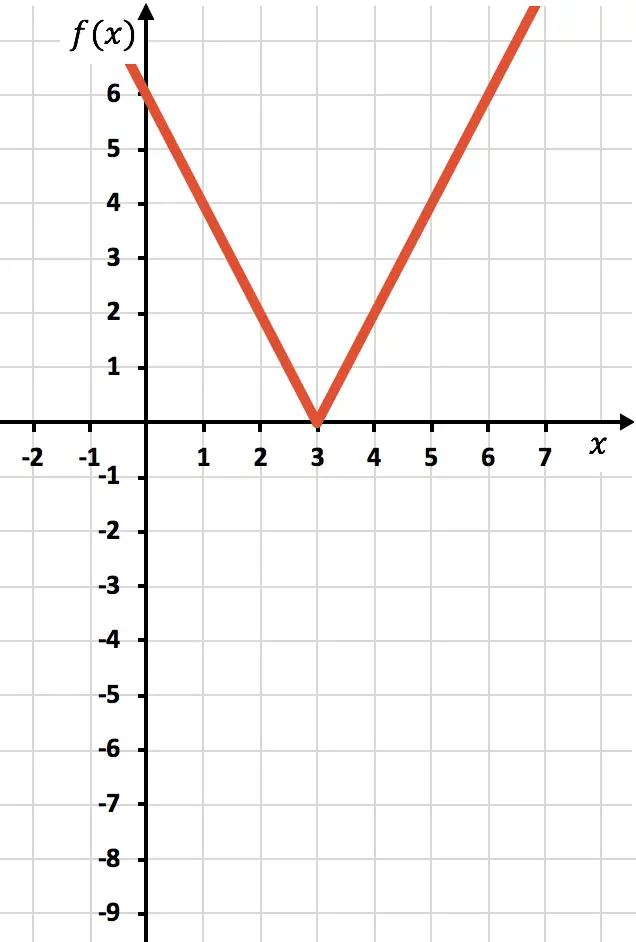
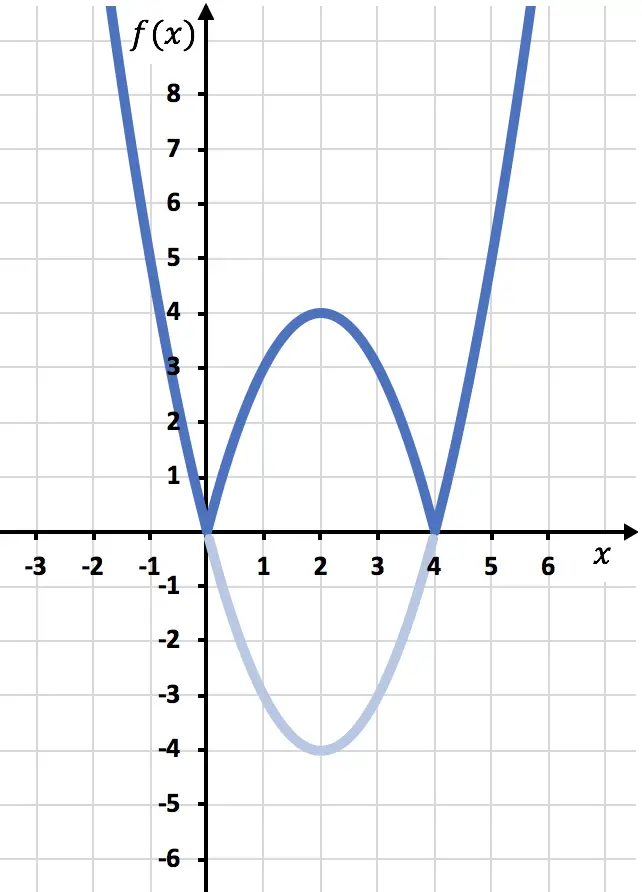
E finalmente eliminamos o traço da função que está localizada abaixo do eixo X:

como representar graficamente uma função com um valor absoluto

E desta forma já representamos a função com um valor absoluto. Como você viu, a única coisa que muda é que devemos inverter a parte da função que está localizada abaixo do eixo OX. Portanto, o gráfico de qualquer função com valor absoluto sempre estará no lado do semi-eixo Y positivo.

Por outro lado, para rever os conceitos, a partir do gráfico podemos inferir que o domínio da função de valor absoluto anterior consiste inteiramente em números reais. Por outro lado, o contradomínio ou contradomínio da referida função com valor absoluto é composto apenas por números positivos e zeros.

Exercícios resolvidos sobre funções de valor absoluto

Exercício 1

Expresse a seguinte função com um valor absoluto como uma função por partes:

$f(x)= \lvert -x+3 \rvert$

Veja a solução

Em primeiro lugar, temos que observar quando a função é negativa. Para fazer isso, igualamos o valor absoluto a zero e resolvemos a equação:

$-x+3=0$

$x=3$

Representamos o valor encontrado na linha:

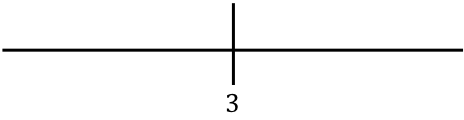
Agora avaliamos um ponto em cada intervalo da função sem o valor absoluto para descobrir qual sinal a função realmente possui em cada seção da reta:

$x<3$

Por exemplo, tomamos qualquer ponto menor que 3

$x=0:$

$-0+3$

$+3$

Positivo

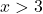$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ Por exemplo, tomamos qualquer ponto maior que 3

$x=4:$

$-4+3$

$-1$

Negativo

A função sem o valor absoluto seria negativa no intervalo x>3. Devemos, portanto, expressar a função em travessões, alterando seu sinal neste intervalo:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Exercício 2

Encontre a expressão por partes da seguinte função com um valor absoluto:

$f(x)= \lvert 3x^2-75 \rvert$

Veja a solução

A primeira coisa que precisamos fazer é determinar quando a função é negativa. Para fazer isso, precisamos definir o argumento do valor absoluto igual a zero e resolver a equação:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Representamos agora as raízes da função obtida à direita:

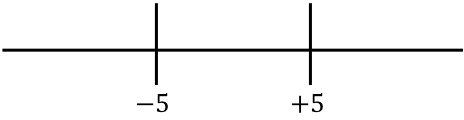
E olhamos qual sinal tem a função sem o valor absoluto em cada intervalo da reta:

$x<-5$

Por exemplo, tomamos qualquer ponto menor que -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positivo

$-5 < x < 5$

Tomamos qualquer ponto entre -5 e +5, por exemplo

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negativo

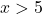$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ Por exemplo, tomamos qualquer ponto maior que 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positivo

Portanto, a função sem o valor absoluto só seria negativa no intervalo -5<x<5. Portanto, precisamos expressar a função em partes alterando apenas o sinal deste intervalo:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> 5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$

Exercício 3

Para representar uma função com valor absoluto, você deve primeiro representar a função sem valor absoluto:

É uma função afim, então é necessário construir uma tabela de valores para representá-la graficamente:

Agora precisamos desenhar a função simétrica onde a função é negativa, ou seja, onde está abaixo do eixo X. Portanto, invertemos a função de x=3 para trás:

E por fim, eliminamos a parte da função que está localizada abaixo do eixo X:

Exercício 4

Para representar uma função com valor absoluto, devemos primeiro desenhar a função sem valor absoluto.

Esta é uma função quadrática. Portanto, para representá-la, devemos calcular a coordenada X do vértice da parábola com sua fórmula:

Precisamos agora traduzir a função por simetria onde ela for negativa, ou seja, onde estiver abaixo do eixo OX. Portanto, invertemos a função de x=0 para x=4:

E finalmente excluímos a parte da função que está localizada abaixo do eixo X: