Função racional: o que é, domínio, assíntotas, gráfico, exercícios,...

Aqui você descobrirá o que são funções racionais. Além disso, explicamos como calcular o domínio e as assíntotas de uma função racional. E não só isso, mas você verá quais são todas as características das funções racionais. Finalmente, você pode praticar exercícios passo a passo sobre funções racionais.

O que é uma função racional?

A definição de uma função racional é a seguinte:

Uma função racional é uma função formada pelo quociente de dois polinômios , ou seja, uma função racional é uma fração que possui um polinômio no numerador e no denominador.

As funções racionais são caracterizadas por singularidades nos pontos onde o denominador desaparece.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Funções racionais também são chamadas de funções fracionárias.

Por outro lado, as funções racionais não devem ser confundidas com funções irracionais. Funções irracionais (ou radicais) são aquelas constituídas por raízes.

Exemplos de funções racionais

Para entender melhor a noção de função racional, veremos vários exemplos desse tipo de função.

Função racional com polinômio de primeiro grau no numerador e denominador:

$f(x)=\cfrac{x+3}{2x-5}$

Esses tipos de funções racionais também são chamadas de funções homográficas .

Função racional com constante no numerador e polinômio no denominador:

$f(x)=\cfrac{7}{x+1}$

Esses tipos de funções racionais são chamados de funções de proporcionalidade inversa e são usados para definir matematicamente quantidades inversamente proporcionais.

Função racional com um polinômio de terceiro grau no numerador e um polinômio de segundo grau no denominador:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Domínio de uma função racional

Um número dividido por 0 é uma indeterminação que dá infinito (∞), então uma função racional sempre existirá, a menos que o denominador seja 0.

Portanto, o domínio de uma função racional consiste em todos os números reais, exceto valores que cancelam o denominador.

Então, para obter o domínio de uma função racional, precisamos descobrir quando o denominador é 0, pois este ponto será o único que não pertence ao domínio

Vamos ver como o domínio de uma função racional é calculado resolvendo um exemplo:

$f(x)=\cfrac{5x}{x+2}$

Primeiro definimos o denominador igual a 0 e depois resolvemos a equação resultante:

$x+2=0$

$x=-2$

Portanto, quando x for -2, o denominador será 0 e, portanto, a função não existirá. O domínio da função, portanto, consiste em todos os números reais, exceto x=-2. Isto é afirmado da seguinte forma:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Assíntotas de uma função racional

Uma das principais propriedades das funções racionais são as suas assíntotas, pois determinam a sua representação gráfica.

➤ Veja: representação gráfica de uma função

As assíntotas de uma função racional são retas que o gráfico da função se aproxima indefinidamente, mas nunca toca.

Existem três tipos de assíntotas: assíntotas verticais, assíntotas horizontais e assíntotas oblíquas.

Abaixo você tem os três tipos de assíntotas que uma função racional pode representar graficamente em vermelho.

Assíntota vertical de uma função racional

Assíntota horizontal de uma função racional

Assíntota oblíqua de uma função racional

Como você pode ver, determinar a assíntota de uma função a partir de seu gráfico é bastante simples, mas calcular as assíntotas de uma função racional sem ter sua representação gráfica é bastante complicado. É por isso que recomendamos que você veja como as assíntotas de uma função são calculadas em nosso site.

Características de uma função racional

As funções racionais possuem as seguintes características:

$f(x)=\cfrac{P(x)}{Q(x)}$

Como vimos acima, o domínio das funções racionais inclui todos os números reais exceto valores que anulam o denominador da fração.

Em geral, o contradomínio (ou contradomínio) de uma função racional inclui todos os números reais, exceto valores em que a função possui uma assíntota horizontal.

As funções racionais são contínuas em todo o seu domínio. Ou seja, as funções racionais apresentam descontinuidades em pontos que não pertencem ao seu domínio.

A representação gráfica da maioria das funções racionais consiste em duas hipérboles.

Algumas regras para as assíntotas de funções racionais podem ser deduzidas do numerador polinomial.
$P(x)$

e o polinômio denominador

$Q(x):$
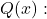
- Uma função racional tem uma assíntota vertical nos pontos que são as raízes de
  $Q(x)$
  
  mas estas não são raízes de
  
  $P(x).$
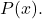
- Se o grau de
  $P(x)$
  
  é menor que o grau de
  
  $Q(x)$
  
  , a reta y=0 é uma assíntota horizontal da função racional.
- Se o grau de
  $P(x)$
  
  é maior que o grau de
  
  $Q(x)$
  
  , a função racional não tem assíntota horizontal.
- Se o grau de
  $P(x)$
  
  é uma unidade maior que o grau de
  
  $Q(x)$
  
  e os dois polinômios não têm raiz comum, a função racional tem uma assíntota oblíqua.

Exercícios resolvidos sobre funções racionais

Exercício 1

Encontre o domínio da seguinte função racional:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Veja a solução

É uma função racional, então o domínio consiste em todos os números exceto aqueles que cancelam o denominador, porque então a função daria ∞.

Então definimos o denominador inteiro igual a zero para ver qual número não pertence ao domínio:

$2x+4=0$

E resolvemos a equação resultante:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

O domínio da função é, portanto, composto apenas por números, exceto -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Exercício 2

Encontre os pontos de corte da seguinte função racional com os eixos cartesianos:

$f(x)=\cfrac{x^2-9}{x}$

Veja a solução

Ponto de corte com eixo X

Para encontrar o ponto de intersecção da função com o eixo X é necessário resolver

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

Obtivemos duas soluções da equação quadrática, portanto a função racional intercepta o eixo das abcissas em dois pontos diferentes, que são:

$\bm{(3,0)\qquad (-3,0)}$

Ponto de corte com eixo Y

Para encontrar o ponto de intersecção com o eixo Y você deve calcular

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Qualquer número dividido por zero é uma indeterminação que dá infinito. Portanto, a função racional não passa em nenhum ponto acima do eixo Y, ou seja, não possui ponto de intersecção com o eixo y.

Exercício 3

Trace a seguinte função racional em um gráfico:

$y=\cfrac{2x+3}{2x+6}$

Veja a solução

A primeira coisa a fazer é calcular o domínio da função:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Depois de conhecermos o domínio da função, construímos uma tabela de valores:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Para finalizar, basta representar os pontos obtidos em um gráfico e desenhar as hipérboles, desenhando assim a função racional:

Exercício 4

Determine as assíntotas da função racional representada graficamente abaixo:

Veja a solução

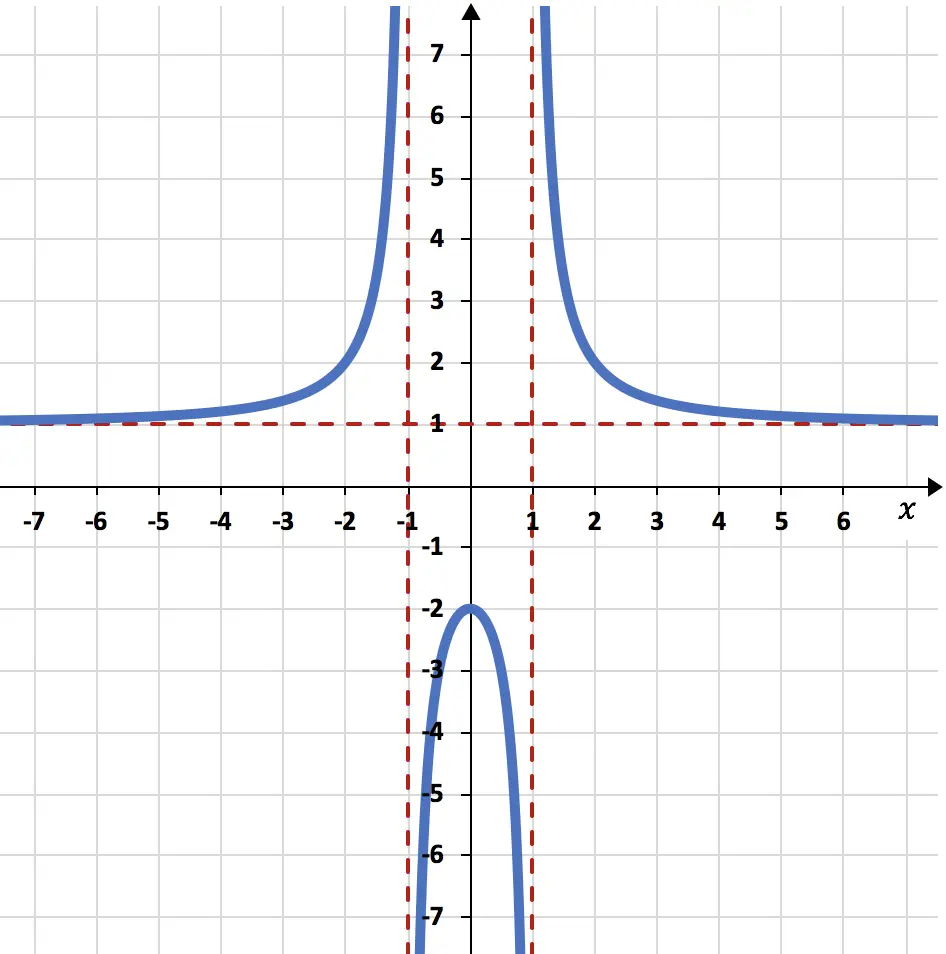
As assíntotas são claramente visíveis no gráfico, pois são representadas como linhas pontilhadas vermelhas.

Neste problema, a função está muito próxima da linha horizontal y=1, mas nunca a toca. Portanto, a função racional possui uma única assíntota horizontal, que é y=1.

Da mesma forma, a representação gráfica da função está muito próxima das linhas verticais x=-1 e x=1, mas nunca atinge estes valores. A função racional, portanto, tem duas assíntotas verticais diferentes, que são x=-1 e x=1.

Exercício 5

Calcule todas as assíntotas da seguinte função racional:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Nota: Para resolver este exercício, recomendamos que você primeiro acesse o link acima sobre como são calculadas as assíntotas de uma função e veja a explicação.

Veja a solução

assíntota vertical

Para calcular as assíntotas verticais de uma função, devemos primeiro encontrar o domínio da função. Portanto, igualamos o denominador da função racional a 0 para encontrar os pontos que não pertencem ao domínio:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

O domínio da função, portanto, consiste em todos os números, exceto -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Então x=-1 poderia ser uma assíntota vertical. Para verificar isso, devemos calcular o limite da função no ponto:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Portanto, x=-1 é uma assíntota vertical da função racional, já que o limite da função neste ponto dá infinito.

assíntota horizontal

Para determinar as assíntotas horizontais, precisamos calcular o limite infinito da função:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

Nesse caso, o resultado do limite infinito indeterminado entre o infinito é a divisão dos coeficientes do x de maior grau, pois o numerador e o denominador são da mesma ordem.

Os dois limites infinitos da função nos deram 3, então y=3 é uma assíntota horizontal da função racional.

assíntota oblíqua

Como existe uma assíntota horizontal, a função racional não possui uma assíntota oblíqua.

O que é uma função racional?

Exemplos de funções racionais

Domínio de uma função racional

Assíntotas de uma função racional

Características de uma função racional

Exercícios resolvidos sobre funções racionais

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta