Função polinomial

Aqui você encontrará o que são funções polinomiais e o que são todos os tipos de funções polinomiais. Além disso, também explicamos as propriedades das funções polinomiais.

O que é uma função polinomial?

Uma função polinomial é uma função cuja expressão algébrica é um polinômio , ou seja, uma função polinomial é definida pela adição ou subtração de um número finito de termos de diferentes graus.

Portanto, uma função polinomial é descrita matematicamente pela seguinte expressão:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Por outro lado, funções polinomiais também podem ser definidas usando a seguinte fórmula:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

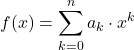
onde os termos

$a_k$

$x^k$

são respectivamente o coeficiente e a variável de cada monômio que forma a função polinomial.

O termo

$a_nx^n$

, denominado termo principal, indica o grau da função polinomial, pois é o monômio de maior grau da função. Em outras palavras, o expoente de maior valor é aquele que indica o grau da função polinomial.

Embora veremos mais características das funções polinomiais abaixo, o domínio de qualquer função polinomial são todos números reais.

Tipos de funções polinomiais

Dada a definição de função polinomial, veremos agora quais são todos os tipos de funções polinomiais que existem.

função constante

A função constante é uma função polinomial de grau 0, portanto é um tipo de função que sempre assume a mesma imagem para qualquer valor da variável independente (x).

A expressão geral para a função constante é a seguinte:

$f(x)=k$

Por exemplo, as três funções a seguir são constantes ou funções polinomiais de grau zero:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

A representação gráfica de uma função constante é uma linha horizontal (paralela ao eixo x) com valor igual à constante.

Você pode ver mais recursos sobre este tipo de função no seguinte link:

➤ Veja: características da função constante

Função linear

Uma função linear , também chamada de função afim, é uma função polinomial de primeiro grau. Assim, uma função polinomial deste tipo só pode ser composta por um termo linear e um termo independente:

$f(x)=mx+n$

Ouro

$m$

é a inclinação da linha e

$n$

é a interceptação y, ou seja, onde a função cruza o eixo Y.

Exemplos de funções lineares ou funções polinomiais de primeiro grau:

$f(x)=4x+3\qquad f(x)=-5x$

Alguns distinguem a função linear da função afim dependendo se a função tem como termo

$n$

ou não, sendo a função afim com o intercepto e a função linear sem.

A representação gráfica das funções lineares são sempre retas cujo grau de inclinação depende do valor da inclinação da função.

Abaixo você pode ver graficamente a função polinomial de primeiro grau

$f(x)=2x-1.$

No entanto, para representar graficamente uma função linear, você precisa ter clareza sobre vários conceitos. No link a seguir você encontrará a explicação passo a passo de como representar graficamente uma função polinomial deste tipo:

➤ Veja: Representação gráfica de uma função linear

Função quadrática

Uma função quadrática é uma função polinomial de grau 2, ou seja, uma função cujo termo de grau superior é de segundo grau.

Portanto, a fórmula para uma função quadrática é:

$f(x)=ax^2+bx+c$

Ouro

$ax^2$

é o termo quadrático,

$bx$

o termo linear e

$c$

o termo independente da função polinomial.

Exemplos de funções quadráticas ou funções polinomiais quadráticas:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

O gráfico de uma função quadrática é sempre uma parábola e sua forma depende do sinal do coeficiente líder.

$a:$

Se o coeficiente
$a$

é positiva, a função quadrática é convexa (em forma

$\bm{\cup}$

).
Em vez disso, se o coeficiente
$a$

é negativo, a função quadrática é côncava (em forma

$\bm{\cap}$

).

Assim, com o sinal do coeficiente principal da função polinomial quadrática, podemos saber a forma que seu gráfico assumirá, mas para fazer sua representação gráfica exata deve ser seguido um procedimento específico. Você pode ver este procedimento no seguinte link:

➤ Veja: Representação gráfica de uma função quadrática

função cúbica

Uma função cúbica é uma função polinomial de terceiro grau. Portanto, este tipo de funções polinomiais é expresso algebricamente da seguinte forma:

$f(x)=ax^3+bx^2+cx+d$

Exemplos de funções cúbicas ou funções polinomiais de terceiro grau:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

As representações gráficas de funções cúbicas correspondem a curvas cúbicas. Porém, para representar este tipo de funções em um gráfico, deve-se seguir um procedimento complicado (inclui derivadas). Você pode ver como isso é feito aqui:

➤ Veja: Como representar uma função

Como você pode ver, os tipos de funções polinomiais são na verdade infinitos, pois um polinômio pode ter termos infinitos. Assim, por exemplo, uma função quártica é como uma função cúbica, mas com a adição de um termo quadrático. O importante é você entender que o tipo de função polinomial é marcado pelo grau da função.

Propriedades de funções polinomiais

As funções polinomiais têm as seguintes características:

O domínio de qualquer função polinomial é o conjunto dos números reais.

$\text{Dom } f=\mathbbf{R}$

Todas as funções polinomiais são contínuas.

Funções polinomiais de grau maior que 1 não possuem assíntotas.

Independentemente do tipo de função polinomial, o único ponto de intersecção com o eixo das ordenadas (eixo Y) está na altura do seu termo independente, ou seja, no seguinte ponto:

$(0,a_0)$

Por outro lado, uma função polinomial intercepta o eixo das abcissas (eixo X), no máximo, tantas vezes quanto o grau da função.

Se uma função polinomial tiver apenas termos de grau par, isso implica que ela é simétrica em relação ao eixo OY. Por outro lado, se uma função polinomial possui apenas termos de grau ímpar, isso significa que a função é simétrica em relação à origem das coordenadas.

O número de extremos relativos (máximo ou mínimo) de uma função polinomial é, no máximo, o grau do polinômio da função menos 1.

O número de pontos de inflexão de uma função polinomial é no máximo igual ao grau do polinômio da função menos 2.

As operações podem ser realizadas com funções polinomiais:
- A soma de duas funções polinomiais dá outra função polinomial.
- O produto de duas funções polinomiais dá origem a outra função polinomial.
- Multiplicar uma função polinomial por um escalar (número real) resulta em uma função polinomial semelhante, mas com seu gráfico reduzido ou expandido.
- A composição de duas funções polinomiais é igual a outra função polinomial.