Função linear e função afim -

Neste artigo você encontrará a explicação da função afim e da função linear, bem como as diferenças que existem entre esses dois tipos de funções. Além disso, você verá exemplos de como representar graficamente uma função afim e uma função linear e como calcular suas expressões a partir de dois pontos. Por fim, você poderá treinar com diversos exercícios resolvidos passo a passo.

O que é uma função afim e uma função linear?

As definições da função afim e da função linear são as seguintes:

Uma função afim é uma função polinomial de primeiro grau, ou seja, uma função que, representada no gráfico, é uma reta. As funções associadas são as seguintes:

$f(x)=mx+n$

Ouro

$m$

é a inclinação da linha e

$n$

Esta é a interceptação y, ou seja, onde a função intercepta o eixo vertical.

Em matemática, as funções afins também são chamadas de transformações lineares no contexto da álgebra linear.

Uma função linear é uma função afim que não possui um termo independente. Portanto, a fórmula para funções lineares é:

$f(x)=mx$

Ouro

$m$

é a inclinação da linha.

O domínio e o contradomínio (ou contradomínio) da função linear e da função afim são todos números reais:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Qual é a diferença entre uma função linear e uma função afim?

Agora que você viu os conceitos de função linear e função afim, deve ter notado que eles são muito semelhantes entre si. No entanto, a seguinte diferença entre eles é muito importante:

A única diferença entre a função linear e a função afim é que a função linear não possui um termo independente enquanto a função afim sempre possui o coeficiente de interceptação (n) diferente de zero (0).

Função linear

$f(x)=mx$

Função linear

$f(x)=mx+n$

Isso implica que uma função linear sempre passa pela origem da coordenada , o ponto (0,0). Por outro lado, uma função afim nunca passará por este ponto porque possui um intercepto diferente de 0.

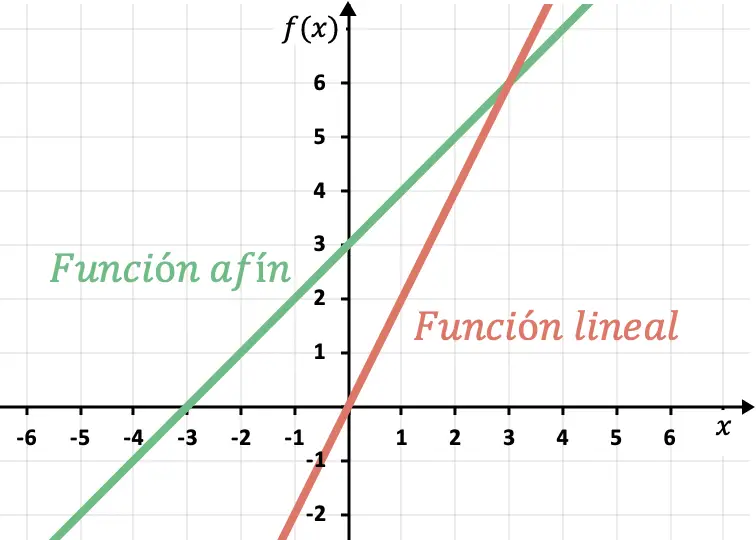
Qual é a diferença entre uma função linear e uma função afim?

Inclinação e interceptação y de uma função linear ou afim

Nesta seção, analisaremos um exemplo de função afim ou linear para entender o significado dos termos

$m$

$n$

, ou em outras palavras, a inclinação e a interceptação y.

Determine a expressão para a função mostrada no gráfico e classifique-a como linear ou afim.

Esses tipos de funções seguem a seguinte expressão:

$f(x)=mx+n$

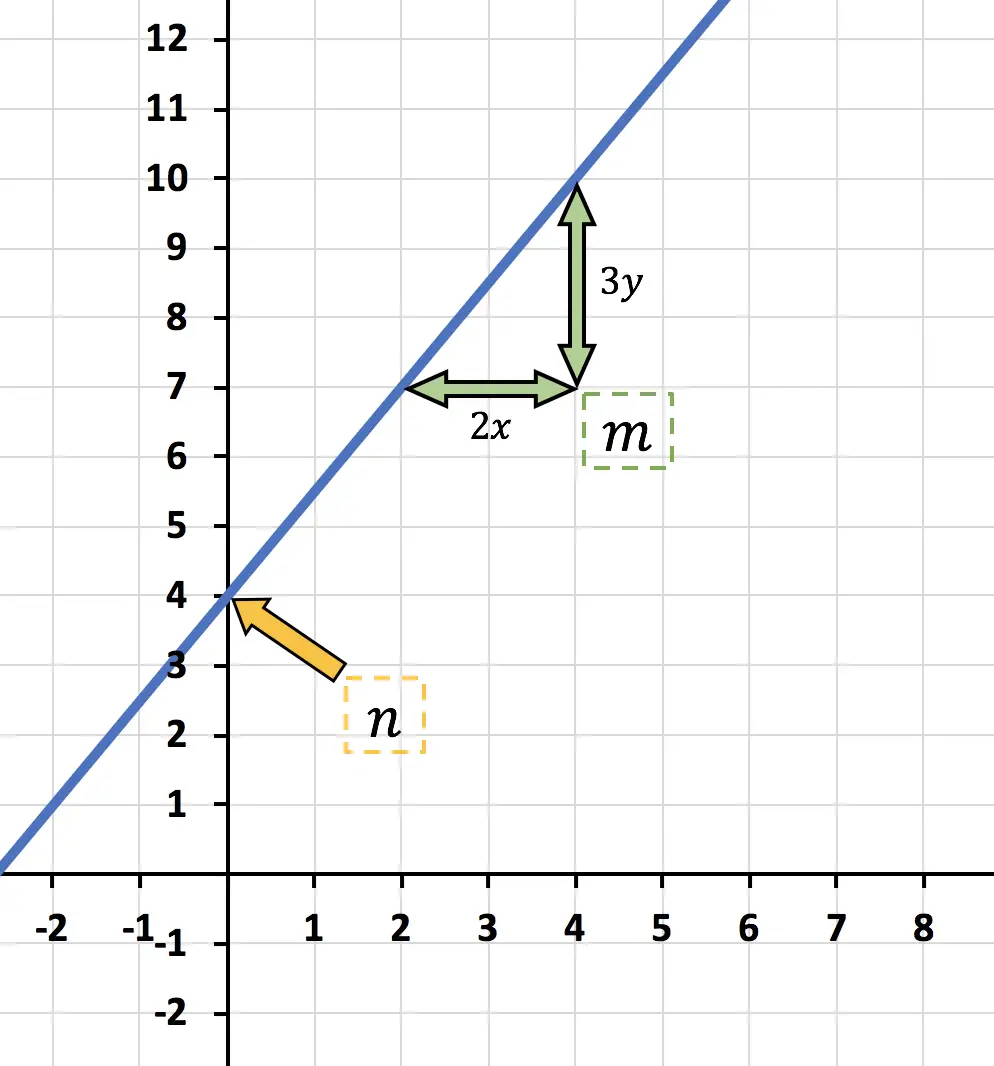
significando inclinação e função linear ou afim de interceptação y m e n

$n$

Esta é a interceptação y, ou seja, onde a função intercepta o eixo Y vertical. Então, neste caso:

$n=4$

Do outro lado,

$m$

é a inclinação da linha. Y pode ser calculado dividindo a diferença em y entre dois pontos pela diferença em x entre esses mesmos dois pontos:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

diz “quanto y aumenta para cada x” , então neste caso a função “3y aumenta para cada 2x” .

Concluindo, a expressão para a função afim representada no gráfico é:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

Além disso, como a interceptação y é diferente de zero, é uma função afim .

Abaixo mostramos mais exemplos de funções lineares e afins para completar seu entendimento:

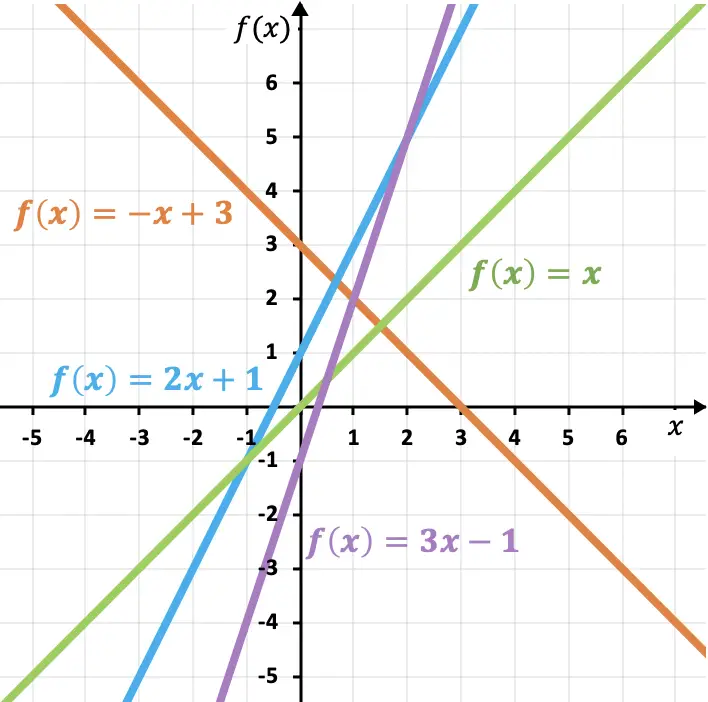
Como você pode ver nestes exemplos, quanto maior a inclinação, mais íngreme será a reta e, portanto, maior será a função. Da mesma forma, o coeficiente de inclinação determina o crescimento ou diminuição de uma função:

Se a inclinação for positiva, a função é crescente , ou seja, aumenta à medida que x aumenta.
Se a inclinação for negativa, a função é decrescente , ou seja, diminui à medida que x aumenta.

Além disso, você também pode saber se duas retas são paralelas ou perpendiculares por suas inclinações:

Quando duas retas têm a mesma inclinação, elas são paralelas , ou seja, não se cruzam em nenhum ponto ou são completamente idênticas.

$m_1 = m_2$

Por outro lado, duas retas são perpendiculares , ou seja, se cruzam num ângulo vertical (90º), se suas inclinações corresponderem à seguinte relação:

$m_1 = -\cfrac{1}{m_2}$

Exemplo de representação de uma função afim ou linear

Vamos ver como representar graficamente uma função de primeiro grau usando um exemplo.

Faça um gráfico da seguinte função afim:

$f(x)=2x-1$

A primeira coisa que precisamos fazer é criar um array de valores. Para fazer isso, concedemos os valores que queremos

$x$

para obter valores de

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

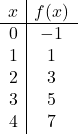
Embora uma tabela de valores com dois pontos seja suficiente, podemos fazer mais pontos para ter certeza de que está correta.

Depois de criar a tabela de valores, plotamos os pontos no gráfico:

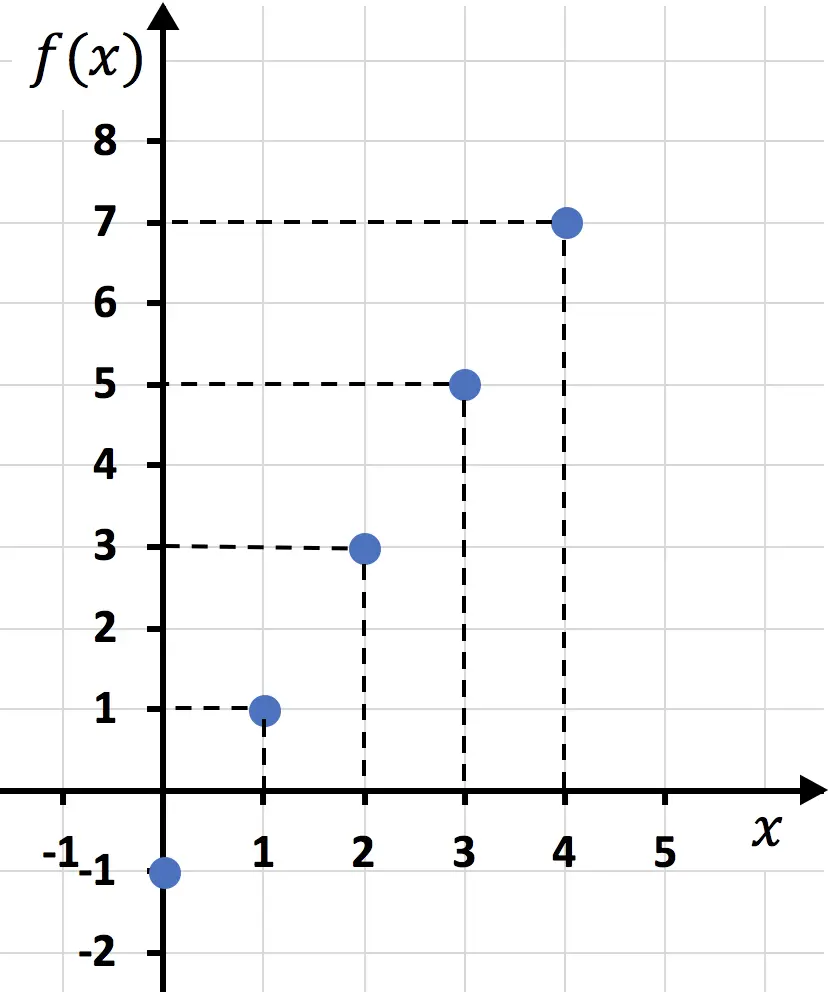
como representar uma linha ou uma função linear ou e afim

E finalmente, juntamos os pontos e traçamos uma linha:

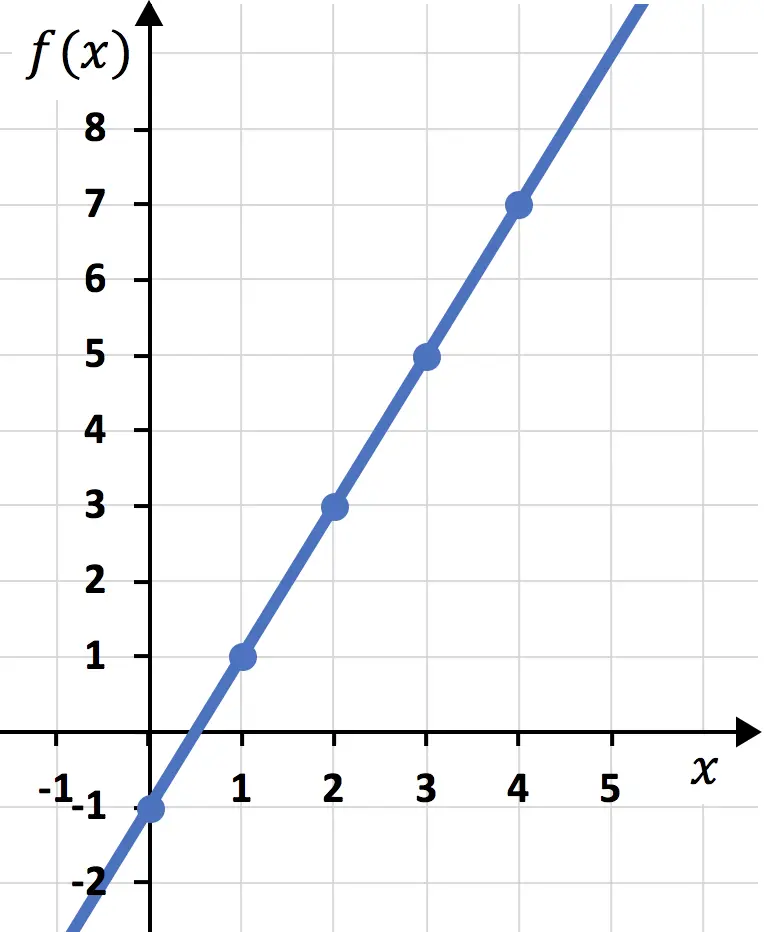
representação gráfica de uma função linear ou afim

E desta forma, já representamos a função num gráfico. Como você pode ver, não é complicado, basta primeiro fazer uma tabela de valores e depois traçar os pontos em um gráfico.

Como calcular uma função linear ou afim de dois pontos

Agora vamos ver como encontrar uma função linear ou afim de dois pontos usando um exemplo:

Calcule a função linear que satisfaz
$f(3)=5$

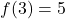
e passar pelo ponto

$(1,-1).$

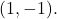
Em primeiro lugar,

$f(3)=5$

Isso significa que a função passa pelo ponto

$(3,5)$

Portanto, como temos dois pontos pelos quais a função passa, podemos calcular a inclinação

$m$

função:

Considerando dois pontos,

$P_1=(x_1,y_1)$

$P_2=(x_2,y_2)$

, declive

$m$

da função é calculada:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

No nosso caso a função passa pelos pontos

$(3,5)$

$(1,-1)$

. Então a inclinação

$m$

da função é:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

A função será, portanto, da forma:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Uma vez que sabemos

$m$

podemos resolver o mistério

$n$

. Para fazer isso, substituímos as coordenadas de um ponto pertencente à função na equação. Por exemplo, ponto (3.5):

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

Resolvemos a equação resultante:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

A função linear é, portanto:

$\bm{f(x)=3x-4}$

Exercícios resolvidos sobre funções lineares e afins

Exercício 1

Determine a inclinação e a origem da seguinte função afim:

$f(x)=-5x-2$

Veja a solução

Uma função linear tem a forma

$f(x)=mx+n .$

A inclinação da função é portanto o número que acompanha x , que neste caso é -5:

$\bm{m=-5}$

E a interceptação y é o termo independente, que neste caso é -2:

$\bm{n=-2}$

Exercício 2

Faça um gráfico da seguinte função afim:

$f(x)=x+1$

Veja a solução

Primeiro damos valores para

$x$

para criar a tabela de valores:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

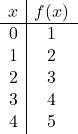
E então representamos os pontos da tabela de valores no gráfico e traçamos a reta:

Exercício 3

Trace a seguinte função afim no gráfico:

$f(x)=-2x+6$

Veja a solução

Primeiro damos valores para

$x$

para criar a tabela de valores:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

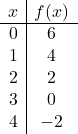
E por fim representamos os pontos da tabela de valores no gráfico e traçamos a reta:

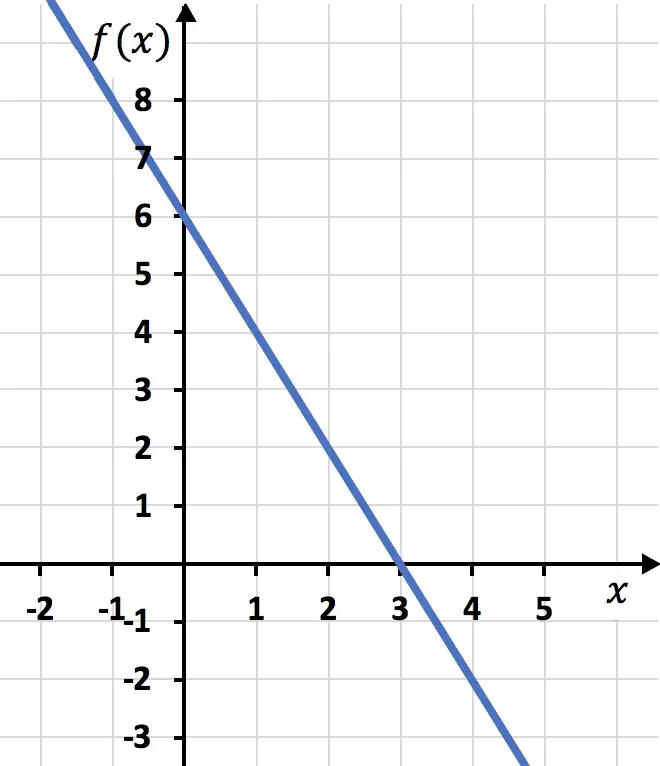
exercício resolvido passo a passo de função linear e afim

Exercício 4

Encontre a expressão para a função afim que passa pelos pontos (2,3) e (0,1).

Veja a solução

A função passa pelos pontos (2,3) e (0,1), então a inclinação da função é:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

E a função terá a forma:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Depois de conhecermos m, podemos calcular n . Para fazer isso, precisamos substituir as coordenadas de um ponto pertencente à função na equação. Por exemplo, ponto (2,3):

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

Devemos agora resolver a equação resultante:

$3-2=n$

$1 = n$

A função, portanto, corresponde à seguinte expressão:

$\bm{f(x)=x+1}$

Exercício 5

Faça um gráfico da seguinte função afim:

$f(x)=2x-1$

Veja a solução

Primeiro damos valores para

$x$

para criar a tabela de valores:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

E então representamos os pontos da tabela de valores no gráfico e traçamos a reta:

Exercícios resolvidos para representar graficamente uma função linear ou afim

Exercício 6

Calcule a função linear que satisfaz as duas condições a seguir:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Veja a solução

Que isso se torne realidade

$f(3)=-2$

Isso significa que a função passa pelo ponto (3,-2). E, da mesma forma,

$f(-1)=6$

Isso significa que a função passa pelo ponto (-1,6).

Então a função passa pelos pontos (3,-2) e (-1,6), então sua inclinação é:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

A função será, portanto, da forma:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

E uma vez que conhecemos m, podemos calcular n . Para fazer isso, substituímos na equação as coordenadas de um ponto que pertence à função. Por exemplo, o ponto (3,-2):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

E resolvemos a equação resultante:

$-2=-6+n$

$-2+6=n$

$4 = n$

A função é portanto:

$\bm{f(x)=-2x+4}$

Exercício 7

Encontre a função afim que ela executa

$f(1) =6$

e passa pelo ponto (3.5).

Veja a solução

Que isso se torne realidade

$f(1)=6$

Isso significa que a função passa pelo ponto (1,6).

A função passa portanto pelos pontos (1.6) e (3.5) e portanto o seu declive é:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

A função será, portanto, da forma:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

Depois de conhecermos o termo m, podemos calcular o coeficiente n . Para fazer isso, substituímos na equação as coordenadas de um ponto que pertence à função. Por exemplo, o ponto (1,6):

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

Resolvemos a equação resultante:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

Lembre-se que para somar frações, primeiro você deve reduzi-las a um denominador comum e depois somar os numeradores:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

A função é portanto:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Exercício 8

Resolva o seguinte problema relacionado a funções lineares e afins:

Uma loja vende 40 unidades de um produto quando o preço é 15€/unidade e 65 unidades quando o preço é 10€/unidade.

Calcule a função de demanda do produto, assumindo que é uma função afim.
Quantas unidades serão vendidas se o preço for fixado em 12€/unidade?

Veja a solução

Por ser uma função afim, a função será do tipo

$f(x)=mx+n .$

Ouro

$x$

será o preço unitário do produto e

$f(x)$

serão as unidades vendidas.

O comunicado diz-nos que quando o preço é de 15€/unidade, são vendidas 40 unidades. Portanto, como

$x$

é o preço e

$f(x)$

unidades vendidas, deverá ser respeitada a seguinte igualdade:

$f(15)=40$

E quando o preço é de 10€/unidade, são vendidas 65 unidades. Então, usando o mesmo raciocínio:

$f(10)=65$

Que isso se torne realidade

$f(15)=40$

Isso significa que a função passa pelo ponto (15.40). E

$f(10)=65$

Isso significa que a função passa pelo ponto (10,65).

A inclinação da função é, portanto:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

A função será, portanto, da forma:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

Depois de conhecermos m, podemos calcular n . Para fazer isso, substituímos na equação as coordenadas de um ponto que pertence à função. Por exemplo o ponto (15h40):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$