Neste artigo explicamos o que é uma função inversa (ou recíproca) e como calcular a inversa de uma função. Você também descobrirá como saber facilmente se uma função tem inversa ou não e as propriedades desse tipo de função. Finalmente, você pode praticar exercícios passo a passo sobre funções inversas.
Qual é a função inversa?
A função inversa, também chamada de função recíproca, é a função cujo domínio é o contradomínio de outra função (a função original) e cujo contradomínio é o domínio da função original. A função inversa da função f é expressa com o símbolo f -1 .
Portanto, a função inversa de f(x) é a função que satisfaz a seguinte condição:
Ouro
![]()
é a função inversa de
![]()
O conceito de função inversa também pode ser definido usando composição de funções, pois qualquer função composta com sua função inversa é igual à função identidade:
![]()
➤ Veja: o que é composição de funções?
Portanto, se a equação anterior for satisfeita, significa que
![]()
é a função inversa (ou função recíproca) de
![]()
Exemplo de função inversa
Dada a definição de função inversa, vamos resolver um exemplo para entender melhor seu significado.
- Determine se as seguintes funções são inversas uma da outra:
![]()
Se as duas funções forem inversas uma da outra, as 2 condições a seguir serão atendidas:
![]()
Então, vamos verificar se ambas as equações estão satisfeitas. Nós primeiro verificamos
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7d5f4d815a58f808114ae471c31dd_l3.png)
➤ Se você não entendeu o cálculo que acabamos de fazer, você precisa acessar o link acima para Qual é a composição das funções? , explicamos como resolver este tipo de operação com funções.
Para que
![]()
sim, está realizado. ✅
Agora vamos verificar a igualdade
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83423fe7deab472f1a7e9575ec7af8c4_l3.png)
E a condição de invertibilidade
![]()
também é realizado. ✅
Concluindo, como ambas as equações são válidas, as duas funções são inversas uma da outra.
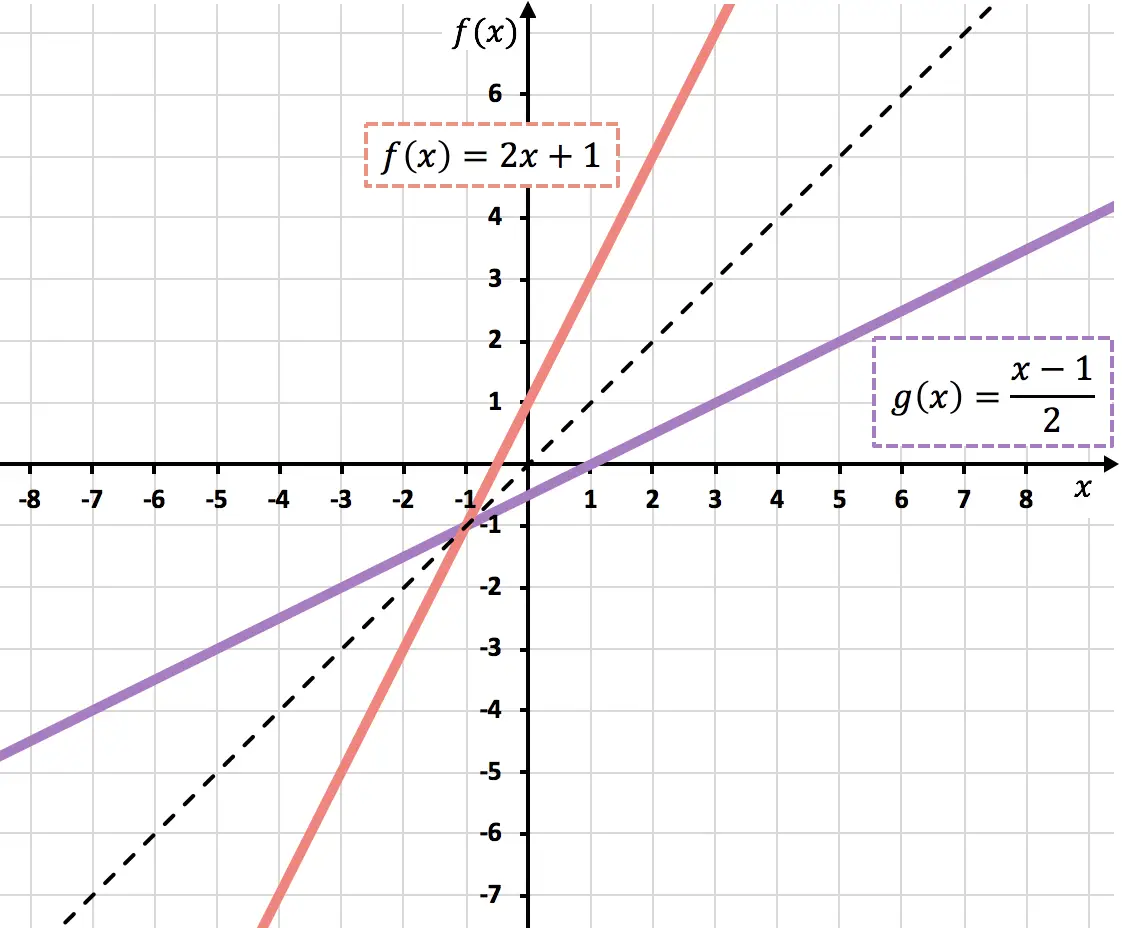
Abaixo você pode ver ambas as funções representadas graficamente. Observe que os gráficos de duas funções inversas são simétricos em relação à bissetriz do primeiro e terceiro quadrantes:
Como saber se uma função tem inversa
Uma função tem função inversa se for uma função injetiva , ou seja, se cada valor em todo o seu domínio corresponder a um único valor no seu intervalo.
Função exponencial com função inversa

Função quadrática sem função inversa

Por exemplo, a função exponencial esquerda tem uma função inversa porque cada x corresponde a um único valor de f(x) . Por outro lado, a função quadrática direita não possui função inversa pois possui vários valores de x cujas imagens são iguais (por exemplo f(1)=f(3)=2) .
Da mesma forma, uma função bijetiva consiste em uma função que é injetiva e sobrejetiva, portanto, qualquer função bijetiva também possui uma função inversa.
Por outro lado, você deve ter em mente que a função inversa não é a mesma coisa que a inversa multiplicativa de uma função , mas sim dois conceitos diferentes. Para encontrar o inverso multiplicativo de uma função, basta calcular 1 correspondência por essa função.
![]()
Na próxima seção veremos como determinar a função inversa.
Como encontrar a função inversa
Para calcular o inverso de uma função, as seguintes etapas devem ser executadas:
- Substitua f(x) por y .
- Mude tudo x para y e vice-versa.
- Limpe a variável y .
- Substitua a variável y por f -1 (x) . A função inversa é a expressão encontrada para f -1 (x) .
Para que você possa ver exatamente como a função inversa é calculada, determinaremos a inversa da seguinte função como exemplo:
![]()
Primeiro de tudo, precisamos substituir
![]()
Para
![]()
:
![]()
Agora vamos mudar tudo
![]()
da função por
![]()
, e vice versa:
![]()
Então limpamos a variável
![]()
![]()
![]()
![]()
![]()
E finalmente, a função inversa de
![]()
é a expressão algébrica que obtivemos isolando
![]()
![]()
Exercícios resolvidos da função inversa
Abaixo preparamos vários exercícios passo a passo sobre a função inversa para que você possa praticar.
👉 Lembre-se que se você não entende como resolver um exercício ou quer que resolvamos um problema para você, pode nos escrever nos comentários!
Exercício 1
Verifique se as duas funções a seguir são inversas (ou recíprocas) ou não:
![]()
Para que as duas funções sejam inversas uma da outra, o seguinte deve ser verdadeiro:
![]()
É portanto necessário verificar se as duas condições estão preenchidas. Nós primeiro verificamos
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbbdf5bb2c308a1973c5f2d99e822ad5_l3.png)
Ainda,
![]()
sim, está realizado. ✅
Agora vamos verificar a outra composição de funções
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5819584c8358b812c8214a902e4f08_l3.png)
Através do qual
![]()
também é realizado. ✅
Como é que isso acontece
![]()
e
![]()
, as duas funções são inversas uma da outra.
Exercício 2
Calcule a função inversa (ou recíproca) da seguinte função polinomial de primeiro grau:
![]()
A primeira coisa a fazer para inverter a função é substituir o termo
![]()
Para
![]()
![]()
Agora mudamos o
![]()
por
![]()
, e vice versa:
![]()
E então liberamos
![]()
![]()
![]()
![]()
![]()
Já conseguimos liberar
![]()
. Portanto, a função inversa de
![]()
Leste:
![]()
Exercício 3
Inverta a seguinte função polinomial quadrática:
![]()
Para encontrar a função inversa seguiremos o procedimento que vimos acima. Então vamos ligar
![]()
para a função
![]()
![]()
Em segundo lugar, modificamos o
![]()
para o
![]()
, e vice versa:
![]()
E finalmente isolamos a variável
![]()
![]()
![]()
![]()
![]()
Porém, neste caso a função obtida possui duas imagens para cada elemento do seu domínio (a imagem positiva e a imagem negativa). Portanto, não existe função inversa da função problema.
Exercício 4
Determine a função inversa (ou função recíproca) da seguinte função racional:
![]()
Primeiro, substituímos
![]()
Para
![]()
![]()
Agora mudamos o
![]()
numerador e denominador
![]()
, e vice versa:
![]()
E então liberamos
![]()
![]()
A expressão
![]()
divide todo o lado direito da equação, então podemos multiplicá-lo multiplicando todo o lado esquerdo da equação:
![]()
![]()
Colocamos todos os termos com
![]()
de um lado da equação e os outros termos do outro lado:
![]()
Para limpar
![]()
, extraímos o fator comum do lado esquerdo da equação:
![]()
E como carteiro
![]()
é multiplicar todo o lado esquerdo da equação, podemos fazer isso dividindo todo o lado direito:
![]()
Já conseguimos liberar
![]()
. Então a função inversa de
![]()
Leste:
![]()
Propriedades da função inversa
A função inversa tem as seguintes características:
- A função inversa é única, ou seja, se uma função é invertível, para esta função existe apenas uma função inversa.
- O domínio da função inversa é o contradomínio (ou contradomínio) da função original.
- Da mesma forma, o caminho da função inversa é equivalente ao domínio da função original.
- Qualquer função composta por sua função inversa fornece a função identidade (x).
![]()
- O gráfico de uma função e o gráfico de sua função inversa são simétricos em relação à bissetriz do primeiro e terceiro quadrantes.
- O inverso da função inversa é igual à função original:
![]()
- Inverter uma função composta equivale a calcular o inverso de cada função separadamente e depois compor as funções inversas.
![]()
- Uma função é simultaneamente contínua com a sua função inversa, ou seja, se uma função é contínua, a sua função inversa também o será.
- Se uma função é diferenciável e a derivada não desaparece em nenhum momento
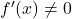
, sua função inversa também será diferenciável.
Adicionalmente, a derivada da função inversa pode ser calculada aplicando o teorema da função inversa , cuja fórmula é:
![]()